1.1 Методичний приклад

Нехай передавальною функцією об’єкту керування є .

Необхідно знайти стабілізуючий регулятор K(s). Для розв’язку завдання виконуємо послідовно алгоритм Евкліда.

1. .

2.

= ∙ +

3.

= ∙ +

4.

= ∙

5.

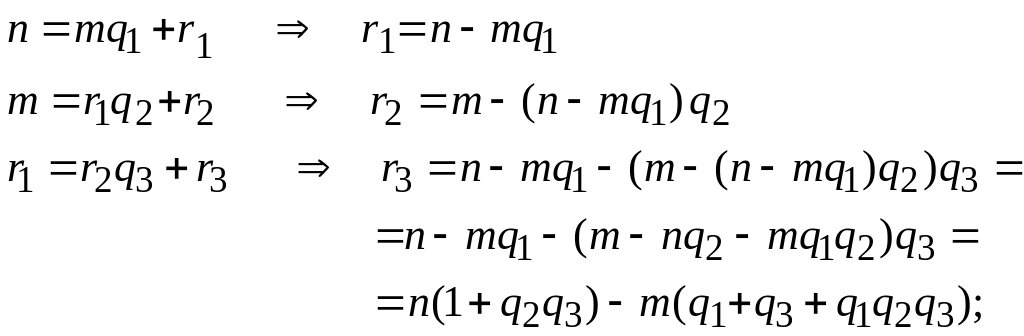
6 .

7. В отримані таким чином і підставимо . В даному прикладі передавальна функція стабілізуючого регулятору для Q(s) = 0 визначається наступною формулою:

.

Перехідний процес в замкненої системі при одиничному задавальному діянні наведено на рис. 3.

Рисунок 3 – Перехідний процес у замкненої системи з регулятором

2. Завдання

Для заданого варіанту нестійкої передавальної функції об’єкту керування розрахувати стабілізуючий регулятор K(s) і шляхом підбору параметру Q(s) забезпечити добру якість замкненої системи керування (наприклад, перерегулювання не повинно перевищувати 20–40%).

Таблиця 1 – Таблиця варіантів

№ варіанту	Передавальна функція
1	G(s) = 120/s2
2	G(s) = 100/(s3 +s2 )
3	G(s) = 5/(10s3 - 3s2 - s)
4	G(s) = 2,5(s – 2)/(10s2-3s-1)
5	G(s) = 0,5(s-0,5)/(5s2 – 9s - 2)
6	G(s) = 20/(4s3-s)
7	G(s) = 1/(s3 – 2s2 + 2s)
8	G(s) = 40/(s3 – 3s2 + 3,25s)
9	G(s) = 5(2s – 1)/ (s2 – 3s + 3,25)
10	G(s) = 1000/(s2-0,04)

Розрахувати найменшу дестабілізуючу мультиплікативну похибку (НДМП) визначення передавальної функції об’єкту згідно з формулою

НДМП = , .

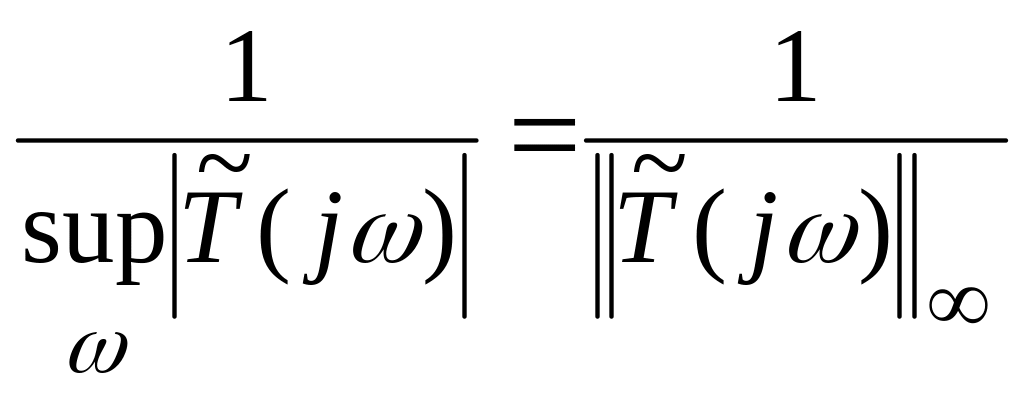3. Зміст звіту

У звіти представити:

1. Варіант завдання.

2. Передавальну функцію об’єкту керування, необхідні розрахунки по алгоритму Евкліду, обгрунжтований вибір параметру Q(s) для забезпечення доброї якості системи керування і передавальну функцію стабілізуючого регулятору K(s).

3. Результати моделювання замкненої системи при одиничному вхідному діянні, перелік команд Matlab або структурну схему в Matlab/Simulink.

4. Привести значення НДМП і її трактування.

5. Аналіз отриманих результатів.

6. Висновки по роботі.

Література

1. Дорф Р. Современные системы управления / Р. Дорф, Р. Бишоп. Пер. с англ. Б.И.Копылова. – М.: Лаборатория базовых знаний, 2002. – 832 с.

2. Зайцев Г.Ф. Теорія автоматичного керування/ Г.Ф. Зайцев, В.К. Стеклов, О.І. Бріцький. За ред. проф. Г.Ф. Зайцева. – К.:Техніка, 2002. – 688 с.

3. Изерман Р. Цифровые системы управления / Р. Изерман. – М.: Мир, 1984. – 541 с.

4. Куо Б. Теория и проектирование цифровых систем управления / Б. Куо. – М.: Машиностроение, 1986. – 448 с.

5. Медведев В.С. Control System Toolbox. MATLAB 5 для студентов / В.С. Медведев, В.Г. Потемкин. – М.: ДИАЛОГ-МИФИ, 1999. – 278 с.

6. Методы классической и современной теории автоматического управления: [учебник в 5-и тт.; 2-е изд., перераб. и доп.] Т.3: Синтез регуляторов систем автоматического управления / Под ред. К.А. Пупкова и Н.Д. Егупова. – М.: Издательство МГТУ им. Н.Э. Баумана, 2004. – 616 с.

7. Рафіков Г.Ш. Сучасна теорія керування дискретних динамічних систем: [навчальний посібник] / Г.Ш. Рафіков. – Донецьк: Норд-пресс, 2005. – 345 с.

8. Ротач В.Я. Теория автоматического управления: [учебник для вузов] / В.Я. Ротач. – 5-e изд., перераб. и доп. – М.: Издательский дом МЭИ, 2008. – 396 с.

9. Стрейц В. Метод пространства состояний в теории линейных дискретных систем управления / В. Стрейц. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 296 с.

10. Филлипс Ч. Системы управления с обратной связью / Ч. Филлипс, Р. Харбор . – М.: Лаборатория базовых знаний, 2001. – 616 с.