2. Завдання

В наведеної нижче таблиці вказані номінальні параметри передавальні функції об’єкту керування, а також адитивна і мультиплікативна невизначеність об’єкту. Адитивна або мультиплікативна невизначеність об’єкту керування представлені передавальними функціями, які є досить доброю апроксимацією вказаних невизначеностей.

Таблиця 1 – Таблиця варіантів

№ варіанту	Передавальна функція обьєкту	Адитивна невизначеність	Мультиплікативна невизначеність
1
2
3
4
5
6
7
8
9
10

Для заданого в відповідному варіанті об’єкту керування необхідно засобами Matlab спроектувати P-, PI-, PID-регулятори, для чого потрібно виконати наступні кроки:

1) за допомогою Matlab/Simulink створити структурну схему замкненої системи, яка показана на рис. 6, і завдати передавальну функцію об’єкту керування .

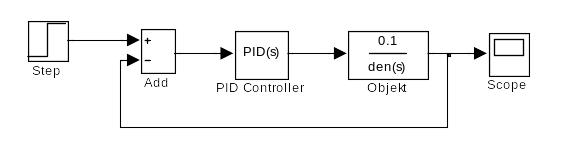
Рисунок 6 – Структурна схема системи для обрання параметрів регулятору

2) подвійним клацанням мишкою по блоку “PID Controller” відкрити вікно для налагодження регулятору. Тут слід обрати PID-регулятор, залишити позначку ”Continuous-time”, Controller Form - “Parallel” , встановити навчальні параметри регулятору (наприклад, P =1, I = 1; D = 0; N = 10), натиснуть кнопку “Apply” і потім натиснуть кнопку “Tune”;

3) в новому вікні буде показано перехідний процес для параметрів регулятору, які показані праворуч, якщо натиснути стрілку “Show parameters”. Перехідний процес можна покращити шляхом переміщення повзунка ліворуч (“Slower”) або праворуч (“Faster”);

4) параметри регулятору, які отримані в результаті виконання пункту с), необхідно експортувати до робочої області Matlab, для чого слід натиснути кнопку уверху з піктогамою ”Export plant or controller to workspace”;

5) в командному вікні Matlab слід виконати команду tf(C), результатом якої буде передавальна функція регулятору.

Пункти від 2) до 5) необхідно повторити для отримання параметрів PI- і P-регуляторів.

Після того, як параметри регуляторів визначені, необхідно провести дослідження стійкості замкненої системи з урахуванням адитивної і мультиплікативної невизначеності моделі об’єкту. Для перевірки робастної стійкості замкненої системи використовуються один або кілька критеріїв стійкості (7) – (10) або (14) – (16).

2.1 Методичний приклад

Нехай номінальною передавальною функцією об’єкту і передавальною функцією регулятору є відповідно, а адитивна невизначеність може бути добре апроксимованою передавальною функцією . У логарифмічному масштабі має наступний вигляд (рис. 7).

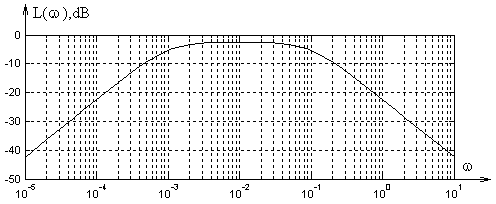
Рисунок 7 – ЛАЧХ адитивної невизначеності передавальної функції об’єкту

При частоті =0 статичний коефіцієнт підсилення об’єкту визначений досить точно, тому . В області високих частот в наслідок того, що об’єкт має властивості фільтру низьких частот, , тому і .

Мультиплікативна похибка визначається як відношення адитивної похибки до номінальної комплексної передавальної функції, тобто . Якщо адитивна похибка встановлена, то легко визначити і мультиплікативну похибку (рис. 8). У даному прикладі можна апроксимувати передавальною функцією виду

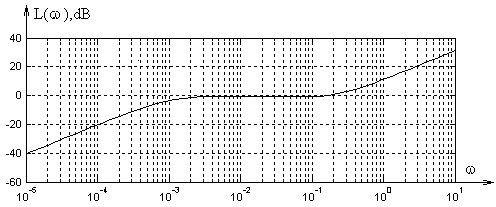
Рисунок 8 – ЛАЧХ мультиплікативної невизначеності

Для оцінки робастної стійкості замкненої системи з врахуванням адитивної невизначеності нехай буде використано критерій (7), для якого потрібні передавальна функція регулятору, функція чутливості и адитивна похибка. За допомогою функції Matlab tf( ) створимо потрібні функції: K=tf([3 1.3 0.11],[1 0.5 0]) – для регулятору, F=tf(1,[37.5 12.5 1]) – для об’єкту, S = feedback(1,K*F,-1) – функція чутливості, Ad=tf([950 0],[1e4 1010 1]) – адитивна похибка. Після чого достатньо побудувати ЛАЧХ продукту K*F*Ad і перевірити, чи буде ЛАЧХ менш ніж нуль. В наведеному прикладі ЛАЧХ у діапазоні 0,1≤ ω ≤0,3 (див. рис.8) більш ніж нуль, тобто модуль продукту |K*F*Ad(jω)| більш одиниці, а це означає, що робастна стійкість системи на гарантується. Аналогично перевіряеться робастна стійкість для системи з мультиплікативною невизначеностю.

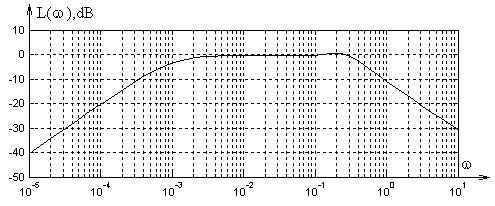
Рисунок 9 – ЛАЧХ послідовного включення регулятору, функції

чутливості і адитивної похибки. Робастна стійкість не гарантована.

3. Зміст звіту

У звіти представити:

1. Варіант завдання.

2. Графічне представлення і апроксимацію передавальними функціями адитивної і мультиплікативної невизначеності передавальної функції об’єкту.

3. Передавальні функції P-, PI-, PID-регуляторів і оцінку робастної стійкості системи з кожним з цих регуляторів як для адитивної, так і для мультиплікативної похибки визначення передавальної функції об’єкту.

4. Аналіз отриманих результатів.

5. Висновки по роботі.