1.2 Синтез модального регулятора для слідкуючої системи
Багатовимірний об’єкт керування з інтегратором описується рівнянням стану
.
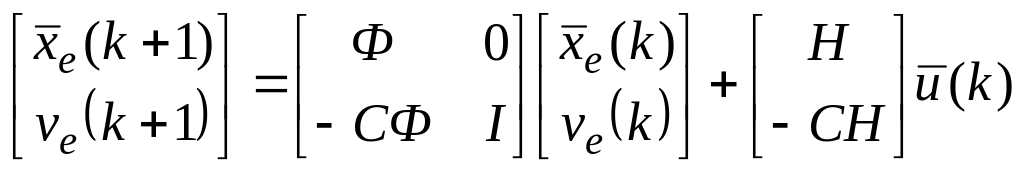(9)
.
Керуючий вплив розраховується за формулою
,
,
(10)
де 
–
матриця зворотного зв'язку модального
регулятора;
– матриця
коефіцієнтів передачі інтегрального
контролера.
Головна
ідея
в
методиці
синтезу
модального
регулятора
слідкуючої
системи
полягає
в
тому,
щоб
він
забезпечував
точне
відстеження
керуючого
впливу,
тобто
щоб
новий
вектор
помилки
звертався
у
нуль
при
будь-якій
початковій
умові
.
Рівняння замкнутої системи
,
(11)
.
(12)
Методика синтезу матриці зворотного зв'язку модального регулятора з інтегральним контролером аналогічна методиці синтезу модального регулятора, розглянутої раніше, але необхідно пам’ятати, що синтез регулятора необхідно проводити для об’єкта керування заданого рівнянням (9).
2. Завдання Задані рівняння стану та рівняння виходу безперервної динамічної системи
,
.
Таблиця 1 – Таблиця варіантів
№ варіанту |
Матриці безперервної системи |
Час перехідного процесу, с |
1 |
A=[1 -2; 4 -1], B=[1 0; 1 2], C=[1 0; 0 1] |
1 |
2 |
A=[3 1; -1 2], B=[0.1 1; 1 -4], C=[0 1; 0.2 1] |
2 |
3 |
A=[-4 9; 1 -3], B=[1 -2; 1 0], C=[0 0.1; 1 1] |
3 |
4 |
A=[0 2; 2 -1], B=[1 0.5; 1 -2], C=[10 0; 0 1] |
4 |
5 |
A=[-2 -9; -1 -2], B=[1 1; -1 -3], C=[4 1; 0 2] |
5 |
6 |
A=[-2 -1; -1 3], B=[-2 1; 1 0], C=[1 0; 2 2] |
6 |
7 |
A=[10 -1; 2 -3], B=[2 1; -1 1], C=[10 0; 0.1 -2] |
7 |
8 |
A=[9 0; -1 -2], B=[2 0; 2 1], C=[2 0; 0.1 -1] |
8 |
9 |
A=[-5 -2,5; 1 8], B=[1 0; -1 -1], C=[1 2; 0.1 1] |
9 |
10 |
A=[-1 -1;-1 2], B=[1 0.1; 2 -5], C=[1 0; -2 1] |
10 |
Згідно таблиці варіантів необхідно:
1) здійснити перехід від безперервної системи до цифрової з періодом дискретності Т (обґрунтувати та обрати величину Т самостійно);
2) провести синтез (обґрунтувати та обрати бажані полюси самостійно):
- модального регулятора;
- модального регулятора з інтегральним контролером.
3) отримати графіки перехідних процесів замкнутої системи по змінним стану, виходу, керуючим впливам та провести аналіз отриманих результатів;
4) провести дослідження робастних властивостей синтезованих регуляторів, для цього необхідно отримати графіки перехідних процесів при відхилені параметрів системи від номінальних значень;
5) побудувати в Simulink структурну схему замкнутої системи з модальним регулятором, модальним регулятором та інтегральним контролером, і отримати графіки перехідних процесів;
6) зробити висновки за результатами дослідження.
3. Зміст звіту
У звіти представити:
1. Варіант завдання.
2. Стислі теоретичні відомості.
3. Лістинг програми моделювання, розрахунки та перехідні процеси.
4. Структурні схеми замкнутої системи в Simulink та графіки перехідних процесів.
5. Аналіз отриманих результатів.
6. Висновки по роботі.