Химические реакторы

Химическим реактором называется аппарат, в котором осуществляются химические процессы, сочетающие химические реакции с массо- и теплопереносом.

Все аппараты, расположенные до реактора, предназначены для подготовки сырья и химической переработки. Всё то, что находится после реактора, необходимо для разделения получающихся в результате реакции продуктов.

Классификация реакторов

При классификации реакторов принимают во внимание следующие основные признаки:

1. Характер операций, протекающих в реакторе

2. Режим движения реакционной среды

3. Тепловой режим

4. Фазовое состояние реагентов

По 1 признаку реакторы делят на периодические, непрерывные и полунепрерывные. Реакторы непрерывные, т. е. с непрерывной подачей реагентов, в свою очередь делят по характеру движения реакционной среды (т. е. по гидродинамической обстановке) на реакторы идеального вытеснения и реакторы идеального смешения.

Структура математической модели химического реактора

Методы расчета и проектирования химических реакторов основаны на моделировании реакторов и процессов в них.

Моделирование – это метод изучения различных объектов, при котором исследование проводят на модели, а результаты количественно распространяют на оригинал. Модель может представлять собой уменьшенную по определенным законам (или в некоторых случаях увеличенную) копию реального объекта. Но моделью может быть и определенная система представлений о реальном объекте, выражаемая как совокупность математических структур, уравнений, неравенств, таблиц, графиков. Такую модель называют математическим описанием объекта или его математической моделью.

Математическая модель химического реактора должна быть с одной стороны достаточно простой, с другой стороны – достаточно точно передавать количественные закономерности протекания процесса. Эти требования находятся в противоречии и разработка математической модели реактора весьма сложная задача.

При разработке математической модели целесообразно использовать иерархический подход к реактору как к сложной системе. (Иерархия – это расположение частей или элементов целого в порядке от высшего к низшему). Суть этого подхода состоит в том, что сложная система рассматривается как совокупность подсистем, связанных между собой.

Реактор и реакционный узел, будучи сложными объектами, имеют многоступенчатую структуру и их математические модели строятся последовательно на основе предварительного построения их составных частей и введения соотношений, связывающих переход с одного уровня на другой. Важную роль математического описания химического реактора играют балансовые уравнения, являющиеся выражением общих законов сохранения массы и энергии.

n_{j вх} – n_{j вых} -n_j X_р = n_{j нах} ,

где n_{j вх} – количество вещества j, внесенное в элементарный объем ΔV за время Δτ с потоком участников реакции.

Q_вх – Q_вых Q_хр Q_т.о. = Q_нач

Q_вх – теплосодержание веществ, входящих в объем ΔV за время Δτ;

Q_хр – теплота, выделившаяся или поглотившаяся в результате химической реакции;

Q_т.о – теплота, израсходованная на теплообмен объема ΔV за время Δτ;

Для составления материального баланса по веществу А будем считать, что объемный расход реакционной смеси на входе в реактор V₀, м³/ч, на выходе V. Концентрация вещества А в потоке, входящем в реактор C_A,0, кмоль/м³, концентрация вещества А в выходящем потоке и в любой точке реактора составляет C_A, кмоль/м³, химическая реакция протекает со скоростью W_A кмоль/м³ ч, определяемый и рассматриваемый промежуток времени dτ, при постоянной температуре, концентрации C_A.

Тогда за время dτ в объем реактора V войдет n_{A вх} = C_A,0 V₀ dτ, выйдет из реактора n_{A вых} = C_A V dτ. Израсходуется на химическую реакцию n_{A х.р.} = W V_р dτ.

Так как в реакторе находится C_AV_р моль вещества А, изменение этого количества за время dτ составит n_{A мак} = d (C_A V_р)

Таким образом уравнение материального баланса по веществу А для реактора идеального смешения имеет вид

C_A,0 V₀ dτ - C_A V dτ – W_A V_р d τ = d (C_A V_р)

Все члены этого уравнения измеряются в единицах количества вещества (кмоль). Разделим левую и правую часть на d τ

C_A,0 V₀ - C_A V - W V_р = (1) - мольные потоки вещества в единицу времени. Правая часть уравнения представляет собой скорость накопления вещества в реакторе. При постоянном объеме V_р скорость накопления можно представить

V_р dC_A / dτ

Рассмотрим отдельный случай. Периодический реактор идеального смешения по условию

V₀ = 0, V = 0.

или

C_A = C_A,0 (1 – X_A)

dC_A = - C_A,0 dX_A

Реактор идеального смешения периодический РИС-П

Реагенты загружаются в начале операции. При этом процесс слагается из трех стадий: загрузки сырья, его обработки (химическое превращение) и выгрузка готового продукта. После проведения всех этих операций они повторяются вновь. Продолжительность одного цикла, проводимого в периодическом реакторе, определяется по уравнению

τ_п = τ + τ_всп ,

где τ_п - полное время цикла;

τ – рабочее время, затрачиваемое на проведение химической реакции;

τ_всп – вспомогательное время

Реактор идеального смешения периодический называемый сокращенно РИС – П, представляет собой аппарат с мешалкой, в который периодически загружаются реагенты. В таком реакторе создается весьма интенсивное перемешивание, поэтому в любой момент времени концентрация реагентов одинакова во всем объеме аппарата и изменяется лишь во времени, по мере протекания химической реакции. Такое перемешивание можно считать идеальным, отсюда и название реактора.

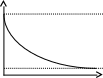
Реактор идеального смешения периодический

С

C_{A, 0} τ = 0

С_А τ = τ

у

Изменение концентрации исходного реагента А во времени и в объеме в РИС – П

Здесь N_A,0 начальное количество исходного реагента А;

X_A,0 – начальная степень превращения реагента А;

C_A,0 – начальная концентрация реагента А в исходной смеси.

N_A, C_A, X_A – то же в конце процесса;

τ – время;

у – пространственная координата (координата места).

Периодические химические процессы по своей природе всегда являются нестационарными (т. е. неустановившимися) , т. к. в ходе химической реакции изменяются параметры процесса во времени (например, концентрация веществ), т. к. происходит накопление продуктов реакции.

Для расчета реактора надо знать его уравнение, позволяющее определить рабочее время τ, необходимое для достижения заданной степени превращения Х_А, при известной начальной концентрации вещества С_А,0 и известной кинетике процесса, т. е. при известной скорости химической реакции W_н .

Основанием для получения уравнения реактора любого типа является материальный баланс, составленный по одному из компонентов реакционной смеси.

В общем случае, когда концентрация компонента непостоянна в различных точках реактора или непостоянна во времени, материальный баланс составляют в дифференциальной форме для элементарного объема реактора. При этом исходят из уравнения конвективного массообмена, в которое вводят дополнительный член W_А , учитывающий протекание химической реакции.

,

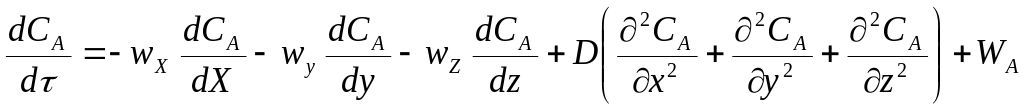где С_А – концентрация реагента в реакционной смеси;

x, y, z – пространственные координаты;

D – коэффициент молекулярной и конвективной диффузии;

W_A – скорость химической реакции.

Исходя из того, что в РИС – П вследствие интенсивного перемешивания все параметры одинаковы во всем объеме реактора в любой момент времени. В этом случае производная любого порядка от концентрации по осям x, y, z равны 0, тогда

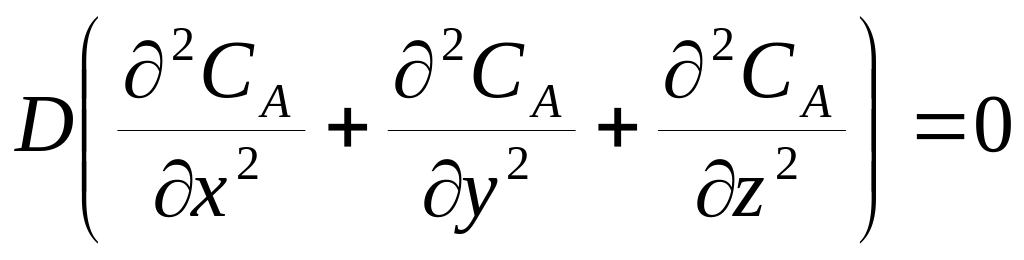
Поэтому уравнение можно записать

Если реакция протекает без изменения объема, то текущая концентрация исходного вещества будет выражаться

С_А = С_А,0 (1 – Х_А)

или

,

где знак “-” указывает на убыль вещества А.

Интегрируя это выражение в пределах изменения времени от 0 до τ и степени превращения от 0 до Х получим уравнение РИС – П

Уравнение является математическим описанием РИС – П. Исходя из этого уравнения можно определить размеры реактора, а также исследовать эту модель с точки зрения нахождения оптимальных значений всех входящих в него параметров.

Реакторы периодического действия просты по конструкции, требуют небольшого вспомогательного оборудования. Поэтому они удобны для проведения опытных работ, изучения химической кинетики. В промышленности они обычно используются в малотоннажных производствах, для переработки дорогостоящих продуктов

.