Занятие 9 Простейшие показательные уравнения и неравенства
1. Некоторые сведения о свойствах и графиках показательной и логарифмической функций
І. Показательная функция.
О.
1.1.
Функция,
заданная формулой
,
(где
,
),
называется
показательной
функцией с основанием а.
Основные свойства показательной функции:
1.
Область определения – множество R
действительных чисел:
R.
2.
Область значений – множество всех
положительных действительных чисел:
.
3.
При
показательная функция возрастает на
множестве
R;
при
показательная функция убывает на
множестве R.
График
функции
(см. рис. 1)
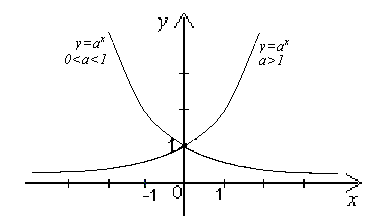
Рисунок 1
Іі. Логарифмическая функция.
О. 1.2. Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число b.
Формулу
(где
,
и
)
называют основным
логарифмическим тождеством.
Свойства логарифмов:
При
любом
и
любых положительных x
и y
справедливы равенства:
1.
2.
3.
4.
5.
для любого действительного
p.
Основные
свойства логарифмов широко применяются
в ходе преобразования выражений,
содержащих логарифмы. Также часто
используется формула
перехода от одного основания логарифма
к другому:
О.
1.3.
Пусть
и
.
Функцию, заданную формулой
называют логарифмической функцией с основанием a.
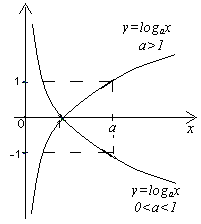
Рисунок 2
Основные свойства логарифмической функции:
1.
2.
R.
3.
Логарифмическая функция на всей области
определения возрастает при
и убывает при
.
График
функции
(см.рис. 2).
2. Решение показательных уравнений
Рассмотрим основные типы показательных уравнений, к ним сводятся все остальные виды показательных уравнений.
І.
Уравнения
вида
,
, 
По
определению логарифма получаем, что
(1).
Если
− алгебраическая функция, то уравнение
(1) будет алгебраическим и его можно
решить с помощью стандартных методов
(так как
−
это некоторое число).
ІІ.
Уравнения
вида
В силу свойств монотонности показательной функции это уравнение равносильно уравнению f (x) = g (x).
ІІІ.
Уравнения
вида
,
Такие уравнения решаются в два этапа:
a)
С помощью замены
это уравнение сводится к уравнению
у которого нужно отобрать все его
положительные
корни
(пусть таких корней ровно n
-
штук).
б)
Решается совокупность уравнений:
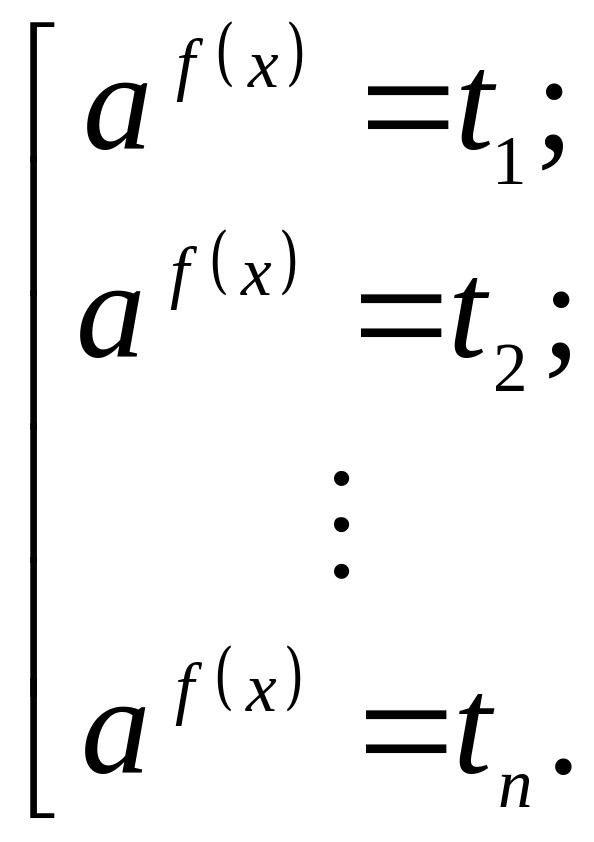
Пример
1.
Решите
уравнение
Δ С помощью правил действия со степенями данное уравнение нетрудно привести к уравнению вида І.
Ответ:
Пример
2.
Решите
уравнение
Δ
Ответ:
Пример
3.
Решите
уравнение
Δ
Так
как
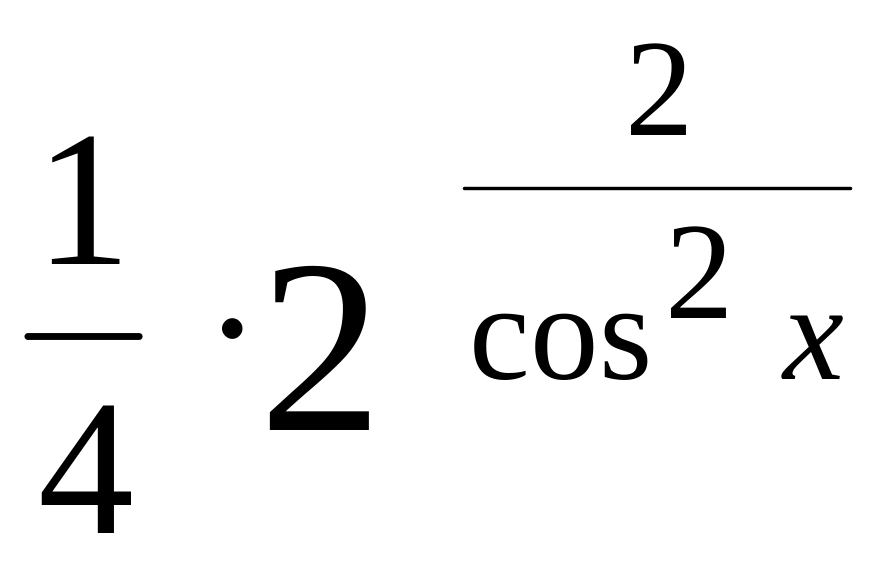
то,
делая замену
получаем
квадратное уравнение
Поскольку
(по свойству показательной функции),
то
– посторонний корень и, следовательно,
исходное уравнение равносильно
уравнению:
Ответ:
