Занятие 7 Основные понятия тригонометрии

1. Градусная и радианная мера угла. Тригонометрическая окружность.

Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. Рассмотрим центральный угол α, у которого одна сторона идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс.

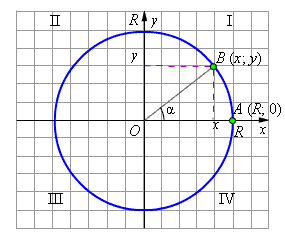
Рисунок 1

O. 1.1. 1. Углом в называется центральный угол, опирающийся на дугу окружности, имеющей длину, равную её части.

Исторически сложилось деление градуса на 60 минут, а минуты на 60 секунд, то есть: , .

Из геометрии известно, что отношение длины дуги l окружности, на которую опирается центральный угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: .

Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан.

O. 1.2. Углом в 1 радиан называется центральный угол, опирающийся на дугу окружности, имеющую длину, равную её радиусу.

Из сказанного выше следует, что полной окружности будет соответствовать в градусах угол . Так как длина всей окружности радиуса R равна 2πR, то всей окружности соответствует угол в радианах, который равен радиан.

Значит, можно написать следующие формулы перехода от градусного измерения к радианному: (1)

и от радианного измерения к градусному: (2)

Из (2) следует, что 1 рад = ,

а из (1) следует, что рад 0,01745 рад.

Обозначение «рад» при записи часто опускают. Например, вместо записи пишут просто .

Пользуясь формулами (1) и (2), легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.

Таблица 1

Угол, градусы
Угол, радианы

Пример 1 Определите радианную меру угла, если его градусная мера равна: 1) 3°; 2) 255°.

Δ Пользуясь формулой (1) получаем:

1) , 2)

_{Ответ: ,}

Пример 2 Перевести радианную меру угла в градусную: 1) 2)

Δ Пользуясь формулой (2) получаем:

1) 2)

Поскольку величина угла в градусной и радианной мере никак не связана с радиусом окружности, то можно рассматривать окружность любого радиуса, проще всего – единичного (R=1) с центром O в начале координат (см. рис. 1). Такая окружность называется тригонометрической окружностью.

Координатные оси делят окружность на четыре дуги, которые называют четвертями. Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора против часовой стрелки. При таком повороте точка A(1;0) перейдёт в некоторую точку B(x;y) на тригонометрической окружности, при этом .

_{Замечание Произвольной точке В(х; у) тригонометрической окружности соответствует не единственный угол α. Таких углов существует бесконечное множество. Они имеют вид α+2πn, где .}

Введём несколько основных определений элементарных тригонометрических функций произвольного угла.

O. 1.3. Косинусом угла α называется абсцисса x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.

O. 1.4. Синусом угла α называется ордината y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.

Из этих определений следует, что и определены для любого и справедлива формула (по теореме Пифагора для ΔАОВ)

O. 1.5. Тангенсом угла α называется отношение ординаты y к абсциссе x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.

O. 1.6. Котангенсом угла α называется отношение абсциссы x к ординате y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.

Из определений 1.5. и 1.6. следует, что для любых допустимых значений _.