2. Основные сведения об элементах электрической цепи.

1. Резистивный элемент (резистор)

В простейшем случае проводника длиной и сечением S его сопротивление определяется выражением (5)

Основной характеристикой резистивного элемента является зависимость (или ), называемая вольт-амперной характеристикой (ВАХ).

Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), характеризуется несколькими параметрами. В частности безынерционному резистору ставятся в соответствие статическое и дифференциальное сопротивления.

2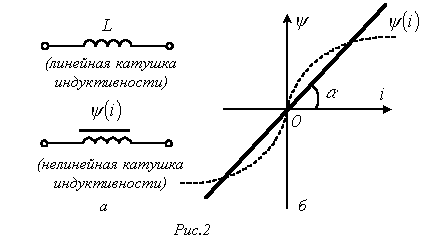 . Индуктивный элемент (катушка индуктивности)

Условное графическое изображение катушки индуктивности приведено на рис. 2,а.

Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,

. (7)

3. Емкостный элемент (конденсатор)

Условное графическое изображение конденсатора приведено на рис. 3,а.

К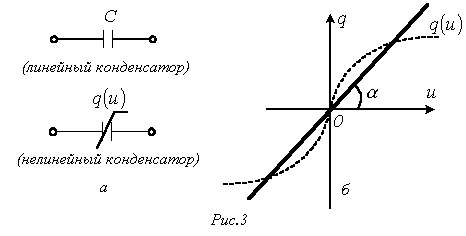 онденсатор – это пассивный элемент, характеризующийся емкостью.

(8)

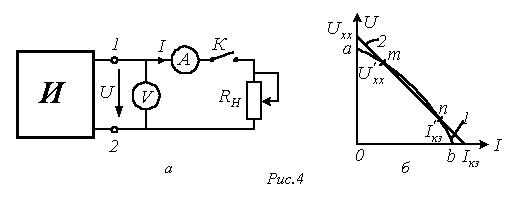
Схемы замещения источников электрической энергии

, (9)

где - напряжение на зажимах источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а); - внутреннее сопротивление источника.

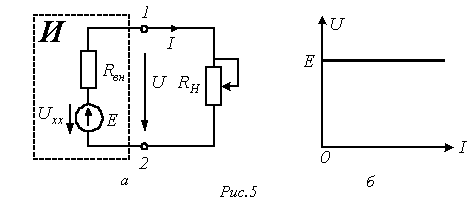
Существует также параллельная схема замещения источника. Для ее описания разделим левую и правую части соотношения (9) на .

В результате получим

или

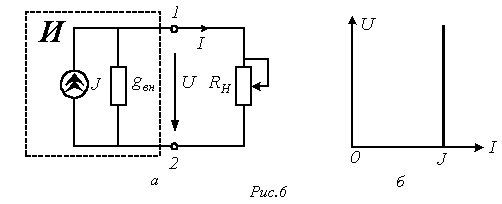, (10) где ; - внутренняя проводимость источника.

Уравнению (10) соответствует схема замещения источника на рис. 6,а.

3. Баланс мощности: (3)

Алгебраическая сумма мощностей вырабатываемых источниками в электрической цепи равна сумме мощностей потребителей включеных в эту цепь. Если положительные направления тока в источнике и направления ЭДС(для источников тока- направления тока источника тока и напряжения) совпадают то произведение запишется со знаком плюс «+», если наоборот, то со знаком минус «-»

Методы расчета электрических цепей постоянного тока

Метод контурных токов(МКТ)

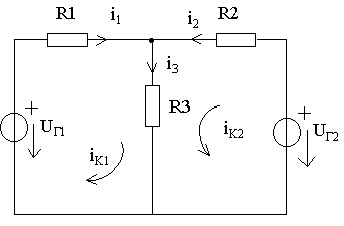
При определении токов и напряжений в отдельных ветвях цепи с n_в-ветвями по законам Кирхгофа в общем случае необходимо решить систему из n_в уравнений.. Метод контурных токов позволяет снизить число решаемых уравнений до числа независимых контуров. В его основе лежит введение в каждый контур условного контурного тока i_к, направление которого обычно выбирают совпадающим с направлением обхода контура. Рассмотрим резистивную цепь, схема которой изображена на рис.6.

Для контурных токов i_к1 и i_к2 этой схемы можно записать уравнения по ЗНК в виде:

-u_г1 + (R₁ + R₃)i_к1 + R₃i_к2 = 0 ; (10)

-u_г2 + R₃i_к1 + (R₂ + R₃)i_к2 = 0. (11)

Перенесем u_г1 и u_г2 в правую часть системы и получим так называемую каноническую форму записи уравнений по методу контурных токов:

R₁₁i_к1 + R₁₂i_к2 = u_к1 , (12)

Рис.6 - Иллюстрация метода контурных токов

R₂₁i_к1 + R₂₂i_к2 = u_к2 , (13)

где R₁₁ = R₁ +R₃; R₂₂ = R₂ + R₃ называют собственными или контурными сопротивлениями 1-го и 2-го контуров; R₁₂ = R₂₁ = R₃ - взаимным сопротивлением 1-го и 2-го контуров;

u_к1 = u_г1; u_к2 = u_г2 - контурными задающими напряжениями. Истинные токи в ветвях находятся как алгебраическая сумма контурных токов: i₁ = i_к1, i₂ = i_к2, i₃ = = i_к1 + i_к2.

Решая систему уравнений, находят величины контурных токов:

i_к1 = Δ₁/ Δ _R ; i_к2 = Δ ₂/ Δ _R ; i_кk = Δ _k/ Δ _R . (14)

где Δ _R - определитель системы:

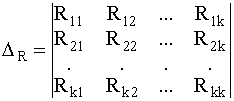. (15)

Определитель _k находится путем замены k-го столбца правой частью приведённой выше системы. Например, для ₁ имеем:

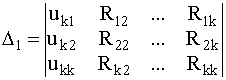. (16)

Полученный результат отражает рассмотренный ранее принцип наложения. Для линейных электрических цепей важную роль играет принцип взаимности (теорема обратимости). Он гласит: если источник напряжения, помещенный в какую-либо ветвь l пассивной линейной электрической цепи, вызывает в другой ветви k ток определенной величины, то этот же источник, будучи помещенный в ветвь k, вызывает в ветви l ток той же величины. Справедливость этого принципа следует непосредственно из уравнений i_kk с учетом того, что _lk = _kl.

Метод двух узлов(метод узлового напряжения)

Этот метод является частным случаем метода узловых потенциалов и применяется для расчета цепей с двумя узлами. Сначала находится узловое напряжение - напряжение между двумя узлами, затем используя закон Ома для участка цепи находят токи в ветвях.

Узловое напряжение находится по следующей формуле:

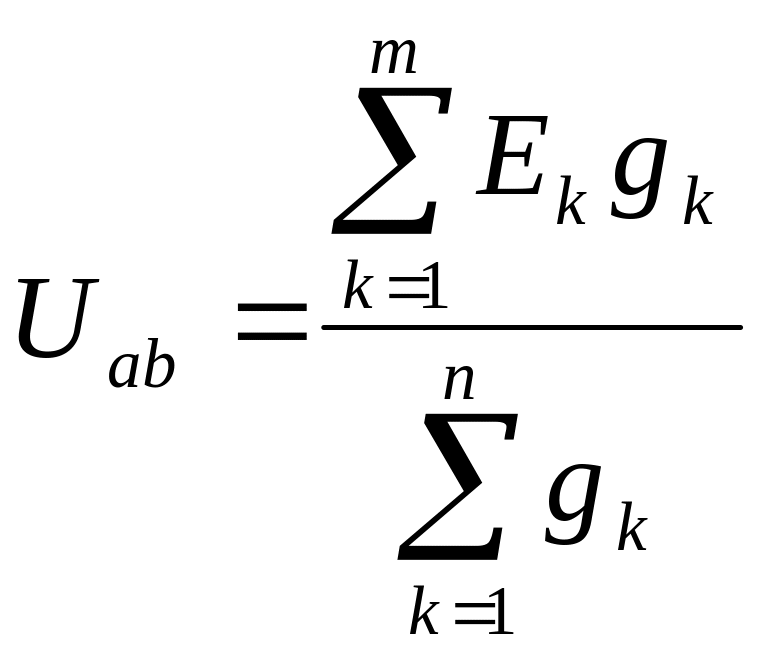(4)

где, - проводимость k-той ветви

- ЭДС k-той ветви

В числителе формулы, в сумму произведение записывается с положительным знаком. Если ЭДС данной ветви направлена к узлу, стоящей первой в индексе узлового напряжения и наоборот, если направлена от узла стоящей первой в индексе узлового напряжения. Это метод является частным случаем МУП. Применяется для схем с двумя узлами. Заключается в нахождении узлового напряжения и применения закона Ома для нахождения токов в ветвях.