3 Лекционный комплекс

Лекция № 1.

Тема: Линейные электрические цепи

Содержание лекции: Введение.Электрические цепи постоянного тока. Основные сведения об элементах электрической цепи. Электрические цепи постоянного тока. Электрические цепи синусоидального тока. Электрические цепи трехфазного тока.

Цель лекции: Ознакомить студентов с задачами изучения дисциплины. Выяснить уровень знаний по разделу «Электричество и электромагнетизм» курса физики. Дать основные сведения об электрических цепях

Ключевые слова: сила тока, напряжение, потенциал, сопротивление, узел, ветвь, контур, звезда, треугольни

Основные параметры цепей.

Электрический ток протекает только в замкнутой цепи под действием ЭДС источника энергии. Как при замкнутой, так и при разомкнутой электрической цепи ЭДС непрерывно поддерживает разность потенциалов между зажимами источника энергии. Потенциал , как известно, это величина, определяющая запас энергии (потенциальную энергию) единицы количества электричества, находящейся в данной точке цепи. Его можно определить по величине работы, которую надо затратить, чтобы переместить одиночный заряд из бесконечности в данную точку цепи. При холостом ходе, т.е. при отсутствии тока в цепи, ЭДС равна разности потенциалов (напряжения) между зажимами источника энергии. Так же как и потенциал, ЭДС измеряется в вольтах.

Н а схемах при изображении источника электрической энергии (элемент E) направление действия ЭДС указываются стрелкой.

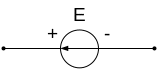
ЭДС всегда направлена от зажима с меньшим потенциалом, который обозначается знаком “-” к зажиму с большим потенциалом, который обозначается знаком “+”.

Ток во внешней по отношению к источнику энергии части цепи протекает от точки с большим потенциалом к точке с меньшим потенциалом. Направление тока на схеме показывается стрелкой.

Величина тока I, протекающего по проводнику, определяется количеством электрических зарядов, проходящих через поперечное сечение проводника в единицу времени.

где q - количество электричества прошедшего за t сек.

Величина, характеризующая противодействие электрической цепи прохождению тока, называется электрическим сопротивлением (R).

Прохождение электрического тока на рассматриваемом участке обусловлено наличием разности потенциалов на его концах, или напряжением U₁₂ =0 на этом участке.

Направление напряжения принимается от точки “1” (с более высоким потенциалом) к точке “2”, где потенциал ниже, т.е. оно совпадает с направлением тока на рассматриваемом участке цепи.

Зависимость напряжения на зажимах какого-либо элемента электрической цепи от тока, протекающего через этот элемент U=f[I] носит название вольт - амперной характеристики.

П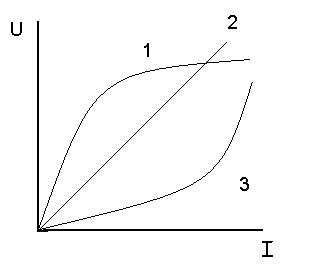 римеры вольт - амперных характеристик

1 – термосопротивление, 2 – резистор, 3 – лампа с металлической нитью.

Как видно из рисунка связь между напряжением и током термосопротивления, лампы с металлической нитью не является линейной. Резистор имеет линейную вольтамперную характеристику.

Элементы с нелинейными характеристиками, называются нелинейными, а элементы с линейными характеристиками называются линейными.

Электрические цепи, состоящие только из элементов с линейными вольтамперными характеристиками, носят название линейных. Большое число реальных электрических цепей можно отнести к линейным. Электрическая цепь, содержащая хотя бы один нелинейный элемент, называется нелинейной.

Электрическая цепь считается разветвленной, если она имеет несколько ветвей, узлов, контуров.

Ветвь - это несколько последовательно соединенных элементов электрической цепи, по которым проходит один и тот же ток. Узел - место соединения трех или более ветвей. Контур - ряд ветвей, образующих электрическую цепь, или замкнутый участок электрической цепи.

В теории электрических цепей различают активные и пассивные участки цепи. Активные участки содержат источники электрической энергии, пассивные - их не имеют.

Закон Ома a) Рассмотрим элементарный пассивный участок цепи.

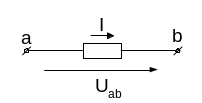
I= = , откуда производные формулы: U=R∙I и R= . “U” называют падением напряжения или напряжением. U_ab=R∙I.

б) Замкнутый контур (неразветвленная цепь).

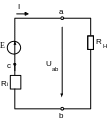
В замкнутом электрическом контуре закон Ома устанавливает связь между ЭДС, сопротивлением и величиной тока. В соответствии с этим законом величина тока прямо пропорциональна электродвижущей силе источника и обратно пропорциональна сопротивлению цепи.

R_H - сопротивление нагрузки, R_i - внутреннее сопротивление источника, U_ab - напряжение на зажимах источника или нагрузки.

I =

в) Активный участок цепи с произвольным числом источников и сопротивлений и заданной разностью потенциалов на концах этого участка имеет вид:

I

a R₁ E₁ R₂ E₂ R₃ b

U_ab= _a- _b

Пусть ток I на участке схемы направлен от “a” к “b”.

Выбранное направление условились называть положительным.

Если принять за направление тока I на участке “a - b” направление от точки “a” к точке “b”, то _a > _b и U_ab = _a - _b совпадает с направлением тока.

Отсюда закон Ома для активного участка цепи будет иметь вид: I=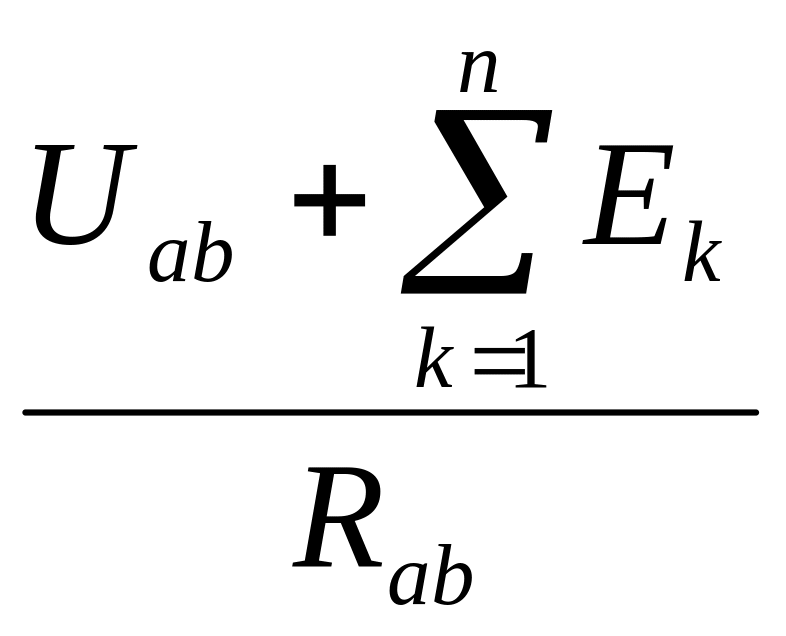 ; где R_ab - суммарное сопротивление участка схемы; - алгебраическая сумма ЭДС источников энергии, имеющихся на данном участке схемы.

ЭДС, совпадающая по направлению с током, записывается с положительным знаком, а не совпадающая - с отрицательным.

Если в результате расчёта получится отрицательная величина, то это означает, что действительное направление тока не совпадает с выбранным направлением, принятым за положительное и необходимо изменить направление тока на обратное.

Законы Кирхгофа являются основополагающими законами электротехники. Они полностью определяют электрическое состояние цепей и лежат в основе всех электротехнических расчетов.

Первый закон Кирхгофа Первый закон Кирхгофа применяется к узлам электрической схемы и формулируется следующим образом: алгебраическая сумма токов ветвей сходящихся в любом узле равна нулю Здесь l - это число ветвей, сходящихся в рассматриваемом узле.

Токи ветвей берутся со знаком плюс, если ток направлен к узлу, и со знаком минус, если ток направлен от узла. Можно принять и наоборот.

Для примера рассмотрим только один “А” любой сложной электрической схемы.

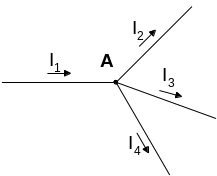
Выберем произвольно направления токов ветвей. Уравнение по первому закону Кирхгофа выглядит следующим образом: I₁ – I₂ – I₃ – I₄ = 0

Первый закон Кирхгофа является интерпретацией того факта, что в узлах заряды не могут накапливаться или возникать, так как это привело бы к изменениям потенциалов узлов и токораспределению в ветвях.

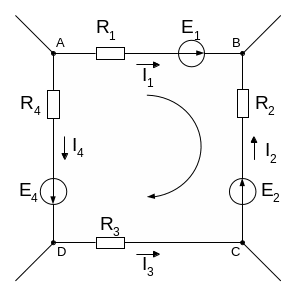
Второй закон Кирхгофа Этот закон применяется к контурам электрической цепи и формулируется следующим образом: алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений на отдельных участках того же контура.

Математическая запись второго закона Кирхгофа имеет вид:

Здесь m - число источников ЭДС, входящих в данный контур, n - число участков, образующих его. При этом со знаком плюс берутся ЭДС и токи, направления которых совпадают с произвольно выбранным направлением обхода данного контура, и со знаком минус, если их направления не совпадают с направлением обхода.

Рассмотрим один участок сложной цепи. Составим уравнение для контура ABCDA, производя обход контура по часовой стрелке. Выберем условно-положительное направление токов ветвей, входящих в рассматриваемый контур ABCDA. Согласно сказанному выше относительно правила знаков, составим следующее уравнение: E1 – E2 – E4 = R1I1 – R2I2 – R3I3 – R4I4

Правила составления уравнений:

1. Выбираем направления токов в ветвях произвольно

2. Для уравнений по первому закону токи входящие в узел записываем с одним знаком, а выходящие- с обратным знаком

3. Направление обхода контуров выбираем один для всех рассматриваемых контуров

4. Общее число уравнений по двум законам Кирхгофа равно числу неизвестных токов или числу ветвей.

5. Число уравнений по первому закону Кирхгофа равно число узлов минус один (У-1)

6. Оставшиеся уравнения записываются по второму закону.

Метод эквивалентных преобразований (упрощения схемы)

Сущность этого метода состоит в том, что какая-либо электрическая цепь путем замены ряда последовательно и параллельно соединенных элементов на эквивалентные, в смысле идентичности режима работы электрической цепи в целом, преобразуется к простейшей схеме вида

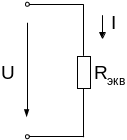
Данная схема рассчитывается на основании закона Ома I = , где R_экв – эквивалентное сопротивление схемы.

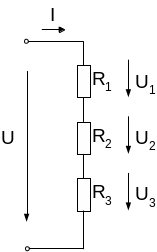
Последовательное соединение:

На основании II закона Кирхгофа U = U1 + U2 + U3 или U= R1I+ R2I+ R3I = (R1+ R2+ R3)I = RэквI I= ; Rэкв = R1 + R2 + R3

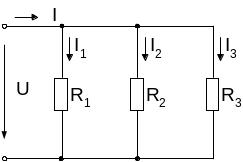
Параллельное соединение:

На основании I закона Кирхгофа: I = I1 + I2 + I3 = U = или эквивалентная проводимость схемы равна gэкв = g1 + g2 + g3, где gэкв=1/ Rэкв, g2=1/ R2, g3=1/ R3

В частном случае, при параллельном соединении двух резисторов R₁ и R₂ R_экв =

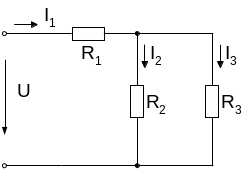
При смешанном соединении резисторов определение эквивалентного сопротивления цепи производится поэтапно.

Например, пусть дана схема со смешанным соединением R1, R2, R3 резисторов. Сначала определяется сопротивление параллельно включенных резисторов R2 и R3 R23 =

Затем находится эквивалентное сопротивление последовательно соединенных резисторов R₁ и R₂₃

R_экв = R₁ + R₂₃ = R₁ +

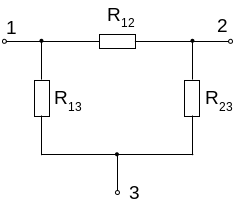
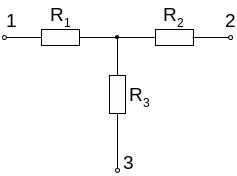
Преобразование элементов, соединенных по схемам звезды и треугольника

В ряде случаев встречаются соединения групп элементов, для которых необходимо выполнить преобразования элементов, соединенных по схемам трехлучевой звезды или по схеме треугольника. После этого можно выполнить эквивалентные преобразования и определить входное сопротивление цепи.

Преобразования треугольника в звезду.

осуществляется с помощью следующих формул:

R₁ = ,R₂ = ,R₃ = .

Формулы обратного преобразования звезды в треугольник имеют вид:

R₁₂=R₁+ R₂+ ,R₁₃=R₁+ R₃+ ,R₂₃=R₂+ R₃+ .