1. Крамер формуласы арқылы теңдеу жүйесін шешу

2. Кері матрица арқылы теңдеу жүйесін шешу.

3. Матрицалардың амалдарын орындау.

4. Теңдеудің шешім табу.

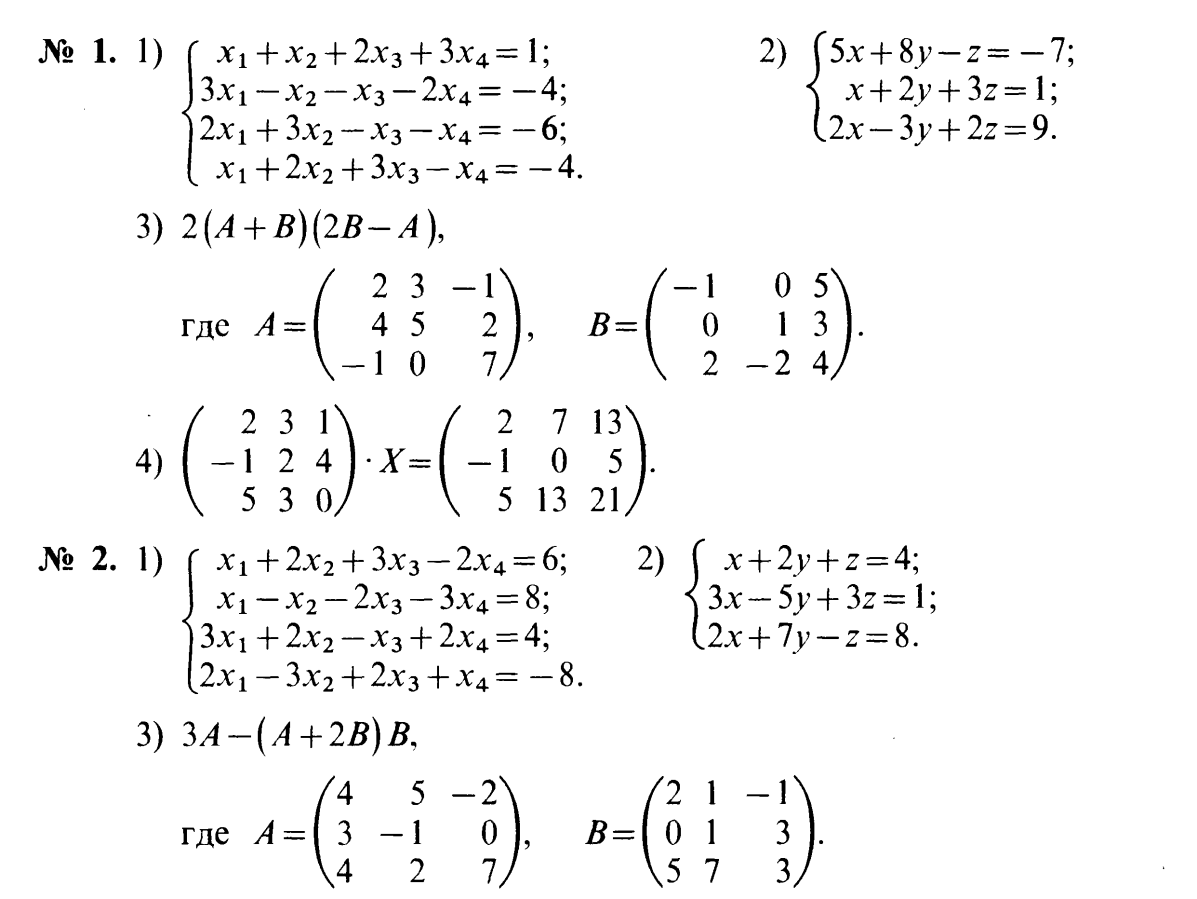
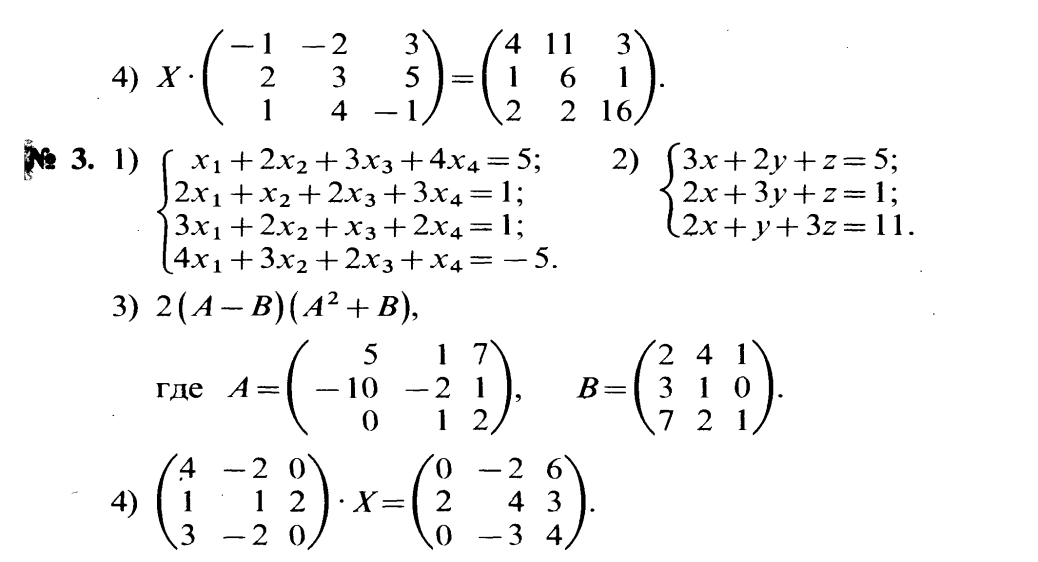
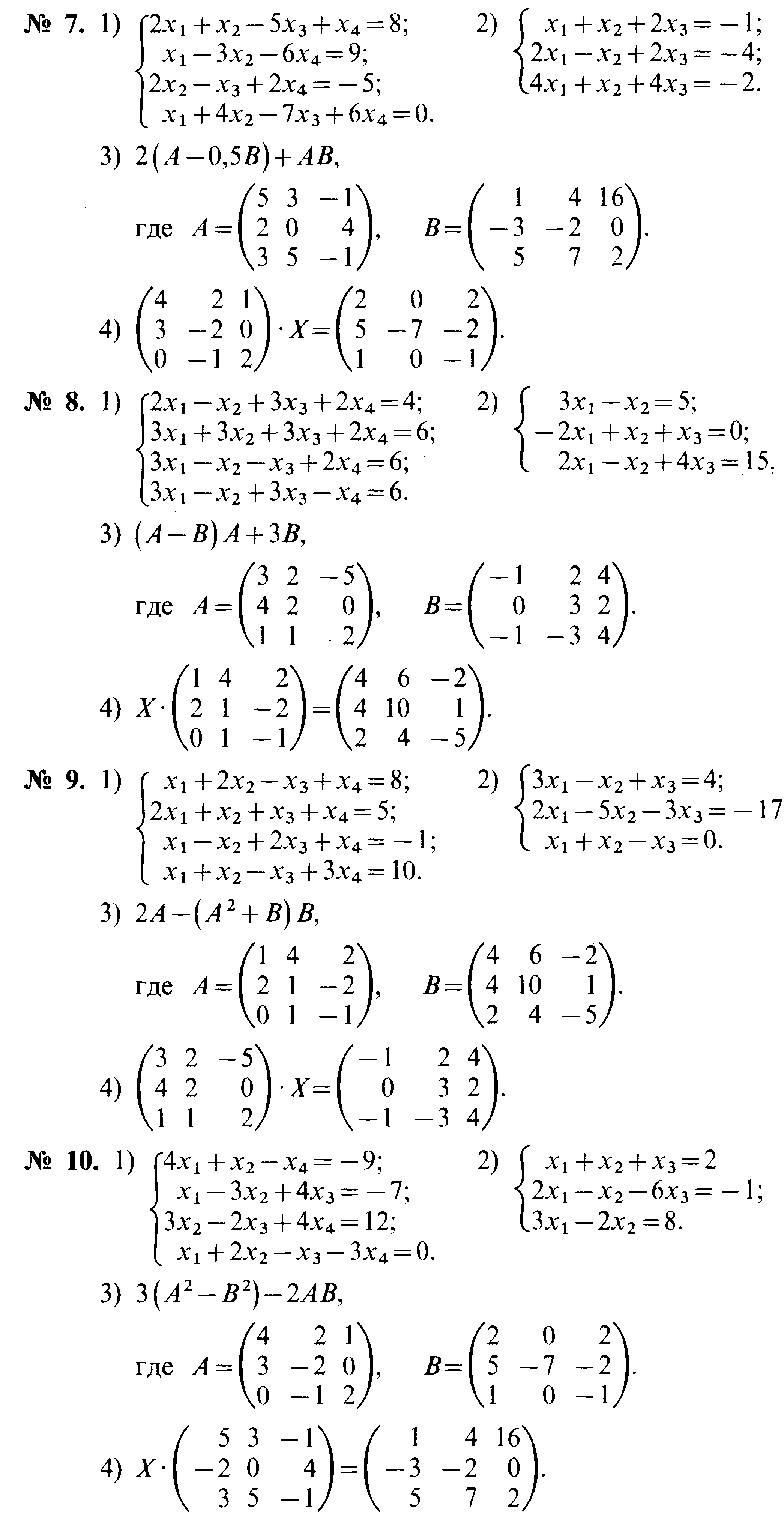
Тәжірибелік жұмыс №2

1. Гаусс әдіс пайдаланып сызықтық теңдеу жүйесін шешу.

Процедура біртекті емес n белгісізі бар n сызықты алгебралық теңдеулер жүйесін шығарады

a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1

. . . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Бастапқыда нольден айрықша x₁ коэффициентті анықтаймыз. Сәйкес келетін теңдеуді біріншісімен алмастырамыз (егер керек болса). нольден айрықша a₁₁ жүйесін аламыз. Осы теңдеудің барлық коэффиценттерін a₁₁ бөліп, келесіні аламыз:

x₁+b₁₂ x₂+ . . .+b_1n x_n=b_1n+1

Осы теңдеу көмегімен берліген теңдеуден x₁ алып тастаймыз.

a⁽¹⁾₂₂ x₂+a⁽¹⁾₂₃ x₃+ . . .+a⁽¹⁾_2n x_n=a⁽¹⁾_2n+1

. . . .

a⁽¹⁾_n2 x₂+a⁽¹⁾_n3 x₃+ . . .+a⁽¹⁾_nn x_n=a⁽¹⁾_nn+1

мұнда

a⁽¹⁾_{i j}=a_{i j}-a_{i 1}b_{1 j}, i,j= 2...n

Алынған жүйе n-1 теңдеуден тұрады. Сипатталған процедураны осы жүйеге қолданамыз. Операцияны керекті сан ретінде қайталаймыз, жүйені үшбұрышты түрге келтіргенше.

x₁+с₁₂ x₂+ . . .+с_1n x_n=с_1n+1

x₂+ . . .+c_2n x_n=c_2n+1

. . . .

x_n=c_nn+1

Енді x_n,x_n-1, . . ., x₁. анықтау жеңіл.

Мысалы:

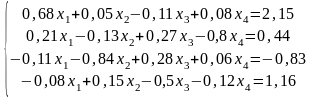
Шешу жолы:

Гаусс әдіс пайдаланып сызықтық теңдеу жүйесін MS Excel арқылы шешу болады.

Түзу жолы
теңделер	х1	х2		х3		х4		бос мүшесі
I	0,68	0,05		-0,11		0,08		2,15
II	0,21	-0,13		0,27		-0,8		0,44
III	-0,11	-0,84		0,28		0,06		-0,83
IV	-0,08	0,15		-0,5		-0,12		1,16
1 қадам
барлық теңдеулердің х1 коэффициенттерін бірлікке келтірледі
теңделер	х1	х2		х3		х4		бос мүшесі
I	1	0,073529		-0,16176		0,117647		3,161764706
II	1	-0,61905		1,285714		-3,80952		2,095238095
III	1	7,636364		-2,54545		-0,54545		7,545454545
IV	1	-1,875		6,25		1,5		-14,5
2 қадам
2,3,4 теңдеулердің х1 айнымалылары жойылады
теңделер	х1	х2		х3		х4		бос мүшесі
I	1	0,073529		-0,16176		0,117647		3,161764706
II	0	0,692577		-1,44748		3,927171		1,066526611
III	0	-7,56283		2,38369		0,663102		-4,38368984
IV	0	1,948529		-6,41176		-1,38235		17,66176471
3 қадам
2,3,4 теңдеулердің х2 коэффициенттерін бірлікке келтірледі
теңделер	х1	х2		х3		х4		бос мүшесі
I	1	0,073529		-0,16176		0,117647		3,161764706
II	0	1		-2,08999		5,670374		1,539939333
III	0	1		-0,31518		-0,08768		0,579635849
IV	0	1		-3,29057		-0,70943		9,064150943
4 қадам
3,4 теңдеулердің х2 айнымалысы жойылады
теңделер	х1	х2		х3		х4		бос мүшесі
I	1	0,073529		-0,16176		0,117647		3,161764706
II	0	1		-2,08999		5,670374		1,539939333
III	0	0		-1,77481		5,758053		0,960303483
IV	0	0		1,200576		6,379808		-7,52421161
5 қадам
3,4 теңдеулердің х3 коэффициенттерін бірлікке келтірледі
теңделер	х1	х2		х3		х4		бос мүшесі
I	1	0,073529		-0,16176		0,117647		3,161764706
II	0	1		-2,08999		5,670374		1,539939333
III	0	0		1		-3,24433		-0,54107544
IV	0	0		1		5,313955		-6,26716732
6 қадам
4 теңдеуден х3 коэффициенті жойылады
теңделер	х1	х2		х3		х4		бос мүшесі
I	1	0,073529		-0,16176		0,117647		3,161764706
II	0	1		-2,08999		5,670374		1,539939333
III	0	0		1		-3,24433		-0,54107544
IV	0	0		0		-8,55829		5,726091884
Кері жолы
біртіндеп айнымалыларды табылады
х4 =	5,726092	=		-0,66907
	-8,55829
x3 = -0,541075 + 3,24433x4
x3 = -2,711
x2=1,5399-5,6703x3+2,0899x2
x2 = -0,334
x1 = 3,1617 - 0,1176x4 + 0,1617x3 - 0,0735x2
x1 = 2,826

Жауабы: 2,826; -0,334; -2,711; -0,669

Тапсырмалар:

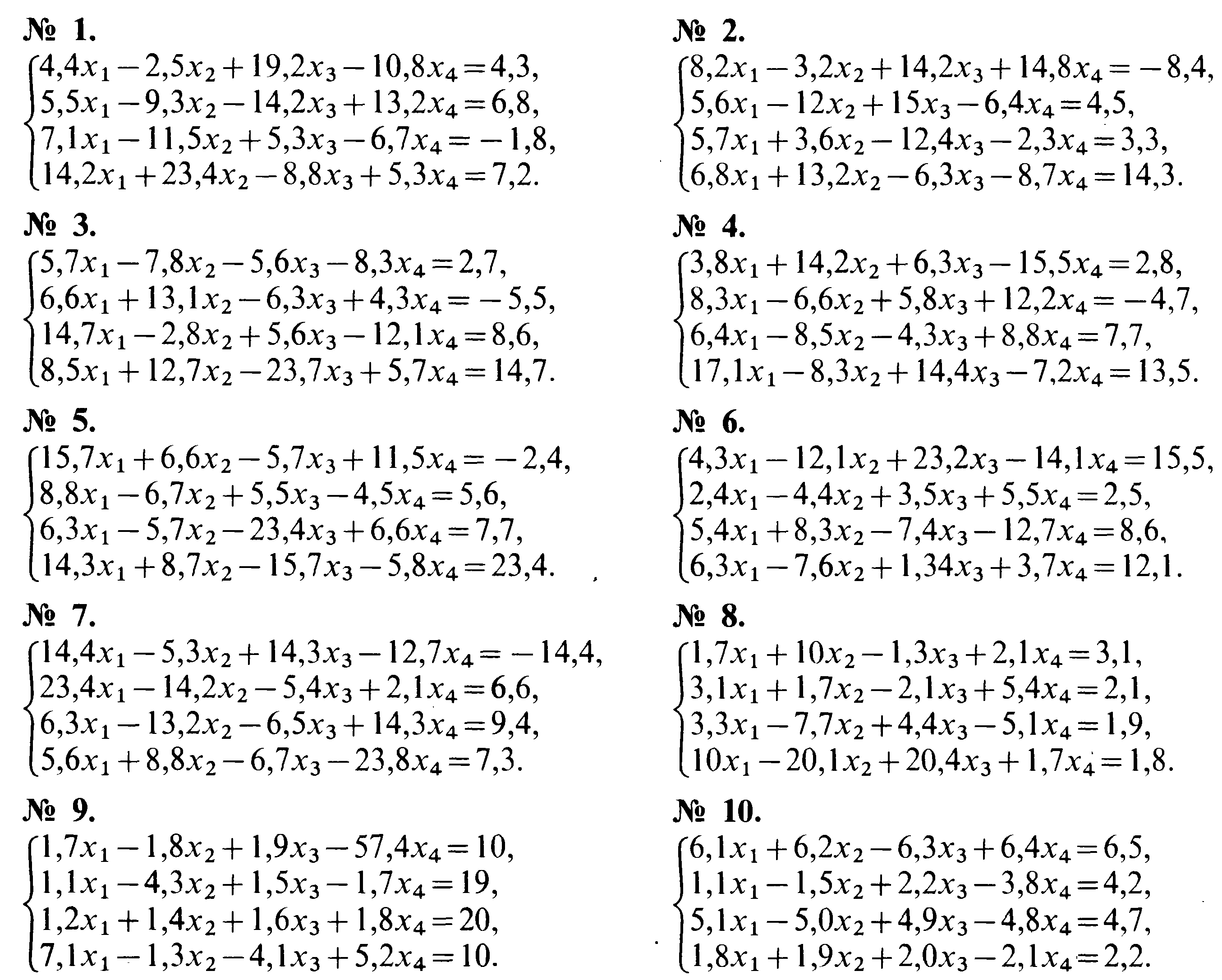
1. Итерация әдісін пайдаланып сызықтық теңдеуді шешу. ( ε =0,001)

Бұл әдісті қолдану үшін бастапқы теңдеу жүйесін келесі түрде жазылады.

X=f(x)

Түбірдің бастапқы жуық шамасы х=c₀ белгісін, оны алдағы теңдеудің оң бөлігіне қойсақ

С1=f(c0)

Түбірдің жаңа мәнін х=f(x) қоямыз, сонда С_n+1=f(C_n), n=1,2; егер екі тізбектелген итерация қорытындысы жақын болса: ⌡С_n+1-C_n⌡ < ε , онда итерациялық процесс тоқталады. Қарапайым итерациялық әдістің негізгі шартына │f(C_n)│<1 сәйкес келсе жеткілікті.

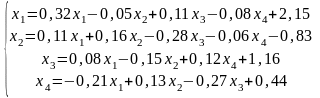
Шешу жолы:

1 итерация:

х1 = х2 = х3 = х4 = 0 болған жағдайда теңдеу жүйесінің шешімі бос мүшелеріне тең болады.

2 итерация:

Берілген теіңдеулерге 1 итерациядағы шешімдері койылады, оның шешімдерін келесі итерацияларға пайдаланады.

Бұл жалғасып кетебереді келесі шарт орындалғанша:

|x* - xk| <= ε

k	x1	x2	x3	x4
0	2,15	-0,83	1,16	0,44
1	2,9719	-1,0775	1,5093	-0,4326
2	2,3555	-1,0721	1,5075	-0,7317
3	3,5017	-1,0106	1,5015	-0,8111
4	3,5511	-0,9277	1,4944	-0,8321
5	3,5637	-0,9563	1,4834	-0,8298
6	3,5678	-0,9566	1,489	-0,8332
7	3,57	-0,9575	1,4889	-0,8356
8	3,5709	-0,9573	1,489	-0,8362
9	3,5712	-0,9571	1,4889	-0,8364
10	3,5713	-0,957	1,489	-0,8364

Тапсырмалар

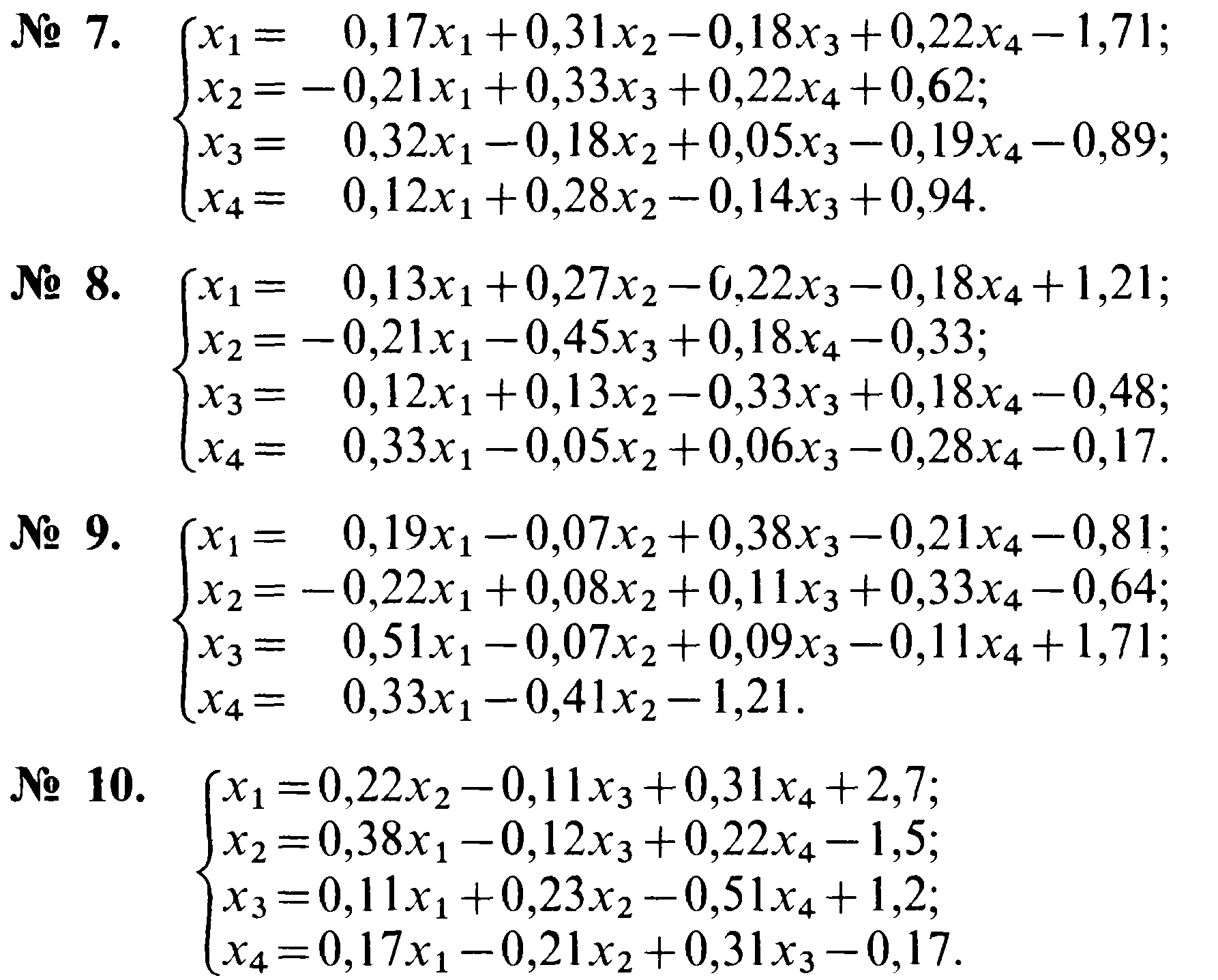
2. Зейдель әдісін қолданып сызықтық теңдеу жүйесін шешу. (ε=0,001)

Зейдель әдісінің есептеу формуларының түрлері:

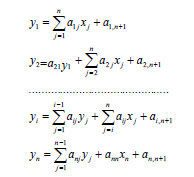
Мұндағы х₁,x₂,…,x_n – бар жуықтау элементтері, ал y₁,y₂, …,y_n – есептелетін жуықтау элементтері

Мысалы

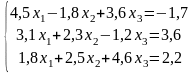
Шешу жолы:

Теңдеу жүйесін түрлендіреді, итерация әдісін тиімді пайдалану ушін

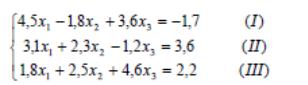
Жүйенің бас диоганальнің элементтері жолдың басқа элементтерінен кем болмайтындай түрге келтіреміз:

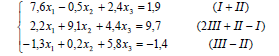
Жүйені түрлендіріп, итерацияға ыңғайлы түрге келтіреміз:

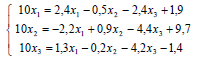
Теңдеу жүйесін MS Excel арқылы шешуге болады.

k	х1	x2	x3
0	0,19	0,97	-0,14
1	0,2207	1,0703	-0,1915
2	0,2354	1,0988	-0,2118
3	0,2424	1,1088	-0,2196
4	0,2454	1,1124	-0,2226
5	0,2467	1,1138	-0,2237
6	0,2472	1,1143	-0,2241
7	0,2474	1,1145	-0,2243
8	0,2475	1,1145	-0,2243

Тапсырмалар