Кіріспе

«Электроэнергетикадағы математикалық есептеулер және компьютерлік модельдеу» пәні 5В071800 – «Электроэнергетика» мамандықтарына арналған мамандандырылған пәндердің бірі болып табылады және 2-ші курста (4-ші семестр) оқытылады. Пәнді оқу үшін барлығы 180 академиялық сағат сабақ түрлеріне байланысты төмендегідей бөлінген: аудиториялық сағаттар саны – 60 сағат; оқытушының жетекшілігімен студенттің өзіндік жұмысы (ОСӨЖ) – 45 сағат; студенттің өзіндік жұмысы (СӨЖ) – 75 Студенттердің білімін тексерудегі қорытынды (семестрлік) бақылау түрі:– емтихан.

Пәннің саяси - ұғым бағыттылығы сапалық менеджменті жүйесін жетілдіру бойынша Қазақстан Республикасының Парламенті мен Өкіметінің ұйғарымынан шығатын талаптармен анықталады. Сапаны бақылау электр қондырғыларының есептерін математикалық тәсілмен есептеу әдістерінің негізгі түрлерінің бірі болып саналады. Техникалық аймағында әрбір жаңа эергетикалық қондырғылардың жұмыс істеу жолдарын математикалық әдістермен шешу, сондай-ақ жаңа машиналарды, құрылғыларды ойлап тапқанда, өнімнің сапасын жақсартуда және өндірудің тиімділігі кезінде де маңызды рөл атқарады.

Әрбір жаңа эергетикалық қондырғылардың жұмыс істеу жолдарын математикалық әдістермен шешу болашақта жаңа машиналарды, құрылғыларды ойлап тапқанда қателік жіберілмейді.

Тәжірибелік жұмыс №1. Сызықтық теңдеу жүйсінің шешу әдістері.

1. Крамер формуласы арқылы теңдеу жүйесін шешу.

Процедура біртекті емес n белгісізі бар n сызықты алгебралық теңдеулер жүйесін шығарады

a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1

. . . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Процедура түбірді анықтауға мүмкіндік береді, егер негізгі матрицаның анықтауышы A=(a_ij) нольге тең болмаса.

І-ші түбірді табу үшін анықтауышты іздейміз:

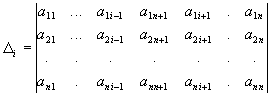
Барлық i=1..n үшін. Онда

Қорытындысында алатынымыз: егер жүйенің шешімі болмаса, онда S=0; егер жүйенің шешімі болса, онда S=1, ал массив X жүйенің шешімін құрайды. Процедурады анықтауышты есептейтін функция шақырылады, осы сапада функцияны немесе сізде бар формуланы қолдануға болады.

Мысалы:

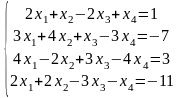
Шешу жолы:

	2	1	-2	1		0	1	0	0
	3	4	1	-3		-5	4	4	-7			-5	4	-7
|A|=	4	-2	3	-4	=	8	-2	7	-2	=	-	8	7	-2	=	-185
	2	2	-3	-1		-2	2	-1	-3			-2	-1	-3

	1	1	-2	1		0	1	0	0
	-7	4	1	-3		-11	4	9	-7			-11	9	-7
|A1|=	3	-2	3	-4	=	5	-2	-1	-2	=	-	5	-1	-2	=	-370
	-11	2	-3	-1		-13	2	1	-3			-13	1	-3

	2	1	-2	1		0	1	0	0
	3	-7	1	-3		4	-7	-13	4			4	-13	4
|A2|=	4	3	3	-4	=	7	3	9	-7	=	-	7	9	-7	=	185
	2	-11	-3	-1		-1	11	-25	10			-1	-25	10

	2	1	1	1		0	1	0	0
	3	4	-7	-3		-5	4	-11	-7			-5	-11	-7
|A3|=	4	-2	3	-4	=	8	-2	5	-2	=	-	8	5	-2	=	-555
	2	2	-11	-1		-2	2	-13	-3			-2	-13	-3

		2		1	-2		1			0		1		0		0
		3		4	1		-7			-5		4		4		-11						-5		4		-11
|A4|=		4		-2	3		3		=	8		-2		7		5			=	-		8		7		5		=			-740
		2		2	-3		-11			-2		2		-1		-13						-2		-1		-13
x1	=		|A1|			=		-370	=		2				x2		=	|A2|			=		185		=		-1
			|A|					-185										|A|					-185
x3	=		|A3|			=		-555	=		3				x4		=	|A4|			=		-740		=		4
			|A|					-185										|A|					-185

Жауабы: х₁ = 2, x₂ = -1, x₃ = 3, x₄ = 4.