§5. Диаграмма плавкости бинарной системы с химическим соединением, плавящимся инконгруэнтно

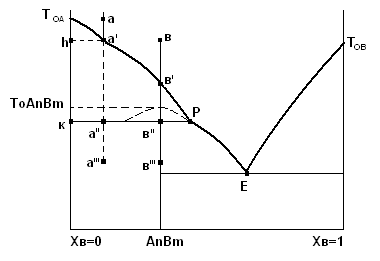
Компоненты образуют неустойчивое химическое соединение AnBm. Оно разлагается при температуре ниже своей гипотетической температуры плавления с образованием жидкости состава Р (перитектики) и кристаллов компонента А (в данном случае). Принято говорить, что такое соединение плавится инконгруэнтно.

Рассмотрим превращения в системе при движении фигуративной точки по пути а-а″′.

Устойчив расплав А – В.

С_усл. = k + 1 – ƒ = 3 – ƒ = 3 – 1 = 2.

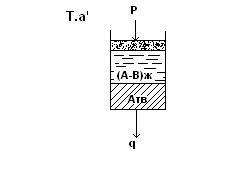
С_усл. = 3 – ƒ = 3 – 2 = 1.

При дальнейшем охлаждении фигуративная точка жидкости перемещается по линии а′Р, а фигуративная точка твердой фазы – вниз по линии hk.

В точке а″ жидкость состава Р взаимодействует с кристаллами компонента А с образованием соединения AmBn.

Ж(состава Р) + Атв AmBn

Реакция такого типа носит название перитектической.

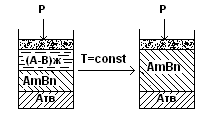
С_усл. = 3 – ƒ = 3 – 3 = 0 С_усл. = 3 – ƒ = 3 – 2 = 1

В рассматриваемом случае кристаллов А содержалось больше, чем требуется на реакцию образования AmBn (см. по правилу рычага), поэтому жидкость израсходуется вся и в фигуративной точке а′″ система будет состоять из двух твердых фаз: Атв и AmBn.

График в координатах температура – время:

Тема 4. Трёхкомпонентные системы

§1. Общие положения

Для начала отметим, что уже рассмотренные нами выше диаграммы плавкости двухкомпонентных систем с промежуточным соединением A_mB_n могли бы нами рассматриваться как трёхкомпонентные, но с добавлением r = 1. Такое добавление позволяет их классифицировать как двухкомпонентные, но число 2 тогда – число «независимых» компонентов:

С_усл = k+1–ƒ– r = (k - r) + 1 –ƒ = k´ + 1 - ƒ = (3 - 1) + 1 – ƒ = 3 – ƒ,

где k - число «независимых» компонентов.

На том этапе, который мы начинаем рассматривать, термин «трёхкомпонентные» относится к трём независимым компонентам, то есть k´ = 3 и правило фаз для прежнего условия постоянства давления запишется:

С_усл = k´ + 1 - ƒ = 3 + 1 – ƒ = 4 – ƒ.

Максимальная вариантность такой системы равна 3 (при ƒ = 1), а, следовательно, диаграмма состояния такой системы должна выражаться фигурой в пространстве. Причём, возникает проблема изображения состава трёхкомпонентной системы на плоскости.

Для изображения состава трёхкомпонентных систем чаще всего применяются треугольные диаграммы. Треугольные диаграммы строятся по методу Гиббса или методу Розебума. В каждом из этих методов используется равносторонний треугольник, вершины которого соответствуют чистым компонентам А, В, С (рисунок).

При построении треугольных диаграмм используются свойства равностороннего треугольника. Вот одно из них: сумма отрезков прямых, проведенных через любую точку, лежащую внутри равностороннего треугольника, параллельно его сторонам, есть величина постоянная, равная стороне треугольника: оα = оβ = оγ = АВ = ВС = СА. Из этого свойства следует, что точки, лежащие на прямой, параллельной одной из сторон равностороннего треугольника, изображают составы с постоянным содержанием того компонента, которому соответствует противоположная этой прямой вершина треугольника.

Метод Розебума основан на использовании свойства равностороннего треугольника, сформулированного выше. Согласно этому методу каждую сторону треугольника делят на 100 или 10 равных частей и через точки деления проводят прямые, параллельные сторонам треугольника. Длина каждой части соответствует 1% или 10%. Чтобы по этому методу указать состав трёхкомпонентной системы для фигуративной точки о, из неё проводят прямые, параллельные сторонам треугольника. Тогда массовая доля компонента А определяется длиной отрезка Сγ, компонента В – длиной отрезка Аα и компонента С – длиной отрезка Вβ. При этом длина каждого из этих отрезков будет выражена в %.

Отметим также, что фигуративная точка, лежащая на любой из сторон треугольника, отображает состав соответствующей двухкомпонентной системы.

При смешивании нескольких систем заданного состава на тройной диаграмме составов получается новая, состав которой определяется по правилу центра тяжести. Например, при смешивании двух систем, состав которых характеризуется точками a и b (рисунок) и массами m_a и m_b, фигуративная точка новой системы x будет делить отрезок ab в отношении:

т.е. по правилу рычага.

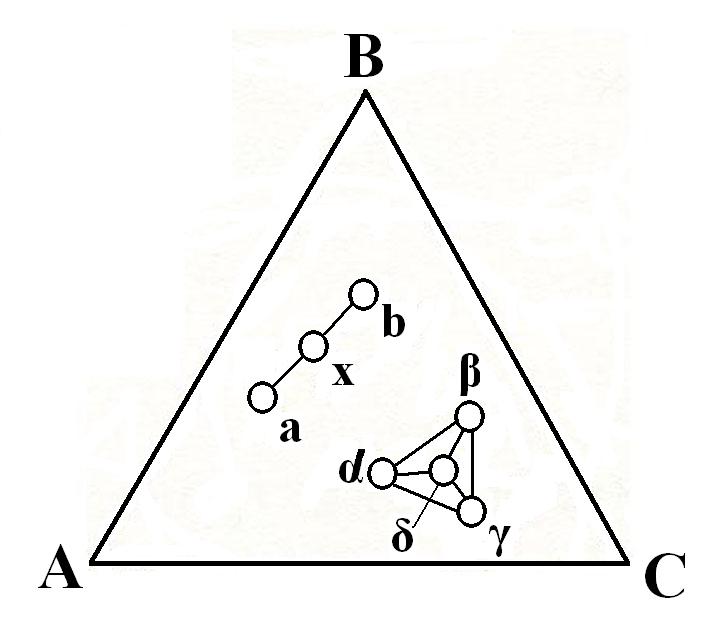
Если смешаны три системы α, β, и γ, массы которых соответственно m_a, m_b, и m_γ, то координаты фигуративной точки смеси можно определить из равенства:

m_a : m_b : m_γ = S_βγδ : S_γδα : S_αδβ,

где S – площади соответствующих треугольников.