Тема 3. Двухкомпонентные системы

§1. Общие положения

Для описания состояния двухкомпонентной системы (бинарной) необходимо указание уже трех переменных: обычно давление, температура и концентрация. Взаимосвязь трех переменных величин изображается с помощью трехмерной фигуры. Рассмотрим пример такой фигуры и геометрические образы фазовых равновесий для бинарной системы, компоненты которой в жидком состоянии образуют растворы во всей области концентрации, а в твердом состоянии вообще не растворяются один в другом.

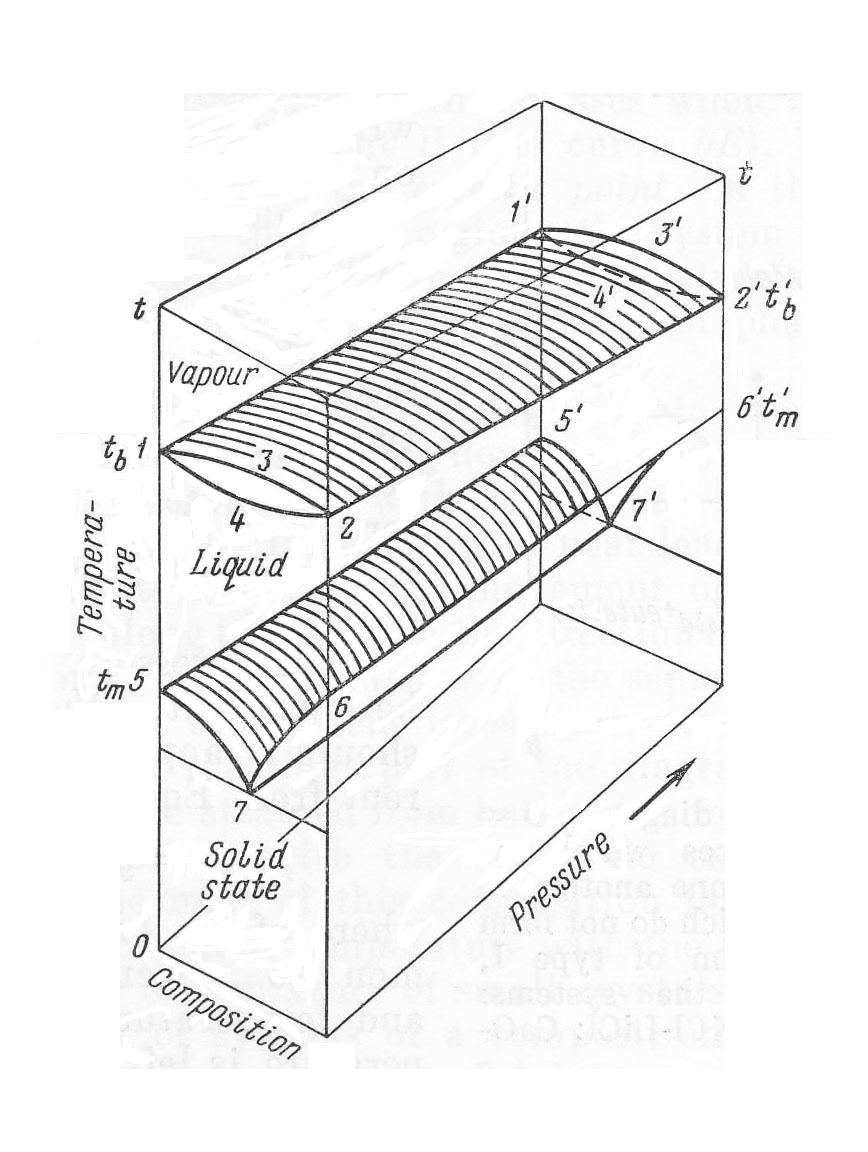
Диаграмма состояния бинарной системы с неограниченной растворимостью в жидком состоянии и полной нерастворимостью в твердом.

На рисунке изображены области трех агрегатных состояний:

I – область твердого состояния (Solid state); II – область жидкого состояния (Liquid); III – область пара (Vapour).

Применим правило фаз к любой из этих областей:

С = k + 2 – ƒ – r = 2 + 2 – 1 - 0 = 3,

т.е. произвольно можно изменять три параметра: температуру, давление и концентрацию. Точки, лежащие на линиях 11¹ и 22¹ соответствуют температурам кипения чистых компонентов при различных давлениях. Точки на линиях 55¹ и 66¹ – температуры плавления чистых компонентов в зависимости от давления.

На диаграмме можно различить ряд поверхностей.

Выпуклая поверхность 1321¹3¹2¹ выражает зависимость температуры кипения жидких растворов от состава пара и давления.

Вогнутая поверхность 1421¹4¹2¹ выражает зависимость температуры кипения от давления и состава жидкого раствора.

На поверхности 55¹77¹ жидкий расплав находится в равновесии с компонентом А.

На поверхности 676¹7¹ жидкий расплав находится в равновесии с компонентом В.

Число степеней свободы на поверхности:

С = 4 – ƒ = 4 – 2 = 2

На поверхности можно произвольно изменять только два параметра.

На линии 77¹ в равновесии находятся три фазы: жидкость, кристаллы компонента А и кристаллы компонента В.

Число степеней свободы на линии:

С = 4 – 3 = 1

Произвольно можем менять только один параметр. Два других будут являться функцией третьего.

Поскольку в интервале давлений 0÷100атм. термодинамические свойства конденсированных фаз можно считать постоянными, то обычно рассматривают не объемную диаграмму равновесия между жидкостью и твердыми фазами, а ее сечения при постоянном давлении, обычно при Р=1атм. Такие диаграммы получили название «диаграммы плавкости».

§2. Диаграмма плавкости при неограниченной растворимости в жидком состоянии и полной нерастворимости в твердом

Диаграмма плавкости для рассматриваемого примера будет иметь следующий вид:

Р = const

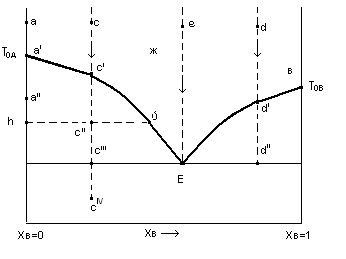
Обсудим более подробно эту диаграмму. Начнем с точки а, соответствующей чистому компоненту А в жидком состоянии. Здесь система условно обладает одной степенью свободы.

С_усл. = k+ 1 – ƒ = 2 – 1 = 1

При отводе теплоты от системы жидкость охлаждается и фигуративная точка на диаграмме перемещается вниз до точка а′, в которой начнется кристаллизация жидкого компонента А при постоянной температуре Т_ОА.

С_усл. = 2 – ƒ = 2 – 2 = 0 С_усл. = 2 – ƒ = 2 – 1 = 1

После этого потеря теплоты будет связана с понижением температуры и фигуративная точка системы движется в направлении а″, что означает охлаждение уже твердого А.

Изобразим процесс охлаждения в координатах температура – время.

Если к жидкому компоненту А добавить растворимый в нем компонент В, то температура начала кристаллизации компонента А из расплава (А-B)_ж будет ниже температуры кристаллизации чистого А. Это является следствием из закона Рауля, который будет рассматривается в разделе «Растворы» учебной дисциплины «Физическая химия». Кривая а′Е отражает это понижение. Равным образом понижается температура начала кристаллизации и в том случае, если к жидкому компоненту В добавлять компонент А (кривая вЕ). Обе кривые пересекаются в точке Е, называемой эвтектической.

В области над кривыми – в области расплава – система имеет условно две степени свободы:

С_усл. = k + 1 – ƒ = 2 + 1 – 1 = 2,

т.е. здесь произвольно можно изменять и температуру и состав, а число фаз (одна) будет оставаться постоянным. Линия аЕв – линия ликвидуса. Возьмем в области реализации жидкого состояния фигуративную точку с и рассмотрим последовательность превращений в системе при движении ее вниз.

С_усл. = 2 + 1– 1 = 2

При отводе теплоты такой системы достигается состояние с′, где расплав насыщен компонентом А и он начинает выделяться в чистом виде.

С_усл. = к + 1 – ƒ = 3 – ƒ = 3 – 2 = 1

Т = ƒ(Х₁) и Х = ƒ(Т) связаны уравнением Шредера.

Система становится моновариантной и при дальнейшем отводе теплоты понижение температуры сопровождается дальнейшей кристаллизацией компонента А и одновременно изменением состава остающегося раствора по линии с′Е в направлении точки Е. При этом фигуративной точке всей системы отвечают две фигуративные точки каждой из фаз, например, точке с″ отвечают точки h и ύ. Фигуративная точка твердой фазы опускается по вертикали. Фигуративная точка расплава перемещается по кривой с′Е. Точки

h и ύ называются сопряженными, а линия h с″ ύ – коннодой. Существует правило, которое носит название «правило рычага»: фигуративная точка всей системы делит проходящую через нее конноду на отрезки, обратно пропорциональные массам фаз, на которые распадается равновесная система, т.е. для фигуративной точки с″:

Вариантность в точке с″ такая же, как и в точке с′: С_усл =3–ƒ = 3–2 = 1.

Аналогичные явления, только связанные с выделением компонента В происходят при отводе от системы теплоты для точек в правой части диаграммы (например d). Когда фигуративная точка системы достигает положения с′″, фигуративная точка жидкости попадает в Е. В эвтектической точке Е, которая может быть достигнута с обеих сторон, расплав состава Е может находиться в равновесии с обоими твердыми компонентами А и В.

С_усл =3–ƒ = 3–3 = 0

При постоянной температуре смесь мелких кристаллов компонентов А и В начинает выпадать одновременно, образуя твердую эвтектику.

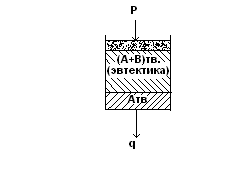
Эвтектика не представляет собой самостоятельную фазу. Фазы здесь две: А_тв и В_тв.

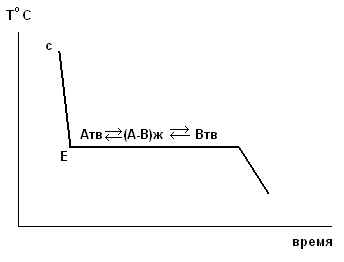
На графике в координатах температура – время процесс кристаллизации сплава выглядит следующим образом:

Принципиальное отличие в механизме кристаллизации сплава по сравнению с чистым веществом заключается в том, что сплав кристаллизуется в интервале температур с′ - с′′′). Температура Тс′ - температура начала кристаллизации сплава.

Существует единственный сплав, который будет кристаллизоваться как чистое индивидуальное вещество. Его состав отвечает составу эвтектики.

При рассмотрении процессов в двухкомпонентной системе (при кристаллизации) возникает вопрос: почему не вводим ограничение

x = const, когда фигуративная точка движется вниз? Поскольку в однокомпонентной системе вводилось ограничение: Р = const или

Т = const при движении фигуративной точки вправо или вниз. Ответ, по-видимому, должен быть таким: в однокомпонентных системах, принимая постоянство давления и ограничивая число степеней свободы, мы беремся такое постоянство поддерживать (например, используем цилиндр с поршнем, имеющим постоянное давление). В случае двухкомпонентной системы мы не ставим задачу поддерживать х = const и не принимаем для этого никаких мер. В самом деле: состав жидкой фазы при понижении температуры будет изменяться по уравнению Шредера.