§ 3 Условная вариантность.

Вариантность системы при условии постоянства некоторого числа переменных или соотношений между переменными называется условной. С_усл. – условная вариантность. Общее число переменных:

t = k∙ƒ + 2.

Наиболее часто накладываемое условие на систему – постоянство давления. Оно оправдано при рассмотрении равновесий между конденсированными фазами, термодинамические свойства которых, как мы знаем, слабо от него зависят. В этом случае:

t = k∙ƒ + 1, и

С_усл = k + 1 – ƒ – r. (15)

Если ограничение для системы будет такое: ,

то t = k∙ƒ и

С_усл = k – ƒ – r. (16)

В общем случае, если на систему накладывается l ограничений, то правило фаз принимает вид:

С_усл = k + 2 – ƒ – r – 1. (17)

В количественном соотношении всегда

С_усл < С. (18)

Тема 2. Однокомпонентные системы

§1. Общие положения

Равновесие однокомпонентной системы определяется только внешними параметрами Р и Т, поскольку внутренних - нет.

Если система однокомпонентная, то число химических реакций r = 0. Тогда:

С = k + 2 – ƒ – r = 3 – ƒ. (19)

Отсюда следует зависимость вариантности от числа фаз, находящихся в равновесии. Чем больше число фаз в равновесии, тем меньше вариантность. Установим наибольшую и наименьшую вариантность.

Наибольшая вариантность:

С_наиб = 3 – 1 = 2.

Наибольшей вариантности соответствует наименьшее число фаз, находящихся в равновесии – 1.

Наименьшая вариантность:

С_наим = 3 – 3 = 0.

Наименьшей вариантности отвечает наибольшее число фаз, находящихся в равновесии – 3. То есть в любой однокомпонентной системе не может одновременно находиться в состоянии равновесия более 3 – х фаз.

§2. Равновесие двух фаз однокомпонентной системы.

Уравнение Клапейрона – Клаузиуса

Подставим в правило фаз Гиббса для однокомпонентной системы ƒ = 2. Тогда: С = 3 - ƒ = 1. Это означает, что при равновесии двух фаз в однокомпонентной системе только один из внешних параметров может принимать произвольные значения, а другой должен быть при этом строго определённым, иначе равновесие материализоваться не будет (в ограниченном интервале температур и давлений возможны метастабильные состояния). То есть: Р = ƒ(T) или Т = ƒ(Р). В явном виде обсуждаемая зависимость известна как уравнение Клапейрона – Клаузиуса:

, (20)

где ∆H – молярное изменение энтальпии при переходе от одной сосуществующей фазы к другой, кДж/моль; (V₂ – V₁) – изменение молярных объёмов при переходе от одной сосуществующей фазы к другой л/моль.

§3. Диаграммы состояния однокомпонентных систем

Диаграмма состояния – это график в определённых координатах, на котором изображены возможные состояния многофазной и многокомпонентной системы. Точка, отвечающая состоянию системы на этой диаграмме, называется фигуративной. С одной из диаграмм состояния – диаграммой состояния воды, мы уже знакомы. Сейчас посмотрим на нее в несколько ином плане.

Диаграмма состояния воды.

Диаграмма состояния однокомпонентной системы изображается в координатах Р и Т.

Точка «О», отвечающая равновесию трех фаз на диаграмме, называется «тройной точкой». Для нее:

С = 3 – ƒ = 3 – 3 = 0.

Поэтому она характеризуется вполне определенными значениями температуры и давления (Т = 273,16К, Р = 0,006атм.).

Линия АО – линия равновесных состояний двухфазной системы

лед пар

С = 3 – 2 = 1.

Линия АО начинается, как можно считать, при абсолютном нуле.

Линия ОВ – линия равновесных состояний двухфазной системы

жидкость пар

С = 3 – 2 = 1.

Точка В имеет координаты: T = 374⁰С; P = 220атм).

Линия ОС – линия равновесных состояний двухфазной системы

тв. вещество жидкость

С = 3 – 2 = 1.

Поле I - область равновесного состояния льда

С = 3 – 1 = 2.

Поле II - область равновесного состояния жидкой воды

С = 3 – 1 = 2.

Поле III - область равновесного состояния пара

С = 3 – 1 = 2.

Рассмотрим последовательность превращений в системе при движении фигуративной точки по горизонтальной прямой от положения x до положения y.

В точке х при давлении 1 атм и температуре Т₁ устойчив лед.

Подсчитаем вариантность в этой точке. Поскольку на систему накладывается ограничение Р = 1атм, то вариантность будет условной:

С_усл = 2 – ƒ = 1,

т. е. произвольно можно изменять один параметр – температуру.

Продвижение по горизонтали вправо означает нагревание льда, продолжающееся до точки n. Здесь происходит фазовый переход

л ед вода, появляется новая фаза и условная вариантность

С_усл = 2 – 2 = 0

Следовательно, температура будет оставаться постоянной, пока лед полностью не расплавится и система снова не станет однофазной. После чего температуру теперь уже жидкой воды снова можно повышать до точки m. В точке m вода закипит при 100⁰С, и эта температура будет оставаться постоянной, пока вся вода не превратится в пар, который дальше будет нагреваться до температуры Т₂. С_усл = 2 – 2 = 0

Нагреваться от точки m до y будет уже пар.

Путь системы от состояния, отмеченного фигуративной точкой х до состояния, отмеченного фигуративной точкой у можно изобразить на графике температура-время:

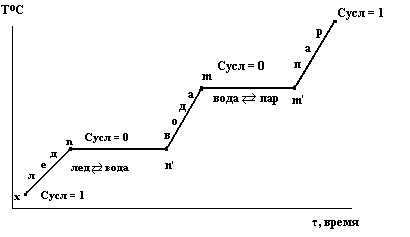
Полностью плавление индивидуального вещества происходит при постоянной температуре.

Диаграмма состояния железа

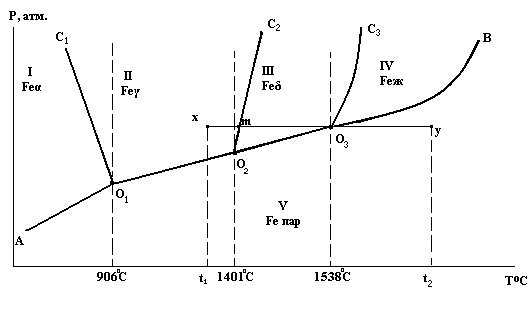
Fe_α - объемноцентрированный куб (ОЦК).

Fe_γ - гранецентрированный куб (ГЦК).

Fe_δ - объемноцентрированный куб (ОЦК).

О₁, О₂, О₃ – тройные точки на диаграмме, здесь в равновесии находятся три фазы:

О ₁ - Fe_α Fe_γ Fe_пар

О₂ - Fe_γ Fe_δ Fe_пар С = 0

О₃ - Fe_δ Fe_ж Fe_пар

Параметры Р и Т имеют строго определенное значение.

Линии ни диаграмме отвечают равновесию двух фаз:

А О₁ - Fe_α Fe_пар

О ₁С₁ - Fe_α Fe_γ

О ₁О₂ - Fe_γ Fe_пар

О ₂С₂ - Fe_γ Fe_δ С = 3 – 2 = 1

О ₂О₃ - Fe_δ Fe_пар

О ₃С₃ - Fe_δ Fe_ж

О ₃В - Fe_ж Fe_пар

Можно произвольно изменять один параметр, не изменяя числа фаз, находящихся в равновесии.

Области на диаграмме отвечают устойчивому состоянию одной фазы.

I - устойчиво Fe_α

II - устойчиво Fe_γ

III - устойчиво Fe_δ С = 3 – 1 = 2

IV - устойчиво Fe_ж

V - устойчиво Fe_пар

Система бивариантна, можно изменять два параметра Р и Т.

Рассмотрим последовательность превращений в системе при движении фигуративной точки по горизонтальной прямой от положения х до положения у, что соответствует изобарическому нагреванию железа.

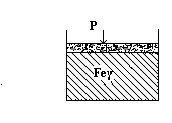
В точке х устойчиво Fe_γ. С_усл = 2 – ƒ = 2 – 1 = 1

Нагревание Fe_γ при давлении Р приводит нас в состояние, отмеченное на диаграмме фигуративной точкой m. Появляется новая фаза - Fe_δ и вариантность изменяется: С_усл = 2 – ƒ = 2 – 2 = 0

Дальнейший подвод теплоты приводит к исчезновению Fe_γ при постоянной температуре.

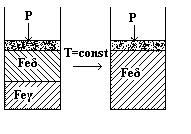
Далее нагревается уже Fe_δ и фигуративная точка, перемещаясь вправо, попадает в точку О_3. Точка О₃ отвечает равновесию трех фаз:

Fe_δ Fe_ж Fe_пар

Однако при Р = const образование сразу двух новых фаз: жидкости и пара невозможно, т.к. С_усл = 2 – ƒ = 0 и ƒ_max = 2; в равновесии могут находиться только две фазы. Поэтому последовательность превращений в точке О₃ будет такова:

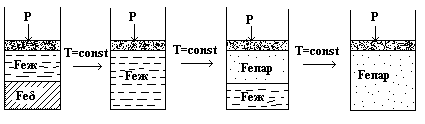
на короткое время

От точки О₃ до точки у нагреваться до температуры Т₂ будет уже пар.

Путь сиcтемы xmO₃y в координатах температура – время можно изобразить следующим образом:

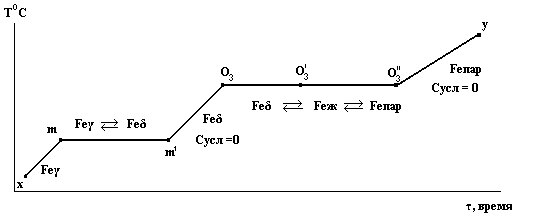
Диаграмма состояния серы

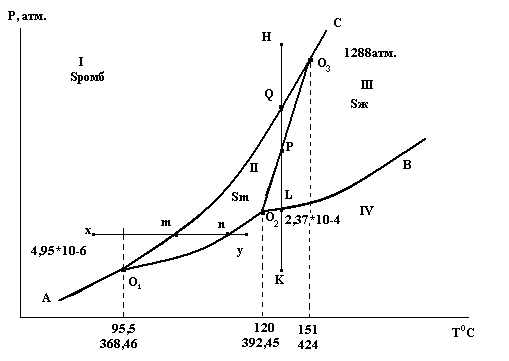
Сера существует в двух устойчивых кристаллических модификациях:

ромбической (S_ромб) и моноклинной (S_м).

О₁, О₂, О₃ – тройные точки на диаграмме. Здесь в равновесии находятся три фазы.

О ₁ - S_ромб S_м S_пар

О ₂ - S_м S_ж S_пар С = 3 – ƒ = 3 – 3 = 0

О ₃ - S_ромб S_м S_ж

Давление и температура имеют строго определенное значение.

В точке О₃ в равновесии находятся все конденсированные фазы.

Линии на диаграмме отвечают равновесию двух фаз.

А О₁ - S_ромб S_пар О₁О₃ - S_ромб S_м

О ₁О₂ - S_м S_пар О₂О₃ - S_м S_ж

О ₂В - S_м S_пар О₃С - S_ромб S_ж

Вариантность на линии: С = 3 – ƒ = 3 – 2 = 1

Области на диаграмме (поля) отвечают устойчивому состоянию одной фазы.

I - устойчива S_ромб

II - устойчива S_м С = 3 – ƒ = 3 – 1 = 2

III - устойчива S_ж

IV - устойчива S_пар

Рассмотрим последовательность превращений при движении фигуративной точки от положения х до положения у, что соответствует изобарическому нагреванию серы.

В точке х устойчива ромбическая сера. С_усл. = 2 – ƒ = 2 – 1 = 1

Нагревание S_ромб приводит нас в состояние, которому отвечает фигуративная точка m. Появляется новая фаза – сера моноклинная.

С_усл. = 2 – ƒ = 2 – 2 = 0

Температура будет оставаться постоянной, пока ромбическая сера полностью не перейдет в моноклинную.

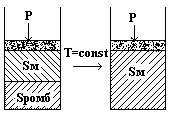
При дальнейшем подводе теплоты температура моноклинной серы будет повышаться, и система придет в состояние n, где появится новая фаза - S_пар. Система снова станет инвариантной до полного испарения.

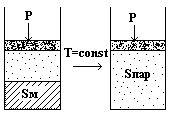
В дальнейшем, до точки у будет нагреваться уже пар серы.

В рассмотренном примере превращение твердого вещества в пар произошло, минуя жидкое состояние.

График в координатах температура – время:

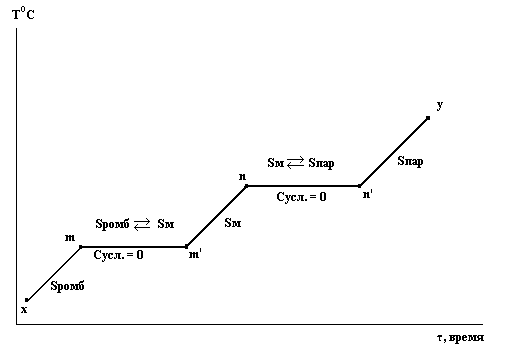
Рассмотренные примеры изобарических превращений H₂O, Fe, S дают представления о том, как строятся диаграммы состояния однокомпонентных систем. Имея совокупность графиков в координатах температура – время, при подводе или отводе теплоты для различных давлений, и взяв из них температуры остановок (площадок), можно установить положение линий на диаграмме и координаты тройных точек.

Теперь рассмотрим последовательность превращений в сере при движении фигуративной точки от положения К в положение Н, что соответствует изотермическому сжатию.

В точке К устойчив пар. С_усл. = 2 – ƒ = 2 – 1 = 1

Увеличивая давление, попадаем в точку L, где пар начинает конденсироваться в жидкость. С_усл. = 2 – ƒ = 2 – 2 = 0.

Следовательно, конденсация будет происходить при постоянном давлении, пока весь пар не превратится в жидкую серу.

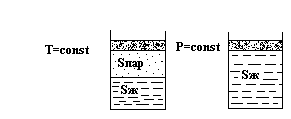
Система станет моновариантной и давление жидкости можно повышать до точки Р. Здесь из жидкости начнут выпадать кристаллы моноклинной серы и давление будет оставаться постоянным до полной кристаллизации:

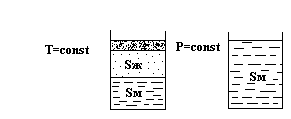
При более высоком давлении в точке Q моноклинная сера начнет переходить в ромбическую. Давление при этом тоже будет оставаться постоянным.

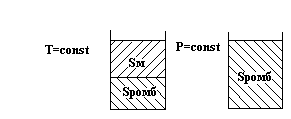
От точки Q до H точки сжиматься будет уже ромбическая сера.

График в координатах давление – время: