4.11. Уравнения изопроцессов. Работа газа.

Изопроцессы – термодинамические процессы, во время которых количество вещества и параметры состояния: давление, объем или температура остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объему – изохорный, температуре – изотермический, энтропии – изоэнтропийный. Изобарный процесс – процесс изменения состояния термодинамической системы при постоянном давлении V/T = const. Изохорный процесс – P/T = const. Изотермический процесс – PV=const. Изоэнтропийный процесс - pV^ϒ=const.

Работа газа при его расширении в цилиндре с поршнем (поршень поднимается на величину dx, S – площадь поршня): δА = PdV. Эта величина является элементарной работой газа. Работа при расширении газа от объема V₁ до V₂ будет равна: А₁₂ = ∫^V1_V2 PdV. Теплоемкость тела – физическая величина, определяющая отношение безконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению температуры δТ. С = δQ/ δТ [Дж/К]

Внутренняя энергия системы может меняться за счет энергии, сообщаемой системе извне, посредством двух процессов: либо за счет работы, производимой внешними силами над системой, либо за счет передачи ей тепла. При соприкосновении тел либо при взаимодействии тел через излучение, изменение внутренней энергии происходит за счет передачи энергии (теплоты) хаотически движущихся частиц одного тела частицам другого. Связь между переданным теплом, изменением внутренней энергии системы и произведенной работой выражается уравнением: dQ = dE + dA = dE + PdV – первое начало термодинамики.

Энтропия системы является функцией состояния, определенная с точностью до произвольной постоянной. Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии

.

       Таким образом, по формуле можно определить энтропию лишь с точностью до аддитивной постоянной, т.е. начало энтропии произвольно. Физический смысл имеет лишь разность энтропий.         Каждый из изопроцессов идеального газа характеризуется своим изменением энтропии, а именно:

изохорический:   , т.к.  ;

изобарический:   т.к. Р₁ = Р₂;

изотермический:   т.к.  ;

адиабатический:   , т.к. 

4.12. Круговые процессы.

Процесс, при котором система переходит из состояния 1 в состояние 2, а затем возвращается в состояние 1 через другие промежуточные процессы, называется круговым процессом или циклом. Графически цикл изображается замкнутой кривой.

Всякая тепловая машина представляет собой систему, совершающую много кратно некий круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объёма , а затем сжимается до первоначального объёма (рис. 1). Чтобы работа за цикл была больше нуля, давление, (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать теплоту, а в ходе сжатия отнимать от него теплоту. Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемой рабочему телу за цикл, равно , где – теплота, получаемая рабочим телом при расширении, а – теплота, отдаваемая при сжатии. Работа , совершаемая за цикл, равна площади цикла. Таким образом, первое начало термодинамики, написанное для цикла, имеет вид . Как следует из этого выражения, не вся получаемая извне теплота используется для получения полезной работы.

Коэффициентом полезного действия (сокращённо КПД) тепловой машины называется отношение совершаемой за цикл работы к полученной за цикл теплоте .

Цикл Карно и его КПД Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е. . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно. - изотермическое расширение при , - адиабатическое расширение, 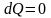, - изотермическое сжатие при , - изотермическое сжатие, .

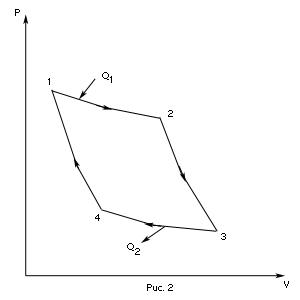П ри изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты равно работе 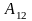, совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна

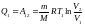, где – масса идеального газа в тепловой машине

формула для КПД цикла Карно: , где - температура нагревателя, - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах и .