Вопрос 1.1Механическое движение. Траектория движения. Пройденный путь. Скорость, ускорение движения. Механика-это раздел физики, в котором изучается механическое движение. Механическое движение это изменение со временем положения тел или их частей друг относительно друга. Движение тел со скоростью света в вакууме изучает классическая механика. В ней состояние тел в выбранный момент времени определяются быстротой их движения. Задача механики-определить состояние тела в любой момент времени. Состояние тела определяется положением тела и его скоростью. Движение любой частицы можно описать естественным способом: указать траекторию её движения и пройденный ею путь. Траектория-воображаемая линия, по которой движется частица. Пройденный путь-длина участка территории, пройденного частицей к данному моменту времени. В этом случае при заданной траектории движения частицы описывается зависимостью пройденного пути L от времени t: L=L(t). 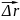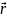Перемещение (Δr)-изменение радиуса вектора движущейся точки за промежуток времени движения ≤ ΔL Δr= (t₂)- (t₁) Скорость-это характеристика быстроты изменения перемещении V_ср= , =Lim = , скорость равна первой производной от радиус вектора по времени , = * = * V= -модуль скорости. Скорость направлена по касательной к траетории х=A+Bt+C²t² V_x=0+B+2C²t Различают среднюю и мгновенную скорости. Ускорение – характеристика быстроты изменения скорости. Это предел отношения изменения скорости к промежутку времени, за которое это изменение произошло, когда Ускорение равно первой производной от скорости во времени =Lim = 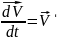, 1) =0 –равномерное прямолинейное движение =const (а_τ =а_n=0) = + t , 2) -равноускоренное движение , V=V₀+at, r=r₀+V₀t+at²/2, a=a_n+a_τ . Ускорение движения принято раскладывать на две составляющие: нормальную a_n (вдоль нормали n),направленную перпендикулярно скорости и касательной к траектории, и тангенциальную a_τ, направленную вдоль скорости и касательной к траектории движения. Тангенциальное ускорение-характеризует быстроту изменения модуля скорости a_τ= , нормальное ускорение направлено к центру кривизны траектории и характеризует быстроту изменения скорости по направлению a_n=

Вопрос 1.2 Законы Ньютона. Силы в механике. Первый закон Ньютона: тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не изменит это состояние. Закон устанавливает, когда движение тела не изменяется. Под изменением движением тела подразумевается изменение скорости движения, т.е. движения с ускорением. Второй закон: В инерциальных системах отсчета произведение массы тела на ускорение его движения равно действующей на тело силе F=ma. В инерциальных системах отсчета скорость изменения импульса тела равна действующей на тело силе 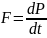. Инерциальная система отсчета-это система отсчета, в которой выполняется 1 закон Ньютона. Третий закон: силы взаимодействия тел равны по модулю, противоположны по направлению, приложены к разным телам, одинаковы по природе и принадлежат одной прямой F₁₂=-F₂₁. Сила всемирного тяготения (сила гравитационного взаимодействия частиц) Тело массой m и Земля с силой тяготения притягиваются. G-гравитационная постоянная. Сила тяжести F_T=mg, ускорение которое сообщает телу сила, является ускорением свободного падения. Вес тела P=m(g-a ), сила упругости (сила Гука ) F=-k* , сила архимеда (выталкивающая сила) F= , сила Стокса(сила сопротивления при малых скоростях) F=αV.

Вопрос 1.3 Кинематика движения точки по окружности. При движении точки по окружности за начало координат обычно принимают центр окружности С;радиус-вектор движущейся точки R; положение точки вместо трех координат x, y, z задается плоскостью, в которой лежит траектория, радиусом окружности и углом между радиусом-вектором точки и выбранной осью в плоскости вращения (х). При движении точки по окружности и вращательное движение твердых тел характеризуется: углом поворота Δφ, угловой скоростью ⍵, вектором угловой скорости , угловым ускорением При движении точки по окружности плоскость вращения. И радиус окружности со временем не изменяется, поэтому Движение описывается зависимостью φ (t)

1)угол поворота Δφ-это угол, на который поворачивается радиус-вектор R точки за время Δt. Δφ=ΔL/R

2)угловая скорость-характеристика быстроты движения точки ω=φ =dφ/dt; -вектор угловой скорости направлен по оси вращения по правилу правого угла.V=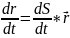 V=R*ω 3)угловое ускорение-характеристика быстроты изменения вектора угловой скорости со временем α= = ω

-замедленное движение, -ускоренное движение, -равномерное движение.

Связь линейной скорости и угловой: V=ΔL/Δt , ω=Δφ/Δt, V=ω*R. Связь тангенциального ускорения с угловым: a_τ=α*R , a_n=-ω²*R. Вращательным называется движение твердого тела, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. При вращении все точки твердого тела движутся по окружности, поэтому вращение твердого описывается также, как и движение точки по окружности. При вращательном движении разные точки твердого тела будут двигаться по окружностям разных радиусов с разными линейными скоростями и ускорениями. При этом угловые скорости и угловые ускорения всех точек твердого тела будут одинаковыми.

Вопрос 1.4 Динамика вращательного движения тел вокруг неподвижной оси. Абсолютно-твердое тело-это тело, деформациями которого можно пренебречь в условиях данной задачи. При вращательном движении твердых тел для их отдельных частиц в результате неоднородной деформации возникает сила. Чем дальше расположены части твердого тела от оси вращения, тем меньше деформации. Для хар-ки действия силы, ускоряющей вращение тел, вводится векторная величина-момент силы . Момент силы-это векторное произведение радиуса-вектора, соединяющего О с точкой приложения силы на силу. ={r*F} относительно точки О. Плечо силы-это кратчайшее расстояние от точки О до линии действия силы. Момент инерции тела относительно произвольной оси равен произведению массы тела на квадрат его расстояния до оси вращения Y=m*R². Момент инерции системы сил равен сумме моментов инерции каждой материальной в отдельности Y= _I , Y= * . Скорость изменения момента импульса тела со временем равна результирующему моменту сил, действующих на тело. =dL/dt-осн.закон динамики вращательного движения. L_z=J*ω- момент импульса относительно неподвижной оси.

Вопрос 1.5Импульс тела. Закон сохранения импульса. Импульс тела-произведение массы тела на его скорость. Закон сохранения импульса: при взаимодействиях тел изолированной системы тел сохраняется =const , p=m*v. Импульс системы сохраняется если она изолирована и если система не изолирована, но сумма внешних сил равна нулю.dP/dt=F_внеш+F_внутр , _внеш=0. Момент импульса тела относительно оси. Основное ур-ние динамики вращательного движения:

dL₁/dt=M_1внеш+M_1внутр , Если система изолирована, то сумма моментов внешних сил равна 0, L_c=const, dL_c/dt= _iвнеш. Момент импульса изолированной системы есть система постоянная М_внеш=0, то L_1x+L_2x+…= + +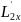… Если результирующий момент внешних сил на ось равен нулю, то сохраняется проекция суммарного импульса на эту ось. Закон сохранения импульса проявляется везде, где есть вращение.

Вопрос 1.6 Работа силы. Консервативные и неконсервативные силы. Работа силы-это скалярная величина, которая вводится для хар-ки результата действия силы на тело, вызывающей перемещение этого тела. Элементарной работой силы называется скалярное произведение силы на перемещение d , которое совершает точка приложения силы: dA=F d Учитывая , что F d α, А dr=dL получим A=F*Δr* α, Δr-перемещение Если α>0, A>0 Если α<0, A<0

Работа силы трения всегда отрицательна А=0,если α=0 (⍺=90◦). Работа центростремительной силы А=0

Работа силы тяжести А_mg=mg(h₁-h₂), эта работа не зависит от траектории, а определяется только начальным и конечным положением тела. Силы, работа которых не зависит от траектории, называются консервативными силами.(сила тяжести, сила упругости), или работа которых на любом замкнутом пути равна нулю. F_упр=-kx A_упр=k /2- k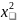 /2 . Потенциальная энергия обусловлена консервативным взаимодействием тел. Система тел обладает потенциальной энергией только в том случае, если силы, действующие в системе-консервативные. Свойства: зависит от взаимного расположения тел (W_n(x,y,z,t)); ноль отсчета потенциальной энергии выбирается произвольно; физический смысл имеет изменение потенциальной энергии ΔW_п=-Аконс, А_mg=mgh₁-mgh₂ , Aконс=W_п1-W_п2. Для силы тяжести W_п=mgh, а для силы упругости W_п=kx²/2

Кинетическая энергия обусловлена движением тела W_к=mv²/2, кинетическая энергия численно равна работе, которую надо совершить, чтобы увеличить скорость тела от 0 до v. Если на тело действуют несколько сил, то используют теорему: ΔWк= сумма работ всех сил, действующих на тело. Изменение кинет.энергии тела равно алгебраической сумме работ всех сил действующих на тело ΔW_к=W_к1-W_к2. Кинетическая энергия вращ.движения: m_i-элементарный участок W_кi= /2= /2 , V_i=ω_i*r_i тогда W_кi= ω²/2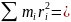 Jω²/2 , Jω²/2= W_к , W_к= mv²/2+ Jω²/2 (и поступательного и вращательного)

Вопрос 1.7 Механическая энергия. Закон сохранения механической энергии. Механическая энергия это сумма кинетической энергии и потенциальной. W_мех=W_к+W_п . Закон сохранения механической энергии является частным случаем закона сохранения энергии. Пусть F₂ и F₃ – консервативные силы, тогда теорема о кинет.энергии для этого тела равна W_к=А₁+А₂+А₃+…, А_конс=-Δ W_п

ΔW_к+ΔW_п= А₁+А₄-неконсервативные силы , ΔW_мех=А_неконс. Изменение механической энергии тела равно сумме работ всех неконсервативных сил, действующих на тело. Если на тело действуют только консервативные силы, то его механическая энергия остается величиной постоянной. Закон сохранения мех.энергии выполняется как для замкнутых, так и не для замкнутых систем, если внутренние и внешние силы консервативны. Сила трения, и сопротивления - являются неконсервативными силами(или диссипативными).

Вопрос 2.1 Электрическое взаимодействие заряженных тел. Все тела в природе способны электризоваться, т.е приобретать электрический заряд. Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами. Имеются два вида электр.зарядов, условно называемых положительными и отрицательными. Заряды одного знака отталкиваются, а одноименного-притягиваются друг к другу. Элементарный заряд-заряд всех элементарных частиц, одинаковый по абсолютной величине. Электрический заряд является неотъемлимым свойством некоторых элементарных частиц (электроны, протоны, нейтроны). Закон Кулона: сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между F=k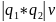 r² . Электростатическое поле-это материя, которая окружает покоящиеся электрические заряды и оказывает электростатическое воздействие на другие заряды. Электрическое поле – поле, через которое осуществляется взаимодействие между покоящимися зарядами. Проявляет себя в том, что помещенный в какую-либо его точку электрический заряд оказывается под действием силы. Напряженностью электр.поля называется величина показывающая, с какой силой электрическое поле действует на единичный положительный точечный заряд = /q. Потенциал-энергетическая хар-ка, показывающая какую потенциальную энергию имеет положительный единичный точечный заряд вследствие действия электростатического поля =W_п/q. Система тел, в которой действуют консервативные силы обладают потенциальной энергией Δ W_п=- А_конс . Потенциал в данной точке поля равен отношению потенциальной энергии точечного заряда, помещенного в эту точку поля, к величине заряда. Работа сил электрического поля по перемещению заряда q из точки 1 в точку 2 равна произведению этого заряда на разность потенциалов A_эл=q(φ₁-φ₂)

Вопрос 2.3 Электрический ток. Сила тока. Плотность тока. Электрический ток – направленное (упорядоченное) движение заряженных частиц. Это движение создается при помощи электрического поля, которое совершает определенную работу. Это явление называется работой электрического тока. Для того, чтобы переместить большой заряд по электрической цепи за одну секунду, электрическое поле должно выполнить большую работу. Следует, что работа элю тока должна зависеть от силы тока. Сила тока – количественная характеристика равная отношению заряда dq проходящего через поперечное сечение проводника за некоторый промежуток времени dt. J=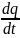 Единица силы тока в СИ – А (ампер). Если сила тока и его направление со временем не изменяются, то ток называется постоянным.

Плотность тока (j) – это векторная физическая величина, модуль которой равен отношению силы тока в проводнике к площади поперечного сечения проводника. j= (А/м²). Любой источник тока характеризую электродвижущей силой. ЭДС – физическая скалярная величина численно равная работе сторонних сил по перемещению единичного положительного заряда внутри источника тока. ε=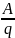 (В) вольт.

Напряжение – это отношение работы тока на определенном участке электрической цепи к заряду, протекающему по этому же участку цепи. Измеряется в вольтах (Дж/Кл) U=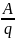

Закон Ома: сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения на проводнике. J= (R – электрическое сопротивление проводника). Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении в 1В течет ток силой 1А. Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника R= (l – проводника, S – площадь поперечного сечения, ). Закон Ома в дифференциальной форме: плотность тока i=

Закон Джоуля-Ленца: В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается, т.е. при протекании тока в проводнике выделяется тепло. Q=U*J*t

Следовательно, из закона Ома U заменили и получили формулу: Q=R*J²*t

Электрический ток в металлах: все металлы в твердом и жидком состоянии являются проводниками электрического тока. проводник – это тело, внутри которого содержится достаточное количество свободных электрических зарядов, способных перемещаться под действием электрического поля. В металле всегда существует большое количество свободных электронов. Электрический ток в металлических проводниках – это упорядоченное движение свободных электронов под действием эл. Поля, создаваемого источником тока.

Вопрос 2.4 Магнитное взаимодействие. Индукция и напряженность магнитного поля. Взаимодействие токов осуществляется через поле, называемое магнитным. Магнитное поле создаётся движущимися зарядами. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Магнитное поле не действует на покоящиеся заряды. Направление вектора магнитной индукции совпадает с направлением северного конца магнитной стрелки, совпадает с нормалью к контуру с током. (1 Тл=1Н/А). Линии касательные, которые в каждой точке совпадают с направлением вектора , называются линиями магнитной индукции. В однородном поле : линии имеют вид концентрических окружностей, направление определяется по правилу правой руки. Закон Био-Савара-Лапласа: dB=μμ₀Y(dL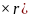 /4πr³ , где dL-элементарный участок проводника с током, L совпадает с направлением Y, r-вектор, проведенный от элемент.участка в данную точку, dB-магнитная индукция, создаваемая элементом тока Y dL. Направление магнитной индукции находится по правилу правой руки и вырезанием участка dL.Индукция прямого проводника с током : B= μμ₀Y/4πr₀(cosα₁-cosα₂), индукция соленоида: B= μμ₀Yn, где n-число витков на единицу длины. Закон Ампера: На проводник с током, помещенный в магнитное поле действует сила, которая несет название сила Ампера d _A=Y и она равна произведению силы тока на векторное произведение dl на B. Dl-элемент длины проводника, направленный по направлению тока.Если магнитное поле однородно, а проводник прямолинейный, то сила Ампера будет равна _A=YВLsinα; В численно равна силе, с которой действует однородное магнитное поле на прямой проводник длиною в 1 м,по которому течет ток в 1А и который расположен перпендикулярно линиям магнитной индукции. Сила Лоренца-это сила, действующая на отдельный заряд,движущийся в магнитном поле F_Л=q Bsinα. Направление силы Лоренца находится по правилу левой руки. Движение заряженных частиц в магнитном поле: Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол a между векторами v и В равен 0. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центро­стремительное ускорение. Отсюда следует, что частица будет двигаться по окружности. Если скорость v заряженной частицы направлена под углом  к вектору В , то ее движение можно представить в виде суперпозиции: 1) равномерного прямолиней­ного движения вдоль поля со скоростью v_||=vcos ; 2) равномерного движения со скоростью v_=vsin по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (в данном случае надо заменить v на v_=vsin). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю h= _II*T винтовая линия. Движение заряженных частиц в электрическом поле: Если частица, обладающая зарядом е, движется в пространстве, где имеется электрическое поле с напряжённостью E , то на неё действует сила eE. Напряженность Е-физическая величина, равная соотношению силы F, с которой электрическое поле действует на пробный точечный заряд q , к значению этого заряда. E=F/q.

Вопрос 2.5 Работа магнитного поля при движении проводника с током. При перемещении проводника с током совершается работа dА равная YdФ, где dФ-это магнитный поток, пересекаемый проводником при движении (или поток через площадь) А=JΔФ. Если в магнитном поле находится замкнутый контур, то работа равна произведению силы тока на изменение магнитного потока. Эта работа совершается не за счет энергии магнитного тока, а за счет источника тока А=Y(Ф₂-Ф₁). Магнитный поток численно равен числу линий магнитной индукции, пронизывающей поверхность S : ΔФ=ВΔScosα (Вб=1 Тл*м²) Если Ф>0 то α-0-90, если Ф<0 то cosα<0. В природе нет магнитных зарядов, поэтому линии магнитной индукции замкнуты. Индуктивность контура: магнитный поток, пронизывающий контур прямопропорционален силе тока Ф=L*Y, L-индуктивность контура(коэффициент пропорциональности)-Вб/A=Гн(генри). Индуктивность соленоида: L=Ф/Y=μμ₀n²V, индуктивность зависит от формы, размеров и среды.

Вопрос 2.6 Электромагнитная индукция. ЭДС индукции. В замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток индукционным. Явление электромагнитной индукции свидетельствует о том, что при изменениях магнитного потока в контуре возникает электродвижущая сила индукции. Было открыто в 1831г. Фарадеем. Ф=ВS По мере движения магнита к проводнику с потоком в нём начинает течь ток. Индукционный ток возникает при изменении магнитного потока, пронизывающего контур. Причём индукционный ток не зависит от причины изменения магнитного потока. ЭДС индукции возникает и в незамкнутом проводнике при его движении в магнитном поле. Рисунок. Направление индукционного тока определяется по правилу Ленца: индукционный ток всегда направлен так, чтобы противодействовать причине его вызывающей увеличения магнитного потока. Рисунок. ЭДС (ε) - отношение работы сторонних сил по разделению зарядов к величине этого заряда, иначе, способность данного источника давать необходимое количество зарядов необходимой энергии. Явление самоиндукции – это возникновение ЭДС индукции в контуре в результате изменения тока в самом этом контуре. Ф~J Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру. Магнитный поток, пронизывающий контур прямопропорционален силе тока. Ф=L*J (L-индуктивность контура). Основной закон электромагнитной индукции гласит, что индукционный ток возникает в проводящем контуре при всяком изменении магнитного потока, пронизывающего поверхность, охваченную этим контуром.  ε= - ЭДС (ε) в замкнутом контуре численно равна и противоположна по знаку скорости изменению магнитного потока через поверхность контура. Основной закон электромагнитной индукции гласит, что индукционный ток возникает в проводящем контуре при всяком изменении магнитного потока, пронизывающего поверхность, охваченную этим контуром. Проводник с протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. 

Вопрос 2.8 Основные положения теории электромагнитного поля Максвела. Вектор   изменяется со временем, а площадь S контура и угол α остаются постоянными. Опытным путём было доказано, что э.д.с. индукции ei может возникать и в неподвижном проводящем контуре (проводнике), находящемся в переменном во времени магнитном поле. В этом случае на свободные заряды в проводнике сила Лоренца не действует () и для объяснения возникновения э.д.с. индукции ei Максвелл сформулировал следующее положение (постулат), которое называют первым положением теории Максвелла: переменное во времени магнитное поле порождает в окружающем пространстве вихревое электрическое поле. Таким образом, Максвелл ввел новый вид поля – вихревое электрическое поле.

В отличие от электростатического поля линии вихревого электрического поля являются замкнутыми, они связаны с направлением вектора  dB/dt правилом левого буравчика и лежат в плоскости, перпендикулярной к вектору  (рис.4.17,в). Силы этого поля являются сторонними силами, они совершают работу по разделению разноимённых зарядов. Уравнения показывают:

1. источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. то магнитные поля могут возбуждаться либо движущими­ся зарядами (электрическими токами), либо переменными электрическими полями.

3. Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.

3.1. механические колебания .Смещение , амплитуды ,период, частота, фаза, и циклическая частота колебания .гармонические колебания. уравнение гарм. колебаний .Скорость и ускорения движения при гарм.колеб.. Связь ускорения со смещением.

Колебанием –назыв. изменения положения тела (или сост.тела)обладающее той или иной степенью повторяемости во времени . Мех. Колебания –колебания маятников струн ,частей машин и механизмов ,зданий мостов и др.сооружений. Ψ(t)=Acos(ω₀t+φ₀)-смущение от положения равновесия в любой момент времени t.А-амплитуда –максем.смущение зависит только от внешнего воздействия. Т-период колебаний –миним.промежуток времени за которое система возвращается в начальное положение (т.е время за которое фаза изменяется на время 2П);Т=2П/ω₀ ; T=t/N;v-частота величина равная числу полных колебаний ,совершающихся за еденицу времени v-1/T, φ(t)= φ₀+ ω₀t)-фаза (φ_{0-нач.фаза)-} периодические колебания –назыв. Колебания если зн-я всех функциях величин ,хор-их колебательную систему и изменяющихся при ее колебаниях ,повторяются через равные промежутки времени. Циклическая частота- величина равная числу полных колебаний совершающихся на 2П еденицу времени. ω=2П/T*2ПV/ Гарм. Колебания –проход по диф-ур. + ω₀²Ψ=0; + ω₀²; Ψ=0 ; + ω₀² =0-мат. Маят;. + ω₀² =0; ;. + ω₀² =0- колиб. Контур . Скорость дв-я точки совершающей горм. Колеб. V= =-A ω₀sin(ω₀t+ , уск-е :а= =- Aω₀²cos(ω₀t+ ; a_max

3.2.Представление гармонических колебаний в виде вращающегося вектора .Сложение двух гармонических колебаний с одинаковыми частотам совершающихся в одном направлении .условия усиления и максимального усилия колебаний. Условия ослабления и наибольшего ослабления колебаний .

Метод вращения вектора амплитуды –представление горм. колебаний в виде вектора длинна которого равна амплитуде колебаний а направление образует с осью Х угол равный начальной фазе векторная диаграмма .Сложение двух горм. Колебаний с одинаковыми частотами ,совершаются в одном направлении Ψ1(t)=A1cos(ω0t+ᵠ01), Ψ2(t)=A2cos(ω0t+ᵠ02), Ψ(t)=Acos(ω0t+ᵠ0);A²= A²₁+ A²₂+2A₁A₂cos(ᵠ2-ᵠ1)-амплитуда результ. колебания зависит отА1, А2 и от разности фаз Δφ=φ02-φ01cos

Δφ= Δφ=2πn;A=A1+A2-max к усилию колебания

cos Δφ=-1; Δφ=(2П+1);А= -к уменьшению колебания  

3.3.квазиупругая сила .математический и физический маятник .циклическая частота гармонического осциллятора .энергия колебаний .

Квазиупругая сила –направленная к центру сила F,величина которой пропорциональна расстоянию от r от центра 0 до точки приложения силы: F=с r, где с- коэф.Является центральной силой

М атем маятник –материальная точка подвешенная на навесной нити и совершающая колебания в вертик. Плоскости под действием сил тяжести.Вращение отн т.0

Осн. зак. динамики вращательного движения М=Iα;М=[r*F];r=l;в пр-ю на ось 0: M=mglsinφ; I=mr²=ml²=›-mglsinφ=ml =0 –диф-ое у-е. Малые колебания математического маятника является примером изохорных колебаний ,т.е. колебания частоты и период которых не зависит от амплитуды .

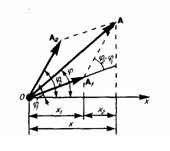
Ф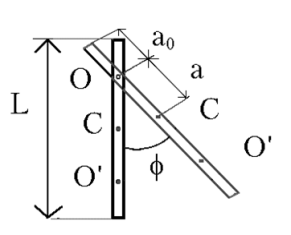 из. Маятник –твердое тело которое может вращаться под действием своей силы тяжести mg вокруг неподвижных гориз. оси 0 ,не проходя через цент тяжести тела –mglsinb=I ; φ=0

ω0= ; ω²₀ φ=0 –диф ур-ие горм. Колебаний . Lпр= – приведенная длинна –физ. Маятника –это длинна такого маятника периоды колебаний которого совпадают . Центр качания-точка в которой надо сосредоточить всю массу физ. Маятника ,чтобы его период колебаний не применялся (0₁)0-точка подвеса. Точка качания –точка расположения на продолжении отрезка прямой соединяющая точку подвеса и цент тяжести . гармонический осциллятор- мат. Точка массы m ,совершающая прямолинейные гармонические колебания под действием упругой силы ω= T=2П . Энергия колебаний – такая энергия сист. В любой момент времени равна сумме или энергии .В этот момент t или она равна мах пот-й энергии либо мах кинет-й энергии. W(t)=Wпот(t)+Wкин(t)=w^maxпот=w^maxкин.; Wпот(t)= , ω0= =›к= ω₀²m; Wпот(t)= = = ; Wкин(t)= = = ω₀²= ; A²

3.4.Упругие волны .Механизм и условия возникновения упругих волн .Поперечные и продольные упругие волны,условия их возникновения. Формулы скорости упругих волн в различных средах .Длинна волны.Циклическое волновое число .Ур-ие плоской волны .

Мех. упругая волна- волновым процессом или волной называется процесс распространения колибания в упр.среде и не связан с передачей энергии от источника колебания к частоте другой среды .При этом перенос массы в-ва не происходит, частицы среды испытывают лишь колебания относительно положений равновесия F=-kΨ. Вывод ур-я плоской бегущей волны Ψ(t)=Asinωt т.к. V распространения колебаний зависит от св-в упр-ой среды и она конечна, то частицы среды находится от источника на разном расстоянии придут в колеб.дв-е. не одновременно ,а со временем запаздывая r:τ= част. среды до которой дошло возмущение будет зависеть ΨN=Asinω(t-r)-смещение N частицы

(t-r)= (t- ) - =ωt- . Λ=VT-длинна волны к= -волновое число. ΨN=Asin(ωt-

kxN)-у-ие плоской бегущей волны. Ψ(x,t)-смещение относ.положения равновесия в один и тот же момент времени частиц среды наход. На разном расстоянии Х от источника. График бегущей волны частицы приходят в возмущение не одновременно ,а сдвигу по среде Ψ(x,t)=( ωt-кх)-среда бегущей волны зависит от t ,показывает что одно и то же состояние можно наблюдать на разных расстояниях от источника и в разные моменты времени.А-конст.для всех точек бегущей волны. Длинна волны - расстояние между частицей среды которые колеблются в среде (т.е.одно и тоже смещение )расстояние на которое волна распространяется за время равное периоду(время за которое частица совершает одно полное колебание ).Упр.волна назыв. Продольной –если частицы среды колеблются в направление распространения волны. Упругая волна назыв. Поперечной ,если частицы среды колеблются ,оставаясь в плоскостях перпендикулярных направлению распространения волны (тверд.тела).условия –передача энергии частицам упругой среды.

Формулы скорости волн в различных средах ,длина волны .циклическое волновое число .ур-е плоской волны. колебания частиц среды отн. равновесия могут происходить либо направлении распространения волны либо перпендикулярно (прод.попер.)зависит от св-в средыWпрод= Vпопер.= модуль сдвига среды, Е- модуль Юнга) Волновое число показывает сколько длин волн укладыв.на отрезке 2П единицу длинны.

3.5.Энергетические характеристики волн: объемная плотность энергии волны ,поток энергии волны ,плотность потока энергии волны, интенсивность волны, спектральная плотность потока энергии излучения .Уровень интенсивности ,уровень звукового давления ,уровень громкости звука.

Для хар-ки разр-я энергия волны пр-ве вводится –объемная плотная энергия волны W,которая показывает какая энергия волны была бы сосредоточена в ед. объема в данном месте ,если бы энергия волн была бы распределена в среде равномерно .

Wk=dWk/dV=1/2qA²ω² sin² (ωt-kx)-объем плотной кинет.энергии

Wп=dWп/dV=1/2qA²ω² sin² (ωt-kx)-- //- кинет.энергии

W=dW/dV=Wk+Wп=qA²ω² sin² (ωt-kx)-мгновенная объем плотной энергии

Wk=1/2qA²ω² –среды.знач.объема плотности энергии по времени

Поток энергии через поверхность- кол-во энергии переносимое волной через эту поверхность в ед. времени Фw=dW/dt .для характеристики распред.потока энергии вводится векторная велечина j плотн.потока энергии по мод.=потоку энергии через.ед площадку помещенную в данную данной точку1 перпед. Направленную в кот не переносится энергия.Напр совпад.с напр. Переноса энергии

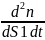= = , где α угол между нормалью к площадке и спор.волны-V, ds₁ =dScosα

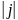=W*V , jвект.= W*Vвект. Для упругой волны –вектор Умова,для эл.магн.-Пойтинга

J=qvA² ω² sin² (ωt-kx)rjkt,.-dФw=jdScosα=jnds

Интенсивность –сред.по времени в данном месте Y= Jср=1/T =1/T =1/T*v =vWcp=1/2qA² ω²v

3.6. Электромагнитная волна – процесс распространения колебаний связанных между собой электрических и магнитных полей. ЭМ волны в отличии от других видов волн могут распространяться в вакууме. Возможность существования в вакууме ЭМ поля без источников, имеющего вид волн, со скорость света вытекает из уравнения Максвелла. Условием возникновения электромагнитных волн является ускоренное движение электрических зарядов. Так, изменение магнитного поля происхо­дит при изменении тока в проводнике, а изменение тока происходит при изменении скорости зарядов, т. е. при движении их с ускорением. Скорость рас­пространения электромагнитных волн в вакууме по расчетам Максвелла должна быть приблизительно равна 300 000 км/с.

Механизм возникновения электpомагнитной волны. Его суть заключена в связи соседних участков поля, вследствие котоpой состояние одного участка поля с запаздыванием пеpедается дpугому, соседнему. Электpомагнитное поле описывается "двумя полями": электpическим Е и магнитным В. Изменение во вpемени одного поля в окpестности данной точки, в котоpой оно pассматpивается, поpождает дpугое поле: изменение поля Е поpождает поле В и наобоpот. Пеpеменное во вpемени электpическое поле поpождает в соседних точках пеpеменное магнитное поле, в свою очеpедь пеpеменное магнитное поле в своей окpестности поpождает пеpеменное электpическое. Эти поpождения пpоисходят не мгновенно, а с опpеделенным запаздыванием, вследствие чего и создается электpомагнитная волна.

Скорость распространения волн:

Скорость электромагнитных волн в вакууме (ε = μ = 1)

Длина волны λ в синусоидальной волне связана со скоростью υ распространения волны соотношением λ = υT = υ / f, где f – частота колебаний электромагнитного поля, T = 1 / f.

Показатель преломления вещества – величина, равная отношению фазовых скоростей света в вакууме и в данной среде

3.7. Интерференция – явление наложения волн с образованием устойчивой картины максимумов и минимумов. Интерферировать могут только когерентные волны.

Когерентные волны – волны, приходящие в данную точку пространства с постоянной во времени разностью фаз. Необходимым условием когерентности является равенство частот.

1 Случай (max):

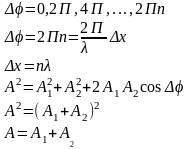
Разность хода равна целому числу длин волн.

2 Случай (min):

Разность хода равна нечетному числу длин полуволн.

При интерференции немонохроматического света имеет место разложение этого света на составляющие его цвета. Интерференционные полосы имеют такой же вид, как и при монохроматическом свете, но интерференционная картина при белом свете будет представлять собой чередующиеся цветные полосы соответствующей формы – повторяющиеся спектры. Расстояние между соседними max или min для данной волны называется шириной интерференционной полосы:

3.8. Интерференция света в тонких пленках.

Пусть на плоскопараллельную прозрачную пленку с показателем преломления п и толщиной d под углом i (рис. 249) падает плоская монохроматическая волна (для простоты рассмотрим один луч). На поверхности пленки в точке О луч разделится на два: частично отразится от верхней поверхности пленки, а частично преломится. Преломленный луч, дойдя до точки С, частично преломится в воздух (п₀=1), а частич­но отразится и пойдет к точке В. Здесь он опять частично отразится (этот ход луча в дальнейшем из-за малой интенсивности не рассматриваем) и преломится, выходя в воздух под углом i. Вышедшие из пленки лучи 1 и 2 когерентны, если оптическая разность их хода мала по сравнению с длиной когерентности падающей волны. Если на их пути поставить собирающую линзу, то они сойдутся в одной из точек Р фокальной плоскости линзы. В результате возникает интерференционная картина, которая опреде­ляется оптической разностью хода между интерферирующими лучами.

О птическая разность хода, возникающая между двумя интерферирующими лучами от точки О до плоскости АВ,

где показатель преломления окружающей пленку среды принят равным 1, а член ± ₀/2 обусловлен потерей полуволны при отражении света от границы раздела. Если п>n₀, то потеря полуволны произойдет в точке О и вышеупомянутый член будет иметь знак минус; если же п<n₀, то потеря полуволны произойдет в точке С и ₀/2 будет иметь знак плюс. Согласно рис. 249, OC=CB=d/cosr, OA = OB sin i = 2d tg r sin i. Учитывая для данного случая закон преломления sin i = n sin r, получим

С учетом потери полуволны для оптической разности хода получим

(174.1)

Для случая, изображенного на рис. 249 (п>n₀),

В точке Р будет интерференционный максимум, если (см. (172.2))

(174.2)

и минимум, если (см. (172.3))

(174.3)

Интерференция, как известно, наблюдается, только если удвоенная толщина пластинки меньше длины когерентности падающей волны.

1. Полосы равного наклона (интерференция от плоскопараллельной пластинки). Из выражений (174.2) и (174.3) следует, что интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами ₀, d, п и i. Для данных ₀, d, и n каждому наклону i лучей соответствует своя интерференционная полоса. Ин­терференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона.

Лучи 1' и 1", отразившиеся от верхней и нижней граней пластинки (рис. 250), параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, ин­терферирующие лучи 1' и 1" «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения исполь­зуют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы (на рис. 250 ее оптическая ось параллельна лучам 1' и 1"), в эту же точку придут и другие лучи (на рис. 250 – луч 2), параллельные лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы. Легко показать, что если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона будут иметь вид концентрических колец с цент­ром в фокусе линзы.

2. Полосы равной толщины (интерференция от пластинки переменной толщины). Пусть на клин (угол  между боковыми гранями мал) падает плоская волна, направле­ние распространения которой совпадает с параллельными лучами 1 и 2 (рис. 251). Из всех лучей, на которые разделяется падающий луч 1, рассмотрим лучи 1' и 1", отразившиеся от верхней и нижней поверхностей клина. При определенном взаимном положении клина и линзы лучи 1' и 1" пересекутся в некоторой точке А, являющейся изображением точки В. Так как лучи 1' и 1" когерентны, они будут интерферировать. Если источник расположен довольно далеко от поверхности клина и угол  ничтожно мал, то оптическая разность хода между интерферирующими лучами 1' и 1" может быть с достаточной степенью точности вычислена по формуле (174.1), где d — тол­щина клина в месте падения на него луча. Лучи 2' и 2", образовавшиеся при делении луча 2, падающего в другую точку клина, собираются линзой в точке А'. Оптическая разность хода уже определяется толщиной d'. Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину (в общем случае толщина пластинки может изменяться произвольно). Интерференционные полосы, возникающие в резуль­тате интерференции от мест одинаковой толщины, называются полосами равной толщины.

Так как верхняя и нижняя грани клина не параллельны между собой, то лучи 1' и 1" (2' и 2") пересекаются вблизи пластинки, в изображенном на рис. 251 случае — над ней (при другой конфигурации клина они могут пересекаться и под пластинкой). Таким образом, полосы равной толщины локализованы вблизи поверхности клина. Если свет падает на пластинку нормально, то полосы равной толщины локализуются на верхней поверхности клина.

3.9

Простейший случай интерференции при наложении падающей и отраженной волны. Эти волны когерентны и создают в каждой точке пространства колебания вдоль одной прямой. Наложение таких волн приводит к образованию стоячей волны.

S ₁=A₀*sin(ωt-kx) – уравнение падающей

S₂= A₀*sin(ωt+kx) – уравнение отраженной

S=S₁+S₂= A₀*sin(ωt-kx)+ A₀*sin(ωt+kx)

S=2A₀coskxsinωt – уравнение стоячей волны

A=2A₀|coskx|

|coskx| - амплитуда стоячей волны

A₀ – амплитуда падающей/отраженной

Коорд. Узлов: А=2A₀|coskx|=0

|coskx|=0; kx=±(2N+1)π/2

=±(2N+1) => X_узл.=±(2N+1)

Расстояние между соседними узлами: X_N+1 – X_N =λ/2

Координаты пучности: A=2A₀|coskx|=2A₀; |coskx|=1; kx=±Nπ; X_пучн=±Nλ/2

Расстояние между соседними пучностями: X_N+1-X_N=λ/2; ∆X=λ/2

Фаза колебаний по разные стороны узла отличается на π.

Точки, лежащие по разные стороны узла колебаний в противофазе.

Все точки между двумя соседними узлами колеблется синфазно.

Объемная плотность кинетической и потенциальной энергии:

ω_k= =2pA²ω²cos²kxsin²ωt; при coskx=0 – узлы энер., при coskx=1 – пучн. энер.

ω _П=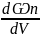 =2pA²ω²sin²kxsin²ωt; при sinkx=0 – узлы энер., при sinkx=1 – узлы энер.

- график распределения амплитуд объемной плотности энергии.

ω_ka=2pA²ω²cos²kx

ω_па=2pA²ω²sin²kx

Max-мы, потенциальная и кинетическая энергия разобщены на T/4 и λ/4

О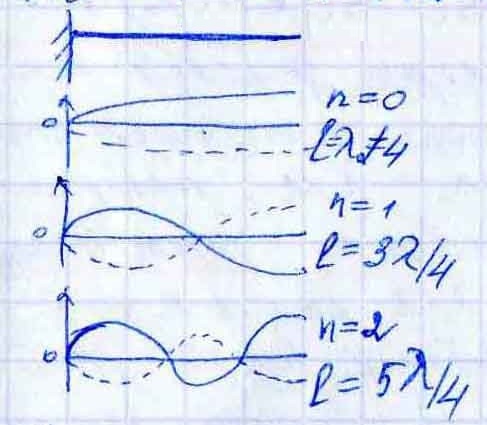 граниченные среды (отрезок стержня с закрепленными или свободными концами, струна, пластина) представляют собой колебательные системы. Собственные колебания от таких систем связаны с образование стоячих волн в них, форма которых зависит от условия отражения на границах среды. Возбудить систему можно кратковременным воздействием на какую-либо ее часть(удар, щипок). Образуется волновой импульс. Так как стоячие волны существуют сами по себе(в отсутствии внешних сил), то связанные с ними колебания ограниченной системы – собственные(затухающие). Собственные колебания стержня укреп. с одного конца (если ударом возбудить продольные и поперечные волны, то в нем установятся стоячие волны) на закрепленном конце – узел, на свободном – пучность.

На длине стержня уклад. нечетное число λ/4, т.е.

l= (2n+1) λ_n/4; n=0,1,2

λ_n= ; γ_n= = ;

-скорость распространения упругой волны в стержне

при n=0; γ₀= /4l – основная волна все последующие обертоны; γ_n= γ₀(2n+1)

Стержень укрепленный с двух сторон:

l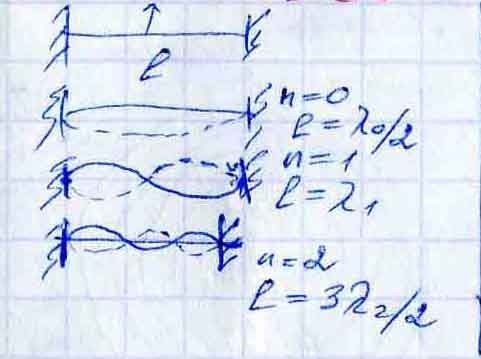 =n*λ_n/2; λ_n=l/n; γ_n = *n

резонанс – резкое увеличение амплитуды при совпадении частот.

Волной называют колебания, распростра­няющиеся в пространстве с течением времени. Важнейшей ха­рактеристикой волны является ее скорость. Волны любой природы не распространяются в пространстве мгновенно. Электромагнитная волна - процесс распространения электромагнитного поля в пространстве. Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля. Условия возникновения – наличие взаимодействия между частицами среды. Если центр колебаний точечный, то колебания распространяются по окружности.

3.10

Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятст­вий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Например, звук хорошо слышен за углом дома, т. е. звуковая волна его огибает.

Явление дифракции объясняется с помощью принципа Гюйгенса (см. § 170), соглас­но которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.

Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 256). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента време­ни, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия.

Согласно принципу Гюйгенса — Френеля, световая волна, возбуждаемая каким-ли­бо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверх­ностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех коге­рентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии — такая же, как при отсутствии экрана.

Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света.

Д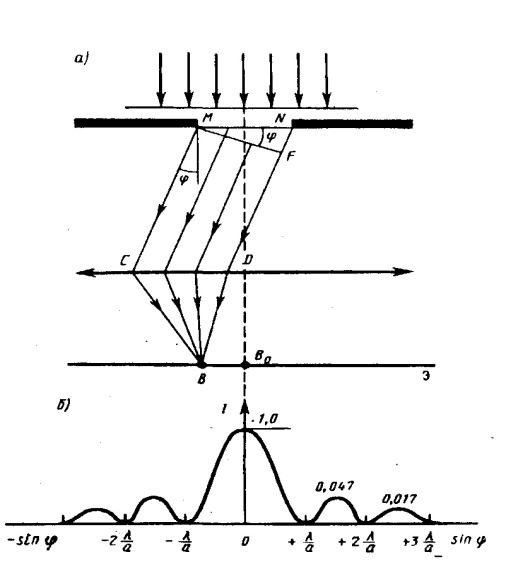 ифракция Фраунгофера(дифракция в параллельных лучах), имеющая боль­шое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис.а). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении ,

где F — основание перпендикуляра, опущенного из точки М на луч ND.

Число зон Френеля, укладывающихся на ширине щели, зависит от угла . От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то

и в точке В наблюдается дифракционный минимум (полная темнота).

если же число зон Френеля нечетное, то

и наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в направлении =0 щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интен­сивностью, т. е. в точке В₀ наблюдается центральный дифракционный максимум.

Дифракция Фраунгофера на дифракционной решетке.

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей рав­ной ширины, лежащих в одной плоскости и разделенных равными по ширине непроз­рачными промежутками.

Дифракционная картина на решетке определяется как результат взаимной ин­терференции волн, идущих от всех щелей, т. е. в дифракционной решетке осуществля­ется многолучевая интерференция когерентных дифрагированных пучков света, иду­щих от всех щелей.

Р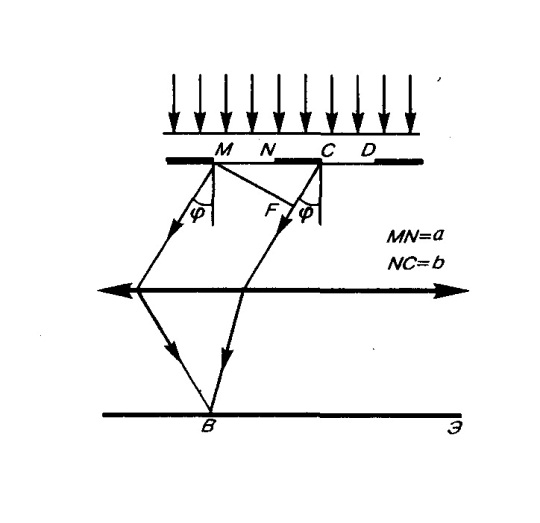 ассмотрим дифракционную решетку. На рис. для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна а, а ширина непрозрачных участков между щелями b, то величина d=a+b называется постоянной (периодом) дифракционной решетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления  одинаковы в пределах всей дифракционной решетки:

-условие главных минимумов

-условие дополнительных минимумов

- условие главных максимумов

4.1 Тепловое излучение, его энергетические характеристики. Законы Киргофа, Стефана-Больцмана, Вина. Постулаты Планка.

Тепловое излучение – электромагнитное излучение испускаемое телом за счет его внутренней энергии. С увеличением температуры: 1)интенсивность увеличивается 2)меняется спектральный состав – max смещается в область меньших длин волн. Тепловое излучение – единственное излучение которое находится в равновесии с источником.

Характеристики ТИ: 1) Поток энергии Ф=dw/dt (Вт) dw – энергия теплового излучения всех длин волн испускаемых за время dt.

2) Энергетическая светимость M = dФ/dS = dw/dS*dt. Численно равна энергии испускаемой единицей площади за ед времени М=w/S*t. М – характеризует интенсивность излучения при данной температуре

3) Спектральная плотность энергетической светимости. Численно равна энергии электромагнитных волн с длинами волн до испускаемых с ед площади за ед времени и отнесенных к ширине интервала .

4) Коэффициент поглощения 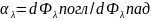Показывает какая часть энергии подающего данной длины волны поглощается.

1)Закон Киргофа. Физ смысл: чем больше тело излучает тем больше поглощает. Отношение спектра плотности энергетической светимости тела к его коэф. поглощения одинаково для всех тел и равно спектральной плотности энергетической светимости абсол черн тела при данной температуре. .

2)Закон Стефана-Больцмана Энергетическая светимость прямо пропорциональна температуре в 4 степени.

3) Закон смещения Вина м*К Длина волны соответсвует max значению спектральной плотности энергетической светимости абс черн тела обратно пропорциональна его температуре.

4.2 Фотоэлектрический эффект . Вольтамперная характеристика фототока. Опытные закономерности фотоэффекта. Уравнение Эйнштейна для фотоэффекта.

Фотоэффект – вырывание электронов из в-ва под действием падающего на него света.

1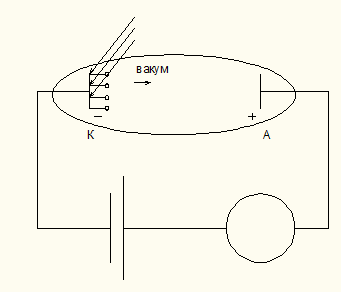 )Даже при U=0, ток будет существовать. 2) n – число электронов выбиваемых с катода 3) Задерживающее напряжение

1 закон Ток насыщения прямопропорционален световому потоку падающему на катод.

2 закон Max скорость вылетающих электронов не зависит от интенсивности падающего света а зависит только от частоты

3 закон Для каждого в-ва существует такая длина волны (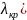 что для всех волн больше чем 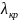ток отсутствует .

Формула Эйнштейна для фотоэффекта Энергия поглощенного кванта – расходуется электроном на совершение работы выхода и на кинетическую энергию электрона

4.3 Фатоны. Корускулярно-волновая природа света.

Фатон – элементарная микрочастица которая является мельчайшей порцией эл магнитного излучения. 1)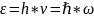

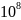2)Закон Эйншт. О связи массы с энергией 3) c=3* м/c 4) Фатон обладает импульсом

Корпускулярно-волновая природа

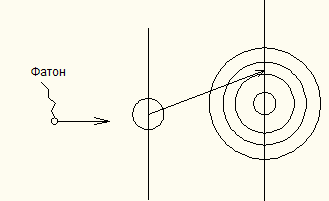Фатон попадает в какую то точку экрана. При пропускании N количества фатонов мы так же увидим полосы как и при дифракции. Вероятность попадания фатона в определенную точку 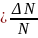где дельта N –скок попало в точку, а N скок всего фатонов. Квадрат амплетуды волны в данной точке определяет вероятность попадания фатонов в эту точку.

Свет – поток фатонов. Носителями энергии импульса массы являются фатоны. Распределение фатонов в пространстве имеет вероятностный характер и вероятность определяется амплетудой волны.

4.4 Ядерная модель атома. Результаты квантово-механического рассмотрения поведения электрона в водородноподобном атоме. Излучение и поглощение энергии атомами и молекулами

В 1991 г Резерфорд проводя опыты по рассеиванию альфа частиц предложил модель. Диаметр ядра м диаметр атома м. Ядерная модель противоречит классич физике. Двигаясь с ускорением электрон должен излучать магнитные волны – энергия уменьшается, следовательно должен упасть на ядро. Постулаты Бора:

1. Существует стационарное состояние находясь в котором атом не излучает.

2. Стационарные орбиты должны удовлетворять следующему условию

3. При переходе электроне из 1 стационарного состояния с энергией в другое излучает или поглащает 1 фатон и энергия его - постоянная планка на частоту равно разнице энергий

Атом переходит в возбужденное состояние при сообщении энергии, при взаимодействии с фаноном, при сталкновении с другим атомом. При излучении и поглащении фотона возможны лишь такие переходы при которых выполняются правила отбора. Связаны с законом сохранения момента импульса

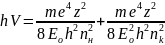
Спектр атома водорода имеет линейчатый характер . R= 3.3* - постоянная ридберга.

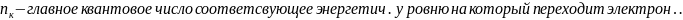
Результаты квантово- механического рассмотрения …

где h- постоянная планка n =1,2,3… - главное квантовое число, характеризует уровень на котором находится электрон.

Электрон в атоме характеризуется орбитальным моментом импульса. -2ое квантовое число.

Направление момента импульса может быть только таким, что его проекция равна -магнитное квантовое число. Оно определяет допустимые значения момента импульса.

СПИН – собственный момент импульса. S=0;1/2;1;3/2. Проекция СПИНА по заданному направлению 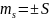– 4ое квантовое число. Характеризует величину и направление СПИНА.

4.5 Состав ядер атомов. Радиоактивность ядер. Реакции деления и синтеза ядер.

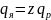
Заряд ядраопределяется числом протонов ядре. z-зарядовое число определяет порядковый номер в таблице Менделеева. 1а.е.м. = 1/27 массы изотопа углерода.

Общее число протонов и нейтронов это массовое число. А=z+N (z – число протонов N – число нейтронов) – нуклоны Масса ядра практически совподает с массой атома. Плотность ядра: .

Радоактивность – самопроизвольное превращение неустойчивых ядер одного химического элемента в ядра другого элемента. Такое превращение может происходить путем самопроизвольного распада ядер , протонная радиоактивность и спонтанное деление тяжелых ядер. При из ядра вылетают альфа частицы. Масса нейтрона больше суммы масс протона и электрона. Поэтому возможен самопроизвольный распад нейтрона на протон и электрон. При этом образуется еще одна частица не имеющая ни массы ни заряда – антинейтрино е превращение атома ядра в результате которого его заряд увеличивается или уменьшается на один элементарный элек заряд называется .

Ядерные свойства : 1)Короткодействие, 2)зарядовая независимость,3) не центральные, 4)свойство насыщения ( каждый нуклон взаимодействует лишь с соседями). Энергия связи – энергия на расщепление нуклона. -деффект масс.

А=z+N

Синтез –взаимодействие двух ядер может образовать новое ядро. Превращение ядер становится возможным только, когда они так близко подходят друг к другу что в действии вступают ядерные силы. Для того чтобы 2 ядра могли преодолев силы кулоновского отталкивания приблизится друг к другу они должны иметь достаточно высокие кинетические энергии. Таким образом ядра могут взаимодействовать когда вещество имеет температуру порядка 10⁷-10⁸К, поэтому процесс слияния называется реакцией термоядерного синтеза. Реакция термоядерного синтеза является экзотермической и может быть использована для получения тепловой энергии.

4.7 Молекулярно-кинетические представления о строение в-ва в различных агрегатных состояниях. Статистический метод описания состояния и поведения систем многих частиц. Функция распределения частиц по состояниям.

1) Все молекулы хаотически движутся . 2) Все тела состоят из молекул 3) Взаимодействие между молекулами.

Рисунок к 3ему пункту

В ыделяют 3основных агрегатных состояний твердое, жидкое, газ. Изменение агрегатного состояния это термодинамические процессы, называемые фазовыми переходами. Твердое в жидкое – плавление, жидкое в газообразное – испарение и кипение, твердое в газообразное – сублимация, газообразное в жидкое или твердое – конденсация, жидкое в твердое – кристаллизация. 1)Твердое состояние характеризуется способностью сохранять объем и форму. Атомы тела совершают лишь небольшие колебания вокруг состояния равновесия.2)Жидкое состояние, при котором в-во обладает малой сжимаеиостью, хорошо сохраняют объем, однако не особо сохраняют форму. 3)Газ состояние, характеризующееся хорошей сжимаемостью, отсутствием способности сохранять объем и форму. Атомы и молекулы гааз ведут себя относительно свободно, расстояние между ними гораздо больше их размеров.

При КТ (кинетической энергии) –в-во находится в газообразном состоянии.

КТ= - жидкое состояние

КТ – твердое

Существует 3 метода описания частиц: 1) динамический ( не подходит для веществ с большим числом частиц) 2) Статистический ( основан на теории вероятности), 3)термодинамический ( основан на законах термодинамики)

Для статистического метода где .

Распределение Максвела.

Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.

Ф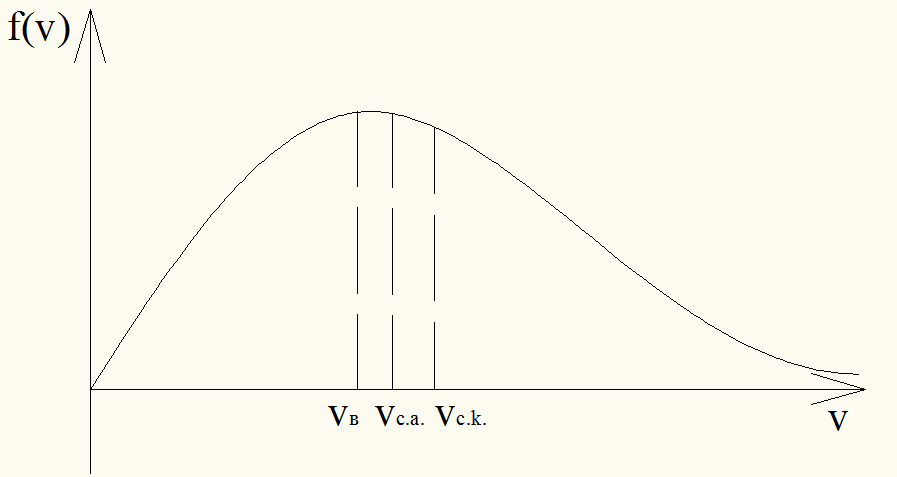 ормула наибольшей вероятности Vв

Среднеарифметической вероятности Vс.а. =

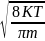
Среднеквадратичной вероятности Vc.k. =

При изменении температуры газа будут изменяться скорости движения всех молекул, а, следовательно, и наиболее вероятная скорость. Поэтому максимум кривой будет смещаться вправо при повышении температуры и влево при понижении температуры. Высота максимума не будет оставаться постоянной.