У словия прочности и жесткости при кручении

I II

r

N¹ C¹ δ

O O¹

φ M_вр

K γ N C

L

Угол сдвига для элемента, лежащего на поверхности стержня, равен отношению отрезка NN¹ к длине элемента dz

(1)

Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса δ и повторяя те же рассуждения, получим угол сдвига для элемента, отстоящего на расстоянии δ от оси стержня

(2)

На основании закона Гука при сдвиге имеем

(3)

Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.

Эпюра касательных напряжений

τ _max

D

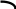D¹

φ r δ τ

C¹ C

B¹ B

В центре тяжести касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точках сечения, расположенных у поверхности сечения.

Равнодействующий момент касательных напряжений в сечении:

(4)

где -элементарный крутящий момент внутренних сил, действующих по площадке dA.

Подставив в (4) значение напряжений из формулы (3), получим

(5)

Имея в виду, что

, (6)

Где - полярный момент инерции сечения, получим

(7)

Подставляя значение в формулу (3), имеем

(8)

В частном случае, когда на стержень действует один внешний скручивающий момент М, из условия равновесия отсеченной части стержня получим М_К=М.

Таким образом, окончательная формула для определения касательных напряжений при кручении имеет вид

(9)

Эта формула показывает, что, в точках, одинаково удаленных от центра сечения, напряжения τ одинаковы. Наибольшие напряжения в точках у контура сечения равных

, (10)

Где

(11)

Геометрическая характеристика W_P называется полярным моментом сопротивления или моментом сопротивления при кручении.

Для круглого сплошного сечения .

Для кольцевого сечения

Где

Условие статической прочности вала при кручении имеет вид

Задачи на условия прочности при кручении:

1. Проверка прочности

2. Проектный расчет круглого сплошного сечения ; ; .

Кольцевого сечения ;

3. Определение максимально допустимой нагрузки

Условия жесткости при кручении

откуда

, но , тогда

φ₀ – угол закручивания, приходящийся на единицу длины [м]

Задачи на условия жесткости при кручении:

1. Проверка жесткости

2. Проектный расчет для круглого сплошного сечения ,

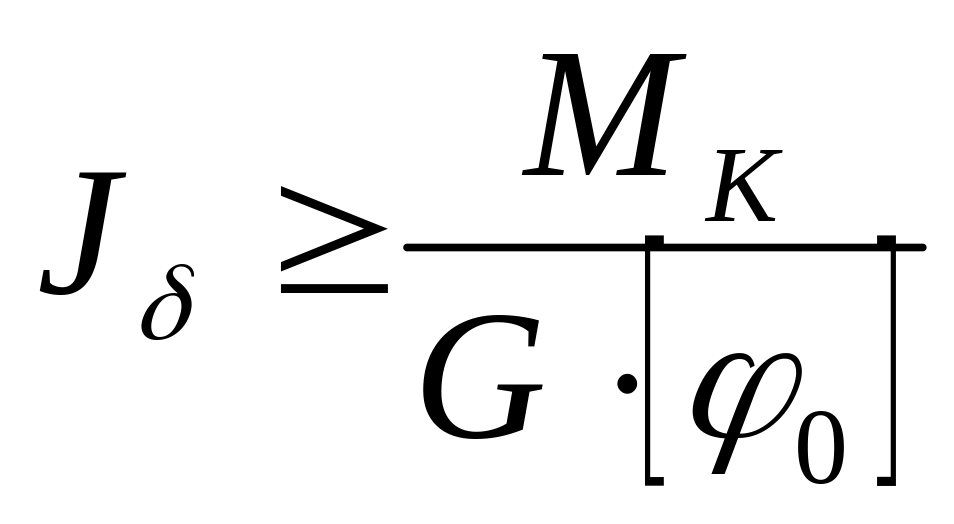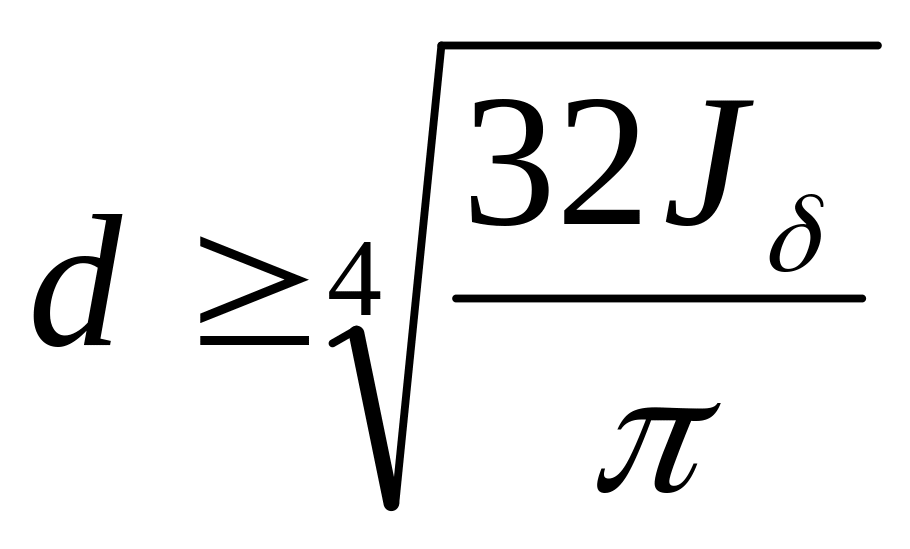
Для кольцевого сечения ;

Зависимость крутящего момента и мощности на валу

3. Определение допускаемой нагрузки

ПРИМЕРЫ РЕШЕНИЯ РАСЧЕТНО-ГРАФИЧЕСКИХ ЗАДАЧ ПО ТЕМЕ

КРУЧЕНИЕ

Задача1

Для стального вала требуется:

1. Определить величины моментов, подводимых к шкиву 1 и снимаемых со шкивов 2,3,4.

2. Построить эпюру крутящих моментов на валу.

3. Определить предельный диаметр вала из расчета на прочность и жесткость, если Р₂=50кВт

Р₃=40кВт

Р₄=30кВт

n =170 об/мин

[τ]=20МПа

[φ₀]=0,25 град/м

Окончательно принимаемое значение диаметра вала должно быть округлено до ближайшего большего четного, или оканчивающегося на 5 числа (мм).

IV M₂ III M₁ II M₃ I M₄

0 2,81кНм -3,93кНм -1,68кНм 0

Определяем мощность, подаваемую на вал

Р₁=Р₂+Р₃+Р₄=50+40+30=120 (кВт)

Вращающие моменты на шкивах

;

;

По найденым вращающим моментам строим епюру крутячих моментов.

М_Кр1= -М₄ = -1,68(кНм)

М_Кр2 = -М₄-М₃ = -1,68-2,25 = -3,93(кНм)

М_Кр3=-М₄ -М₃+М₁=-3,93+6,74=2,81(кНм)

М_Кр4=-М₄ -М₃+М₁-М₂=2,81-2,81=0

Из эпюры выбираем M_max по модулю M_max=M_Kp2=3,93(кНм)

Определяем минимальны размер вала по условию прочности

Определяем диаметр вала по условию жесткости

Принимаем d=104мм

Задача 2

В поперечном сечении полого вала возникает крутящий момент М_К=6000Нм. с=d/D=0,8. [τ]=50МПа.

Найти диаметр вала по условию прочности и экономию веса по сравнению со сплошным валом в тех же условиях.

Решение

;

где

ИЗГИБ

Прямым чистым изгибом называется вид деформации, при котором в поперечных сечениях стержней возникает один внутренний силовой фактор -изгибающий момент.

Прямым поперечным изгибом называется вид деформации при котором в поперечных сечениях возникают два внутренних силовых фактора: поперечная сила и изгибающий момент.

Стержни, работающие на изгиб, называются балками.

Эпюры поперечных сил- диаграммы изменения поперечных сил по длине балки.

Эпюры изгибающих моментов- диаграммы изменения изгибающих моментов по длине балки.

Поперечная сила в сечении численно равна алгебраической сумме проекций на вертикальную ось всех внешних сил, действующих по одну сторону от рассматриваемого сечения.