The rule of phases and its employment

1. Main notions and definitions

The system. Physico-chemical system is a part of substance, chosen and removed in such way, that one can observe changes and finite conditions depending on defining terms in it. A phase is a part of a system, possessing identical chemical thermodynamic, physical properties. Neigbouring phases form boundary surface with each other.

Components. The components are chemically individual components of the system of less amount, that are sufficient to form any phase of equilibrium system.

Freedom degrees. Freedom degrees are independent thermodynamic parameters of phases of the system, which is in stable equilibrium, able to take arbitrary values in that interval, at which the number of phases doesn’t change.

The number of freedom degrees. The number of freedom degrees is the least number of independent parameters, necessary to define the system condition. The number of phases, number of components and number of freedom degrees are connected between each other by Gibb’s equation.

F + p = k + 2

where, F – number of freedom degree, p – number of phases, k – number of components.

In many cases silicate systems are condensed, and pressure has little influence on properties of such systems. Paying no regard to pressure, one can write in such cases

F + p = k + 1

While research equilibrium systems Clausius-Klapeiron equation has great significance, which describes volume change at phase transformations with temperature and critical heat.

Mathematically this dependence is expressed by equation:

where Q – heat of phase transformation; V₁ – specific volume of low temperature phase; V₂ – specific volume of high temperature phase; T – absolute temperature of phases equilibrium.

The equation (I,3) shows that if difference of specific volumes V₂ – V₁ is positive, that is at heating the volume increases, at presence of equation of positive quantity in the right part: temperature and latent heat of phase transformation (heat is evolved), the left part of equation will be positive.

Using equation (I,3) one can define the direction of the change of equilibrium pressure P depending on the change of equilibrium temperature and change quantity P on 1° temperature. This method of definition is suitable for any phases transformation, if only difference of phases volumes V₂ – V₁ and heat of this transformation are measurable.

For two-component systems the rule of phases takes the form

F + p = k + 2 = 2 + 2 = 4

At excluding vapour phase, and therefore pressure as changeable one, we get

F+ p = 2 + 1 = 3

At nonvariant condition of equilibrium system, when F = 0, maximum number of phases will be

p_max = 3

when the number of phases is minimal p = 1, maximum possibly number of freedom degrees

F_max = k + 1 – 1 = 2

Temperature and concentration of one of the components are independent parameters in such a system. The concentration of another component is defined by difference from 100 and is a dependent parameter.

The dependence between chemical, phase composition, temperature and concentration (in some cases pressure as well) is expressed by graphic diagrams of condition. Using them, one can define kind and number of phases, their composition and number of each in equilibrium condition at the given parameters and mixture compositions, and also changes of these characteristics when heated and cooled. At this the given changes must be considered as continuous chain from separate equilibriums.

At constant pressure the rule of phases for two-component systems gives the following correlations of phases numbers and freedom degrees:

Number of phases	Number of freedom degrees	Condition of systems	Geometric element of the diagram
1	2	Divariant	Field of stability
2	1	Monovariant	Boundary curve
3	0	Nonvariant	Nonvariant point

Example. Densities of liquid and solid tin at melting temperature (231,9°C) under pressure 1_atm correspondingly equal to 6,988 and 7,184 g/cm³. Melting heat of tin – 1690 cal/mole.

To define melting temperature of tin under pressure 100_atm.

Solution. We define the change of the temperature at increasing of pressure for 1_atm that is the quantity of , which is calculated from Clausius-Klapeiron (I,3)

where T – absolute melting temperature under the pressure 1_atm; (V₂ – V₁) – difference of volumes (specific) of liquid and solid tin, cm³/g; Q – specific melting heat of tin, cal/mole,

where 41,3 – l-atm^*; 118,7 – molecular weight of tin.

After we get

* 1 cal = 4,18·10³J = 41,3 l·atm

Melting temperature under the pressure – 100_atm

t = 231,9 + 3,35·10^-3 · 99 = 232,23⁰ C

Control issues

№ 1

1. Give a definition «System, components, freedom degrees, number of freedom degrees».

2. The rule of phases of Gibbs.

3. The diagrams of the state of one-component systems. What is enantiotropic and monotropic transformations?

Assignments for student’s self-directed studies (SSDS) 1

1. Characteristics and methods of receiving colloid systems.

2. One-component systems SiO₂, Al₂O₃, MgO, ZrO₂.

Practical training № 2. Decision of practical tasks on twocomponent diagrams of condition. Definition of phase structure and quantitave contents of phases in silicate systems and other refractory materials.

Two-component systems

Phase transformations in two-component systems consist not only in melting processes and crystallization or polymorphic transformations; at this also intersolution of components in liquid and solid phases, formation of chemical compounds and etc. occur.

The phase correlations in two-component systems are obviously represented as corresponding state diagrams.

Since the influence of pressure is usually not taken into account in silicate systems, melted at very high temperatures, as variables, defining this or that state of the system, in coordinate axes the temperature and concentration of one of the components are put aside. It is it designated through x, the concentration of the second component in the studied composition can always be defined by the expression y=(100-х), and the state diagram of the system is thus brought to two dimensional graphics.

State diagrams allow to define the way of crystallization and the way of melting for any composition in the given system. The conditional term “the way of crystallization” is the consequences of phase changes and changes of compositions of liquid and solid phases at cooling of fusion of the given composition, described in the diagram; “the way of melting” is the same consequence, but for solid mixture, subjected to heating up to full fusion. For one and the same composition the way of crystallization and the way of melting are graphically identical, but opposite in the direction and consequence of phase transformations.

Two-component systems are divided into the following types: systems with eutectic melting; with chemical compound, melted with decomposition; with chemical compound, decomposed in solid form; polymorphic transformations of one or more crystalline phases; with liquation; systems with solid solutions of unlimited or limited miscibility – with eutectic or peritectic points.

Three-component systems

In methodical instructions for practical classes a brief abstract of the theory, necessary for calculations, equation and formula is given, with following examples with solutions and tasks. Examples and tasks express the issues of the theory and practice of the technology of silicates and oxides.

Three-component systems

Equilibrium phase composition of three-component depending on the temperature and concentrations is described in space diagrams.

As a foundation of this diagram equilateral concentration triangle is often chosen, in which concentrations of components are described in the same scale. Compositions of points of pure components – on the corresponding sides of the triangle, triple compositions – inside the triangle. All the points inside the triangle represent any correlations of three components, sides of the triangle are divided into 100 parts to count any concentration of mixtures.

Temperatures of full melting of mixtures are indicated by the points of vertexes of perpendiculars, erected on a certain scale to the concentration triangle in corresponding compositions of mixtures. The space diagram is limited by three plane two-component diagrams from sides, from the top – by space liquation, above of which only one-phase space of liquid is located.

To define the composition of the mixture of any point inside the triangle of the concentration it is necessary to draw two straight lines through the point, parallel to any two sides of the triangle. Then on the third side of the triangle three cuts will be chipped out, corresponding to the percentage content of components of the mixture in the given plotted point.

№ 2

1. What diagrams of the state of two-component systems do you know?

2. How are compositions of chemical compounds in diagrams of two-component systems described?

3. What is connoda?

Assignments for SSDS 2

1. Two-component systems, structure elements and rules of work with state diagrams.

2. Two-component system Na₂O – SiO₂ .

№3

1. How are chemical compounds, melted congruently and incongruently described in two-component systems?

2. What are polymorphic transformations?

3. How is the field of liquation designated in two-component diagrams of the state?

Assignments for SSDS 3

1. Main types of diagrams of the state of two-component systems and rules of work with them.

2. Two-component systems MgO –SiO₂

№ 4

1. What is geometric image of chemical compound in the diagram of the state of two-component systems designated by?

2. How is the way of crystallization in two-component systems defined?

3. What is liquation? Give examples.

Assignments for SSDS 4

1. Two-component system Al₂O₃ –SiO₂

2. Two-component system CaO –SiO₂.

№ 5

1. What kinds of three-component systems do you know?

2. How is phase composition of substances in three-component diagrams of the state defined?

3. How is quantative composition of substances in three-component diagrams of the state defined?

Assignments for SSDS 5

1. Three-component systems, elements of the structure of state diagrams.

2. Essence of experimental methods of construction of state diagrams.

№ 6

1. How are chemical compounds in three-component diagrams of the state described?

2. How is the way of crystallization in three-component systems defined?

3. How is the temperature of the beginning of crystallization and full melting of the material in three-component systems defined?

Assignments for SSDS 6

1. Static method of the construction of state diagrams.

2. Dynamic method of the construction of state diagrams.

№ 7

1. What elements of the structure of three-component systems do you know?

2. What is the field of liquation three-component systems?

3. What is the role of polymorphic transformations in three-component systems?

Assignments for SSDS 7

1. Three-component system K2O-Al₂O₃ –SiO₂

2. Three-component system Na₂O - CaO –SiO₂.

№ 8

1. What compounds are designated on the sides of the triangle of concentration in three-component diagrams of the state?

2. Are there any triple points inside the triangle of concentration in three-component diagrams of the state?

3. What can you say about triple points?

Assignments for SSDS 8

1. Three-component system MgO- Al₂O₃ –SiO₂.

2. Define the way of crystallization on the lines of polymorphic transformations.

№ 9

1. Can you show the way of crystallization in the state diagram in three-component system?

2. What can be defined by three-component diagram of the state?

3. Show the way of melting of any substance in three-component diagram of the state?

Assignments for SSDS 9

1. Three-component system CaO-MgO–SiO₂.

2. Define the way of crystallization in the system with immiscible fluids.

Sample list of themes of practical classes

1. Solution of tasks in diagrams of one-component systems state. Definition of number of phases, freedom degrees

2. Solution of practical tasks in two-component diagrams of the state. Definition of phase composition and qualitative content of phases in systems of silicate and other refractory materials.

3. Definition of phase changes in two-component systems at changing of temperature with the help of the state diagrams.

4. Estimation of tendency of fusions of silicate and other refractory materials to liquation.

5. Solution of practical tasks in three-component diagrams of the state. Definition of phase composition and qualitative content of phases in systems of silicate and other refractory materials.

6. Definition of phase changes in three-component systems at changing of temperature with the help of the state diagrams.

7. Solution of tasks in diagrams of three-component systems state. Definition of number of phases, freedom degrees.

8. Definition of ways of crystallization in diagrams of three-component systems state.

9. Definition of temperatures of sintering and melting in three-component mixtures.

Chapter 1

THE RULE OF PHASES AND ITS EMPLOYMENT

MAIN NOTIONS AND DEFINITIONS

The system. Physico-chemical system is a part of substance, chosen and removed in such way, that one can observe changes and finite conditions depending on defining terms in it. A phase is a part of a system, possessing identical chemical thermodynamic, physical properties. Neigbouring phases form boundary surface with each other.

Components. The components are chemically individual components of the system of less amount, that are sufficient to form any phase of equilibrium system.

Freedom degrees. Freedom degrees are independent thermodynamic parameters of phases of the system, which is in stable equilibrium, able to take arbitrary values in that interval, at which the number of phases doesn’t change.

The number of freedom degrees. The number of freedom degrees is the least number of independent parameters, necessary to define the system condition. The number of phases, number of components and number of freedom degrees are connected between each other by Gibb’s equation.

F + p = k + 2

where, F – number of freedom degree, p – number of phases, k – number of components.

In many cases silicate systems are condensed, and pressure has little influence on properties of such systems. Paying no regard to pressure, one can write in such cases

F + p = k + 1

While research equilibrium systems Clausius-Klapeiron equation has great significance, which describes volume change at phase transformations with temperature and critical heat.

Mathematically this dependence is expressed by equation:

where Q – heat of phase transformation; V₁ – specific volume of low temperature phase; V₂ – specific volume of high temperature phase; T – absolute temperature of phases equilibrium.

The equation (I,3) shows that if difference of specific volumes V₂ – V₁ is positive, that is at heating the volume increases, at presence of equation of positive quantity in the right part: temperature and latent heat of phase transformation (heat is evolved), the left part of equation will be positive.

Using equation (I,3) one can define the direction of the change of equilibrium pressure P depending on the change of equilibrium temperature and change quantity P on 1° temperature. This method of definition is suitable for any phases transformation, if only difference of phases volumes V₂ – V₁ and heat of this transformation are measurable.

For two-component systems the rule of phases takes the form

F + p = k + 2 = 2 + 2 = 4

At excluding vapour phase, and therefore pressure as changeable one, we get

F+ p = 2 + 1 = 3

At nonvariant condition of equilibrium system, when F = 0, maximum number of phases will be

p_max = 3

when the number of phases is minimal p = 1, maximum possibly number of freedom degrees

F_max = k + 1 – 1 = 2

Temperature and concentration of one of the components are independent parameters in such a system. The concentration of another component is defined by difference from 100 and is a dependent parameter.

The dependence between chemical, phase composition, temperature and concentration (in some cases pressure as well) is expressed by graphic diagrams of condition. Using them, one can define kind and number of phases, their composition and number of each in equilibrium condition at the given parameters and mixture compositions, and also changes of these characteristics when heated and cooled. At this the given changes must be considered as continuous chain from separate equilibriums.

At constant pressure the rule of phases for two-component systems gives the following correlations of phases numbers and freedom degrees:

Number of phases	Number of freedom degrees	Condition of systems	Geometric element of the diagram
1	2	Divariant	Field of stability
2	1	Monovariant	Boundary curve
3	0	Nonvariant	Nonvariant point

Example. Densities of liquid and solid tin at melting temperature (231,9°C) under pressure 1_atm correspondingly equal to 6,988 and 7,184 g/cm³. Melting heat of tin – 1690 cal/mole.

To define melting temperature of tin under pressure 100_atm.

Solution. We define the change of the temperature at increasing of pressure for 1_atm that is the quantity of , which is calculated from Clausius-Klapeiron (I,3)

where T – absolute melting temperature under the pressure 1_atm; (V₂ – V₁) – difference of volumes (specific) of liquid and solid tin, cm³/g; Q – specific melting heat of tin, cal/mole,

where 41,3 – l-atm^*; 118,7 – molecular weight of tin.

After we get

* 1 cal = 4,18·10³J = 41,3 l·atm

Melting temperature under the pressure – 100_atm

2. TWO-COMPONENT SYSTEMS

Two-component systems are divided into the following types: systems with eutectic melting, with chemical compounds, melted without decomposition; with chemical compounds, melted with decomposition; with chemical compounds, decomposed in solid form; polymorphous transformations of one of more crystalline phases, with liquation, systems with solid solutions of unlimited and limited miscibility – with eutectic or peritectic points.

Pic.1. The diagram of the state of systems MgO – SiO₂

Example 1. To define number, kind, phases and number of freedom degrees in the point a. In the diagram of condition of systems MgO – SiO₂ (pic. 1) representative point a of some mixture is given.

Solution. The point a is responsible for the composition of mixture 55% SiO₂ and 45% MgO, heated to the temperature 1800º and is in the field of liquid (of fusion). Therefore, the system has one liquid phase. The number of freedom degrees at the given conditions will be

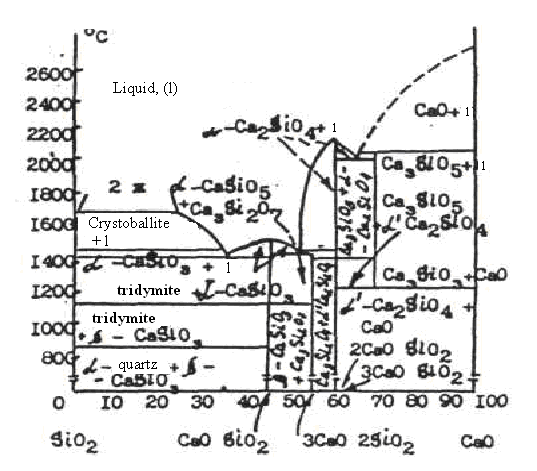
Pic.2. The diagram of the state of systems CaO – SiO₂

Example 2. The diagram of systems MgO – SiO₂ (see pic.1) for the composition 50% MgO and 50% SiO₂ the point b is given; to define number, kind of phases and number of freedom degree in it.

Solution. As the point is located on the liquidus line, liquid b is in equilibrium with solid phase 2MgOxSiO_2. therefore, there are two equilibrium phases.

The number of freedom degree F equals to

Example 3. To define the number, kind of phases and number of freedom degrees for eutectic point E in the diagram MgO – SiO₂ (see pic.1).

Solution. In eutectic point E solid phases MgO·SiO₂ , SiO₂ (cristobalite) and fusion of composition E – totally three phases are in equilibrium condition. The number of freedom degree F equals to

Example 4. To define number, kind of phases and number of freedom degree in representative point f in the CaO – SiO₂ diagram (pic.2).

Solution. The point f has composition 80% SiO₂ and 20% CaO. The mixture is heated to 1800º. The given mixture is fully in liquid (fused) condition. As the composition of initial mixture is in the field of liquation, fusion breaks down into liquids of two compositions. Thus, in equilibrium there are two liquid phases. The number of freedom degrees at this will be:

F=2+1-2=1