Зависимость мгновенного и истинного удлинений от относительного удлинения при деформации растяжения:

Относит. удлинение ε=Δl/lо	Мгновенное удлинение Δl/l	Истинное удлинение ε`=lnl/lo
0,01 (1%)	0,01 (1%)	0,01 (1%)
0,2 (20%)	0,167 (16,7%)	0,182 (18,2%)
1,0 (100%)	0,5 (50%)	0,693 (69,3%)

При разных видах деформации выполняются следующие соотношения: растяжение σ=Еε (закон Гука), где Е - коэффициент пропорциональности между σ и ε, называемый модулем Юнга; сдвиг τ=Gγ, где G – модуль сдвига; объемное сжатие р=В^.ΔV/V_o, где В – модуль объемной упругости. Упругие коэффициенты связаны между собой соотношениями: G=Е/2(1+μ); В=Е/3(1-2μ), где μ – коэффициент Пуассона. При μ=0,5 модуль Е=3G. Ниже приведены значения модуля Юнга для некоторых материалов в Па (ГПа): медь – 1,2^.10¹¹ (120); полистирол – 3^.10⁹ (3); мягкая резина – 2^.10⁶ (0,002).

При линейной упругости модуль Юнга (Е) определяют как тангенс угла наклона зависимости σ-ε (tgα). При нелинейной упругости он в процессе растяжения чаще уменьшается, и в этом случае пользуются величиной мгновенного (начального) модуля, который определяют как tg угла наклона касательной к этой кривой в начале координат. Иногда его определяют как тангенс угла наклона касательной к этой кривой в точке, соответствующей данному удлинению. Модуль Юнга является мерой жесткости материала. Величина, обратная ему (J=1/E), является мерой деформируемости материала и называется податливостью. Коэффициент Пуассона при растяжении является отношением уменьшения поперечных размеров образца к увеличению его продольных размеров. Если цилиндр длиной l_o и радиусом r уменьшается на Δr, тогда относительное удлинение равно Δl/l_о, а относительное уменьшение радиуса – Δr/r_о. Если объем образца не меняется, то Δl/l_о=2(Δr/r_о), т.е. относительный рост длины равен относительному сокращению поперечных размеров. Тогда коэффициент Пуассона μ=(Δr/r_о)/(Δl/l_о)=0,5. В случае идеальной упругости (ненаполненная резина) μ=0,5; для слабонаполненной резины μ=0,49. В пластмассах растяжение ведет к изменению структуры материала, включая расстояния между макромолекулами, и μ=0,2-0,4. В низкомолекулярных жидкостях упругость отсутствует, и μ=0.

2.2. Термодинамика высокоэластической деформации.

Способность обратимо деформироваться на десятки и сотни процентов является уникальным свойством эластомеров и верным признаком высокомолекулярной природы исследуемого образца. Механизм проявления эластичности можно понять, исследуя его термодинамическим методом.

Пусть образец эластомера длиной l₀ под действием напряжения f удлинился на величину dl. Для упрощения исключим явления вязкоупругости, обеспечивая действующему напряжению достаточное время для достижения равновесной деформации. Чтобы предотвратить необратимое перемещение макромолекул, возьмем слабо сшитый эластомер с редкой сеткой химических связей. Тогда деформация окажется полностью обратимой и равновесной, не зависящей от времени действия напряжения. Поскольку эластомеры при деформации практически не меняют объема, работа деформации обусловлена только действием приложенной силы: dA=fdl, а для равновесного процесса подведенная к системе теплота dQ=TdS. Согласно первому закону термодинамики, внутренняя энергия складывается из работы, совершенной над системой, и теплоты, подведенной к ней: dU=dA+dQ=fdl+TdS (2.1). Согласно второму закону термодинамики, внутренняя энергия системы складывается из свободной dF и связанной TdS: dU=dF+TdS (2.2). Подставляя (2.1) в (2.2), получим dF=fdl. При постоянных значениях температуры и объема выражение f=dF/dl раскрывает физический смысл деформирующей силы: она равна изменению свободной энергии системы в расчете на единицу удлинения. Определив значение dF из (2.2) и подставив его в последнее выражение, получим общее выражение для изменения термодинамических параметров эластомера в процессе деформации:

f=(dU/dl)-T(dS/dl), или f=f_U+f_S. (2.3).

Пространственно-сшитые эластомеры с малой частотой сетки при температуре существенно выше температуры стеклования Т_с ведут себя как идеальные эластомеры, в которых f_U=0. В идеальном эластомере возникающее при деформации напряжение обусловлено только изменением энтропии, происходящим за счет развертывания молекулярных клубков, что повышает ориентированность его структуры. Возникновение ориентации означает уменьшение беспорядка в системе, т.е. уменьшение энтропии: f=-T(dS/dl). При изотермическом сжатии газа, свойства которого близки к свойствам идеального газа, давление также меняется только за счет изменения энтропии: p=T(dS/dV). Поэтому и говорят, что упругость эластомера имеет газовую природу, так как напряжение при деформации обусловлено только изменением порядка в расположении элементов структуры: в идеальном эластомере - сегментов (частей) макромолекул, а в идеальном газе – молекул. Очевидно, что при малой деформации идеального кристалла, структура которого не нарушается, напряжение возникает только за счет изменения межатомных расстояний кристаллической решетки. Тогда для идеального кристалла f=(dU/dl).

По экспериментальной зависимости напряжения от температуры при разных удлинениях, полученной в равновесных условиях деформации, из уравнения (2.3) рассчитан вклад изменения свободной энергии и энтропии в величину напряжения реального эластомера. Оказалось, что в ненаполненных сетчатых эластомерах при комнатной температуре в широком диапазоне удлинений величина напряжения обусловлена главным образом изменением энтропии и лишь на 5-15% - изменением внутренней энергии (рис.2.3а). Только при малых удлинениях, когда энтропия меняется еще незначительно, вклад внутренней энергии в увеличение показателя напряжения достаточно велик. Чем ближе температура к температуре стеклования Т_с, т.е. чем больше эластомер по свойствам напоминает пластмассу, тем больше роль энергетической составляющей f_U и ее доля в общей величине силы (f_U/f). Это видно на примере пространственно сшитого полигексилметакрилата (Т_с=-3^оС), который при 100^ОС ведет себя как эластомер (f_U/f=0,26), а при 30^ОС приближается по свойствам к пластмассе, и f_U/f увеличивается до 0,97.

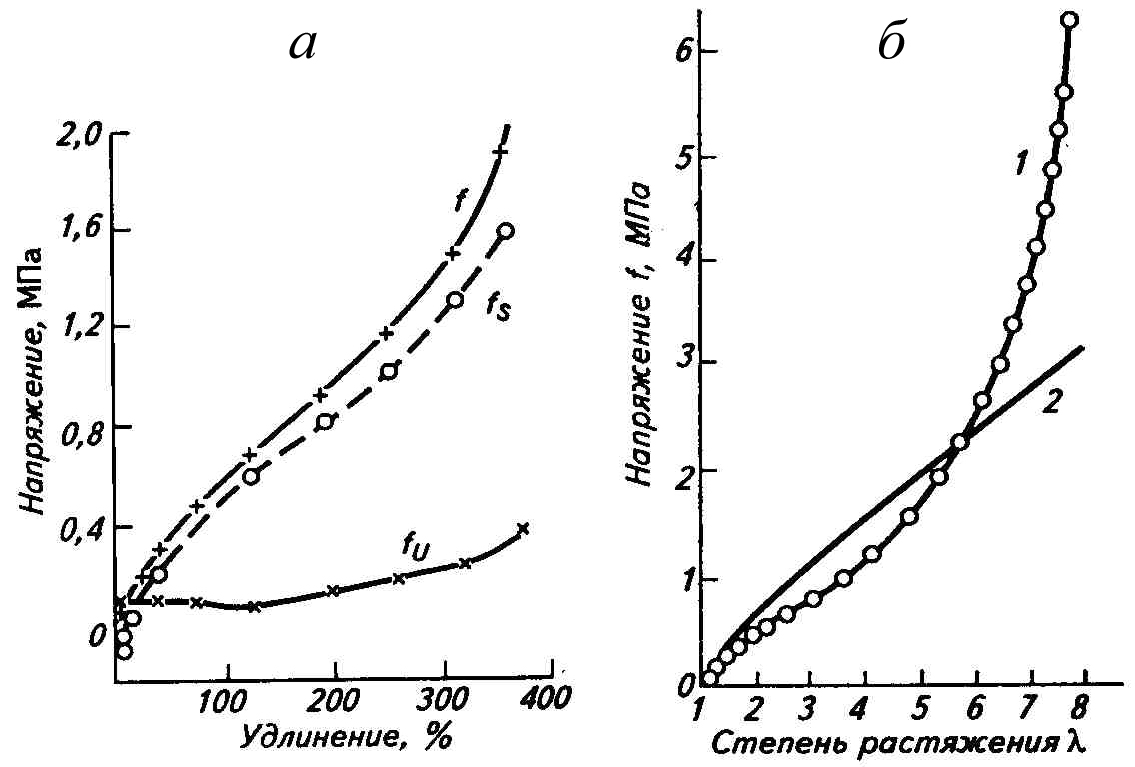
Рис.2.3. Экспериментальная кривая (а) напряжение-удлинение вулканизата НК

для равновесных условий (f) с изменением энтропийной (f_S) и энергетической (f_U) составляющих напряжения и сравнение (б) этой кривой (1) с теоретической кривой (2), построенной по уравнению f=G(λ-1/λ²).

Представления о существовании длинных гибких цепных макромолекул позволили применить к анализу деформационных свойств эластомеров законы статистической термодинамики и установить количественную связь между структурой макромолекулярного клубка и механическими свойствами. Для расчетов приняли наиболее простую модель свободносочлененной цепи. Чтобы учесть заторможенность вращения, ввели понятие сегмента как жесткого элемента структуры, а соединения между сегментами приняли свободно сочлененными. Тогда можно подобрать такую длину сегмента l или такое их число n, чтобы при общей длине эквивалентной цепи расстояние между ее концами r было бы таким же, как для реальной макромолекулы. Для идеального эластомера с учетом зависимости напряжения от изменения энтропии (f=dF/dl) получили уравнение зависимости напряжения от относительной деформации r/r_o для отдельной макромолекулы: f=-T(dS/dr)_T=(2kT/r_o)r/r_o, по которму легко определяется коэффициент пропорциональности между ними G, называемый модулем эластичности макромолекулы: G=2kT/r_o=3kT/nl². Из этой формулы следует, что модуль эластичности макромолекулярного клубка растет с повышением температуры (G-T). Объясняют это тем, что растянутый клубок стремится вернуться в прежнее (до деформации) наиболее вероятное состояние, и возвращающая сила тем больше, чем выше температура и больше интенсивность теплового движения сегментов. Здесь видна полная аналогия с газом: повышение температуры увеличивает его давление на поршень благодаря интенсификации теплового движения и росту частоты ударов молекул по поршню. Поэтому равновесную упругость макромолекул называют «газовой упругостью». Различие лишь в том, что тепловое движение сегментов направлено на сокращение клубка, а газа - на расширение.

Статистическая теория высокоэластической деформации математически описывает экспериментальную кривую только до деформации 50% (рис.2.3б). Несовпадение с экспериментальной кривой при более высоких деформациях объясняется несовершенством как пространственной сетки (дефектами структуры), так и самой теории, не позволяющей количественно описать зависимость свободной энергии dF от деформации. Поэтому эта теория не может быть использована для прогнозирования качества изделий. Принципиальное значение статистической теории состоит в том, что она дает понимание молекулярного механизма проявления высокоэластичности, объясняет основную причину упругости и появления напряжения стремлением макромолекул перейти в наиболее вероятное состояние статистического клубка, когда достигается максимум энтропии и минимум свободной энергии.

В последние годы активизировались работы по математическому и компъютерному моделированию поведения изделий из эластомеров для решения прикладных задач повышения ресурса работы по отдельным показателям их качества. Разрабатываются молекулярные механизмы и микромеханические модели уменьшения сопротивления качению, повышения сопротивления образованию и разрастанию трещин и улучшения других показателей качества автомобильных шин, которые дают возможность прогнозирования срока их службы методом конечных элементов.