Модуль 2. Физические свойства полимеров.

2.1. Физические и фазовые состояния и переходы.

Наличие барьера вращения вокруг простой С-С-связи в главной цепи макромолекулы и существование узлов флуктуационной сетки в массе полимера обуславливают ряд особенностей в изменении его механических свойств от температуры. Соотношение между величиной барьера вращения и величиной флуктуаций тепловой энергии зависит от температуры. При низкой температуре величина флуктуаций тепловой энергии становится настолько малой, что не преодолевает барьер вращения, и макромолекула теряет способность к деформации. Чем более гибкие макромолекулы, тем до более низкой температуры полимер остается эластичным.

Термомеханическая кривая имеет форму зависимости деформируемости полимера от температуры (рис.2.1) и информирует не столько о свойствах полимера при данной температуре, сколько о его структуре. При низкой температуре (область Iа) деформация мала и слабо увеличивается, так как аморфный полимер, подобно стеклу, находится в стеклообразном состоянии. Начиная с температуры стеклования Т_с, деформация растет (переходная область IIа) и достигает нескольких десятков, а при снятии кривой в режиме растяжения – и сотен процентов. При дальнейшем нагревании деформация снова мало зависит от температуры, так как полимер перестает быть стеклообразным, но и не стал еще эластичным. Поэтому он деформируется вяло, как натуральная кожа или линолеум. При температуре выхода на плато (область IIIа) полимер переходит в развитое высокоэластическое состояние, в котором он легко деформируется при действии силы и быстро возвращается в исходное положение после снятия нагрузки. Температура начала деформации вязкого течения (изгиб на кривой), называется температурой текучести Т_т, выше которой полимер находится в вязкотекучем состоянии (область IVа). Если полимер состоит из макромолекул с регулярной структурой, то ближний порядок в расположении сегментов может перейти в дальний порядок, и возникнет кристаллическая структура, которая оказывается жесткой и малодеформируемой даже при степени кристалличности 30-35%. Полимер кристаллической структуры, например полиэтилен, обнаруживает свойства пластмассы, даже если его температура стеклования ниже комнатной (-70^оС), а при температуре плавления кристаллитов 110-135^ОС (Т_пл>Т_т) сразу переходит в вязкотекучее состояние (кривая 1б). Полимеры с Т_т>Т_пл>Т_с сначала переходят в высокоэластическое, а затем – в вязкотекучее состояние (кривая 2б).

а б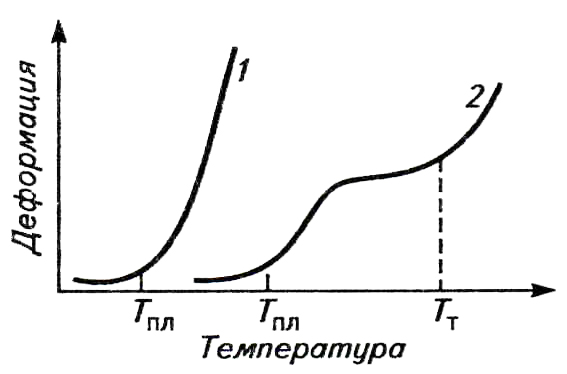

Рис.2.1. Термомеханические кривые аморфных (а) и кристаллических (б) полимеров:

I - стеклообразное состояние; II - переходная область; III - высокоэластическое состояние;

IV - вязкотекучее состояние (звездочкой отмечена точка начала термодеструкции).

Назначение термомеханической кривой полимера состоит в определении температурных пределов существования его физических (релаксационных) состояний - стеклообразного, высокоэластического и вязкотекучего, каждое из которых имеет определенное значение при его переработке или применении. Высокоэластическая деформация мало зависит от температуры и связана с изменением формы макромолекулярных клубков. Деформация вязкого течения связана со значительными смещениями сегментов относительно положения равновесия, приводящими к перемещению клубков друг относительно друга. Очень важно, что при температуре ниже Т_с полимер сохраняет некоторый комплекс свойств и не становится хрупким, но может быть охлажден до температуры хрупкости Т_хр, когда легко разбивается при ударе. На термо-механической кривой Т_хр не проявляется в виде характерной точки, а методы ее определения всегда связаны с разрушением образца. Если область Т_с-Т_хр протяженна и включает комнатную температуру, то полимер будет применяться как пластмасса (термопласт), а при совпадении комнатной температуры с областью Т_т-Т_с полимер найтет применение в качестве эластомера (каучука).

В стеклообразном или высокоэластическом состояниях полимер под действием силы тяжести сохраняет свою форму, что характерно для твердого агрегатного состояния. В вязкотекучем состоянии то под действием силы тяжести он медленно растекается, что соответствует жидкому агрегатному состоянию. Газообразного состояния полимеры не могут иметь из-за большой длины макромолекул. Энергия межмолекулярного взаимодействия в расчете на одну макромолекулу настолько велика, что превышает энергию разрыва химических связей в основной цепи. Поэтому термодеструкция полимера идет легче, чем превращение его в газообразное состояние. Поскольку полимеры не испаряются, то межмолекулярное взаимодействие оценивают не теплотой испарения, а плотностью энергии когезии или параметром растворимости. Таким образом, особенности молекулярной и надмолекулярной структуры полимеров проявляются в характерной только для них зависимости свойств от температуры и обуславливают возможность существования их в трех физических и только двух агрегатных состояниях.

При эксплуатации изделия из полимеров подвергаются воздействию растяжения, сдвига и объемного сжатия (рис.2.2). В первом случае деформацию оценивают степенью растяжения λ=l/l_о и относительным удлинением при растяжении ε=(l-1)/l_о=Δl/l_о. При сдвиге деформация γ=Δl/l_о и расстояние l_о не изменяется, а при объемном сжатии (например, гидравлическое сжатие) деформация оценивается по коэффициенту сжимаемости β=ΔV/V_o.

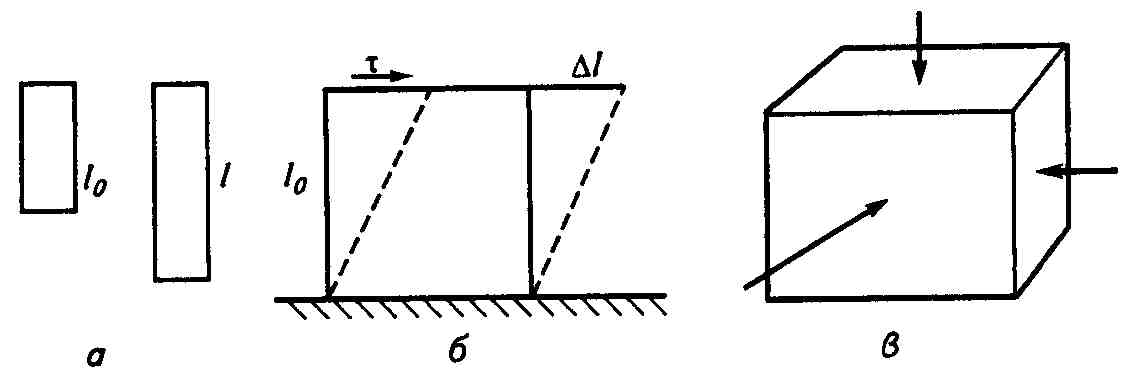
Рис.2.2. Виды деформаций полимеров:

а - растяжение; б - сдвиг; в - объемное сжатие.

При растяжении образца полимера мгновенное удлинение dε`=dl/l; ε`=lnl/l_o. Если образец длиной 1 см удлинился на 1 см, то ε=Δl/l_о=1/1=1 (т.е. 100%). Теперь образец стал длиной 2 см; снова удлиняем его на Δl/l=1 см. Общее удлинение образца стало 2 см. Теперь ε=Δl/l_о=2/1=2 (т.е. 200%), а мгновенное удлинение ε`=Δl/l=1/2=0,5 (т.е. 50%). Различия между удлинениями ε` и ε показывают, что при постоянной скорости движения зажима динамометра скорость фактической деформации уменьшается со временем, что можно заметить только при больших деформациях (табл. 2.1). Если радиус цилиндрического образца в исходном состоянии равен r_o, а внешняя деформирующая сила - Р, то в расчете на исходное сечение (πr_o²) напряжение f=Р/πr_o². При удлинении в два раза сила Р действует на вдвое меньшее сечение, вызывая вдвое большее напряжение. В расчете на истинное сечение напряжение σ=Р/(πr²) при σ=λf.

Таблица 2.1.