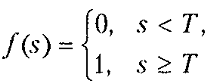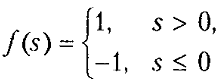Лабораторная работа 1 Искусственные нейроны и нейронные сети
Цель: Изучить модель искусственного нейрона и модели нейронных сетей, алгоритмы их обучения
1. Теоретические сведения
1.1. Искусственные нейроны
Под нейронными сетями подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Адаптируемые и обучаемые, они представляют собой распараллеленные системы, способные к обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон (рисунок 1), или просто нейрон, называемый так по аналогии с биологическим прототипом.
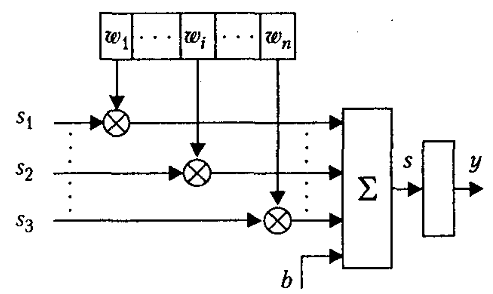
Рисунок 1. Структура искусственного нейрона
В состав нейрона входят умножители (синапсы), сумматор и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи, - вес синапса. Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента – выхода сумматора. Эта функция называется функцией активации или передаточной функцией нейрона.
Математическая модель нейрона описывается соотношениями:

![]()
где
 – вес синапса (i=1..n);
b – значение смещения; s
– результат суммирования;
– вес синапса (i=1..n);
b – значение смещения; s
– результат суммирования;
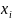 - компонент входного вектора (входной
сигнал) (i=1..n);
y – выходной сигнал
нейрона; n – число входов
нейрона; f – нелинейное
преобразование (функция активации или
передаточная функция).
- компонент входного вектора (входной
сигнал) (i=1..n);
y – выходной сигнал
нейрона; n – число входов
нейрона; f – нелинейное
преобразование (функция активации или
передаточная функция).
Таблица 1
Перечень функций активации нейрона
Название |
Формула |
Область значений |
Пороговая |
|
[0;1] |
Знаковая |
|
[-1;1] |
Сигмоидальная |
|
[0;1] |
Линейная |
|
|
Гаусова (радиальная базисная функция) |
|
(0;1) |
1.2. Искусственные нейронные сети
Персептрон
Персептроном называется простейшая нейронная сеть. Персептрон состоит из единственного слоя, включающего S нейронов (рисунок 2).
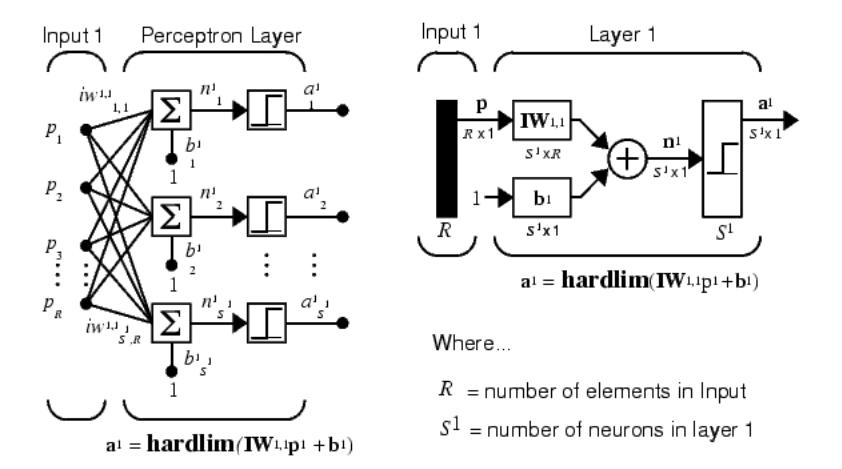
Рисунок 2. Архитектура персептрона
Нейрон, используемый в модели персептрона, имеет ступенчатую функцию активации hardlim с жесткими ограничениями. Каждое значение элемента вектора входа персептрона умножено на соответствующий вес w1j, и сумма полученных взвешенных элементов является входом функции активации. Если вход функции активации n ≥ 0, то нейрон персептрона возвращает 1, если n < 0, то 0. Функция активации с жесткими ограничениями придает персептрону способность классифицировать векторы входа, разделяя пространство входов на две области (рисунок 3), для персептрона с двумя входами и смещением.
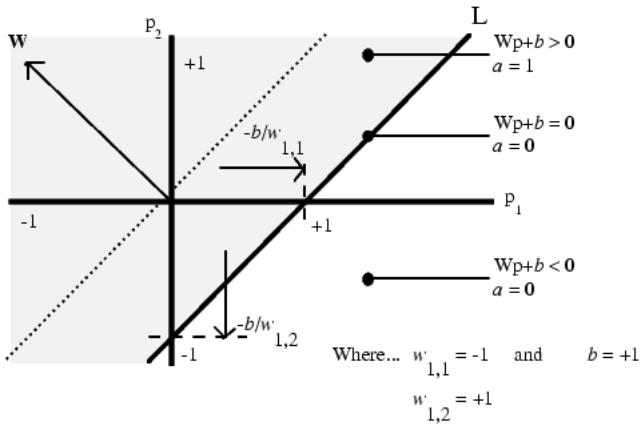
Рисунок 3. Деление области значений
Пространство входов делится на две области разделяющей линией L, которая для двумерного случая задается уравнением
WT p + b = 0
Эта линия перпендикулярна к вектору весов w и смещена на величину b. Векторы входа выше линии L соответствуют положительному потенциалу нейрона, и, следовательно, выход персептрона для этих векторов будет равен 1; векторы входа ниже линии L соответствуют выходу персептрона, равному 0. При изменении значений смещения и весов граница линии L изменяет свое положение.
Персептрон без смещения всегда формирует разделяющую линию, проходящую через начало координат; добавление смещения формирует линию, которая не проходит через начало координат. В случае, когда размерность вектора входа превышает 2, т. е. входной вектор Р имеет более 2 элементов, разделяющей границей будет служить гиперплоскость.
Уравнение однослойного персептрона имеет вид
a = f (Wp + b).
Сеть Кохонена
Сеть Кохонена представляет собой слой Кохонена, который функционирует по правилу «победитель получает все». Для заданного входного вектора только один нейрон Кохонена выдает логическую единицу, все остальные выдают нули.
Выход каждого нейрона Кохонена является просто суммой взвешенных элементов входных сигналов:
![]()
где
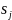 - выход j-го нейрона
Кохонена;
- выход j-го нейрона
Кохонена;
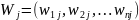 - вектор весов j-го нейрона
Кохонена;
- вектор весов j-го нейрона
Кохонена;
 - вектор входного сигнала.
- вектор входного сигнала.
Нейрон Кохонена с максимальным значением является «победителем». Его выход равен единице, у остальных он равен нулю.