1.3 Статистичне дослідження результатів спостережень

Статистичне дослідження результатів спостережень (встановлення характеру розподілу) заключається у визначенні чисельних характеристик статистичного розподілу, висуненні гіпотези про відповідність даного статистичного розподілу до одного з теоретичних законів та перевірці згоди кривих статистичного та теоретичного розподілів за відповідними критеріями.

У даній роботі необхідно встановити основні чисельні характеристики статистичного розподілу:

а) статистичне середнє (оцінка математичного сподівання) випадкової величини, розраховане за даними таблиці 1.6,

. (1.5)

Статистичне середнє ще називають центром розподілу. На відміну від середнього арифметичного значення, що було підраховано за формулою (1.1), статистичне середнє є числом, яке пов’язане із законом розподілу випадкової величини, а тому є більш обґрунтованим;

б)статистична дисперсія випадкової величини, яка розраховується за допомогою таблиці 1.6,

; (1.6)

Дисперсія є середнім квадратом відхилення випадкової величини від її центру розподілу;

в)середнє квадратичне відхилення, яке ще називають стандартним відхиленням,

. (1.7)

Для кривої нормального розподілу стандартне відхилення σ_(X) з точки зору графічної інтерпретації відповідає точці перегину від опуклості до увігнутості;

г)коефіцієнт варіації випадкової величини

, (1.8)

який характеризує відносну величину середнього квадратичного відхилення, тобто ступінь розсіювання масиву спостережень відносно центру розподілу;

д)коефіцієнт нерівномірності випадкової величини

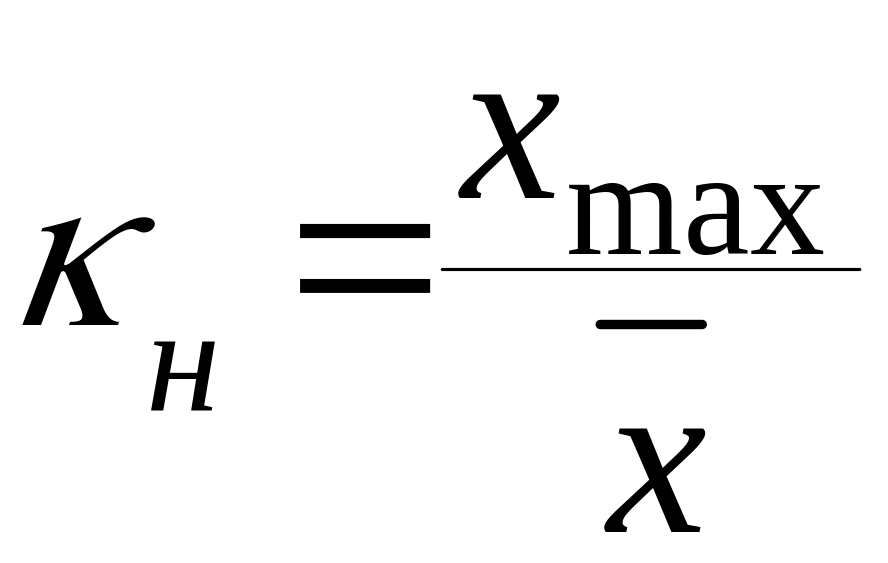. (1.9)

При висуненні гіпотези про відповідність даної випадкової величини до теоретичного закону, який би із достатньою точністю описував статистичний розподіл випадкової величини, виходять із: а) фізичної суті процесу, явища або об’єкту, що досліджується, б) результатів попередніх досліджень даної величини, які опубліковані в науково-технічній літературі, в) з вигляду графічної залежності у формі гістограми [1, 2, 3].

При цьому враховують також додаткові ознаки, які є характерними для деяких чисельних характеристик статистичного розподілу, наприклад:

а) для нормального розподілу розсіювання значень даної виборки укладається у межах інтервалу

(1.10)

б) для розподілу Пуасона характерним є співвідношення

; (1.11)

в) для експоненційного розподілу

. (1.12)

Для перевірки гіпотези про теоретичний закон розподіл випадкової величини використовуються критерії узгодженості, наприклад, χ² (критерій Пірсона)

. (1.13)

Найбільш поширеними функціями розподілу випадкових величин основних показників експлуатаційної роботи залізниць вважаються:

а) для неперервних випадкових величин:

1) нормальний закон розподілу зі щільністю

; (1.14)

2) експоненційний закон розподілу із щільністю

; (1.15)

3) закон розподілу Ерланга k-го порядку (k=1, 2, 3, 4…)

; (1.16)

б) для дискретних випадкових величин:

1) закон розподілу Пуасона

; (1.17)

2) гіпергеометричний розподіл

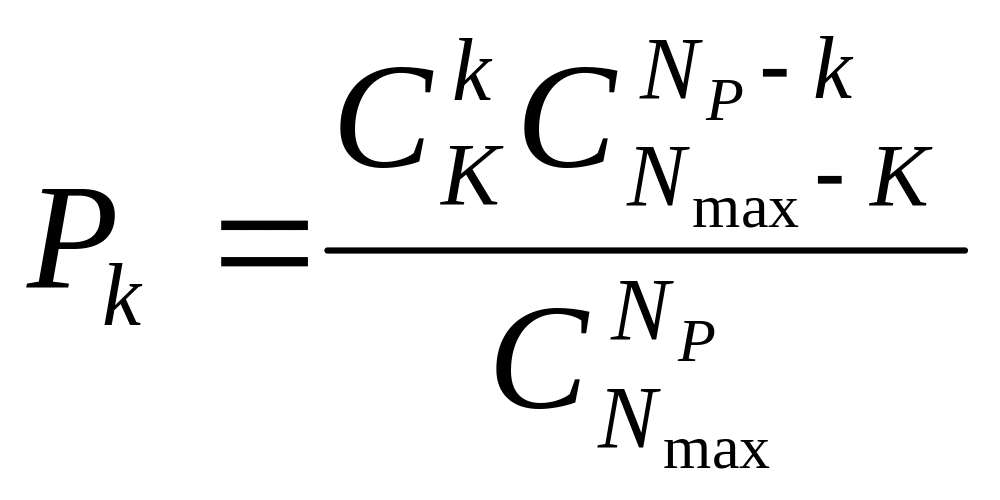, (1.18)

де -відповідно сполучення з

елементів по

елементів,

. (1.19)

Аналогічно визначаються і інші сполучення цієї групи