Правила вычисления производных.
Задание |
Ответы |
|||
Вариант I |
1 |
2 |
3 |
4 |
f(х)=(3+4x) (4x-3). Найдите f(-1) |
-32 |
32 |
50 |
-50 |
g(x)=2x Найдите g |
1,75 |
3,5 |
1,4 |
7 |
Найдите
|
-2 |
4 |
-4 |
2 |
.
.
Правила вычисления производных.
Задание |
Ответы |
|||
Вариант II |
1 |
2 |
3 |
4 |
f(х)=(2-5x)(5x+2). Найдите f(-1) |
-32 |
32 |
50 |
-50 |
g(x)=5x Найдите g |
1,75 |
3,5 |
1,4 |
7 |
Найдите |
-2 |
4 |
-4 |
2 |
.
.
Правила вычисления производных. Верный ответ: вариант 1 – 1, 2, 3; вариант 2 – 3, 4, 1.
|
Метод интервалов.
Задание |
Ответы |
|||
Вариант I. |
1 |
2 |
3 |
4 |
Решите неравенство:
|
(-1;1) |
(-1;0)U(0;1) |
(-2;2) |
(-∞;2)U(2;∞) |
|
(-3;-2)U(2;∞) |
(-∞;-2)U(2;∞) |
(-1;1) |
(-3;1) |
<
0
>
0
Метод интервалов.
Задание |
Ответы |
|||
Вариант I. |
1 |
2 |
3 |
4 |
Решите неравенство:
|
(-1;1) |
(-1;0)U(0;1) |
(-2;2) |
(-∞;2)U(2;∞) |
|
(-3;-2)U(2;∞) |
(-∞;-2)U(2;∞) |
(-1;1) |
(-3;1) |
>
0
<
0
Метод интервалов. Верные ответы: вариант 1 – 2, 1; вариант 2 – 4, 3.
|
Касательная к графику функции.
Задание |
Ответы |
|||
Вариант I. |
1 |
2 |
|
|
Найдите угол наклона касательной к
графику функции f(x) в точке его с
абсциссой
f(x)=2 |
30° |
135° |
60° |
45° |
Напишите уравнение касательной к графику функции f(x) в точке его с абсциссой =0: f(x)=2 +1. |
y= - 1 |
y=2 |
y=1 |
y= - 2. |
:
,
=-0.25Касательная к графику функции.
Задание |
Ответы |
|||
Вариант II. |
1 |
2 |
|
|
Найдите угол наклона касательной к графику функции f(x) в точке его с абсциссой : f(x)= - 2 , =-0.25 |
30° |
135° |
60° |
45° |
Напишите уравнение касательной к графику функции f(x) в точке его с абсциссой =0: f(x)=2 - 1. |
y= - 1 |
y=2 |
y=1 |
y= - 2. |
Касательная к графику функции. Верные ответы: вариант 1 – 2, 3; Вариант 2 – 4, 1.
|
Касательная к графику функции.
Задание |
Ответы |
|||
Вариант I. |
1 |
2 |
|
|
Найдите угол наклона касательной к графику функции f(x) в точке его с абсциссой : f(x)=2 , =-0.25 |
30° |
135° |
60° |
45° |
Напишите уравнение касательной к графику функции f(x) в точке его с абсциссой =0: f(x)=2 +1. |
y= - 1 |
y=2 |
y=1 |
y= - 2. |
Касательная к графику функции.
Задание |
Ответы |
|||
Вариант II. |
1 |
2 |
|
|
Найдите угол наклона касательной к графику функции f(x) в точке его с абсциссой : f(x)= - 2 , =-0.25 |
30° |
135° |
60° |
45° |
Напишите уравнение касательной к графику функции f(x) в точке его с абсциссой =0: f(x)=2 - 1. |
y= - 1 |
y=2 |
y=1 |
y= - 2. |
Касательная к графику функции. Верные ответы: вариант 1 – 2, 3; Вариант 2 – 4, 1.
|
Производная сложной функции.
Задания |
Варианты ответов |
|||
Вариант I. |
1 |
2 |
3 |
4 |
f Найти f(-2). |
-52 |
-60 |
30 |
-24 |
f Найти D(f). |
(-∞;-7)U(-7;-5)U (5;∞) |
(-5;5) |
(-∞;3)U(3;+∞) |
(-5;5) x≠7 |
f
g Составьте:
|
a)
b) |
a)
b) |
a)
b) |
a)
b) |
;
.
Производная сложной функции.
Задания |
Варианты ответов |
|||
Вариант II. |
1 |
2 |
3 |
4 |
f Найти f(-1). |
-52 |
-60 |
30 |
-24 |
f Найти D(f). |
(-∞;-7)U(-7;-5)U (5;∞) |
(-5;5) |
(-∞;3)U(3;+∞) |
(-5;5) x≠7 |
f g . Составьте:
|
a)
b) |
a)
b) |
a)
b) |
a)
b) |
;
Производная сложной функции Верные ответы: вариант I – 4,1,2,3; вариант II – 2,3,4,2.
|
Производная тригонометрических функций.
Найдите производную |
||||
Задания |
Варианты ответов |
|||
Вариант I. |
1 |
2 |
3 |
4 |
f(x)= sin2x--cos3x |
cos2x-sin3x |
2sin3x-3cos3x |
-2sin2x-3cos3x |
2cos2x+3sin3x |
f(x)=tgx-ctg(x+ |
|
|
|
|
f(x)= |
2sinxcosx |
-2sin2x |
sin2x |
2cosx |
)
Производная тригонометрических функций Верные ответ: вариант I – 4,2,3; вариант II – 3,4,2.
|
Производная тригонометрических функций.
Найдите производную |
||||
Задания |
Варианты ответов |
|||
Вариант I. |
1 |
2 |
3 |
4 |
f(x)= cos2x -sin3x |
cos2x-sin3x |
2sin3x-3cos3x |
-2sin2x-3cos3x |
2cos2x+3sin3x |
f(x)=ctgx+ +tg(x- ) |
|
|
|
|
f(x)= |
2sinxcosx |
-2sin2x |
sin2x |
2cosx |
Вариант 1.
Решите уравнение:
Вычислите:
А) -30°.
В) 145°.
С) 30°.
D) 60°.
E) -45°.
3. Найдите значение производной функции:
у(х)=tg x при
х=
.
Найдите область определения функции:
у=
Какая из функций в области определения
является чётной?
f(x)=x7-4x5+2x-1. Найдите f '(x).
A) x7-20x3+2.
B) 7x6-20x4+2.
C) x7-20x4-1.
D) x7-20x+2.
E) 7x6-20x5+2x-1.
7. Вычислите:
,
если
.
A) ½.
B) 1½.
C) 2½.
D) ¾.
E) 4/9.
8. Упростите:
На отрезке прямой у=
,
отсекаемом осями координат, количество
точек с целыми координатами равно
А) 4.
В) 3.
С) 0.
D) 2.
E) 1.
10. Вычислите площадь параллелограмма,
построенного на векторах
Вариант 2.
Решите уравнение:
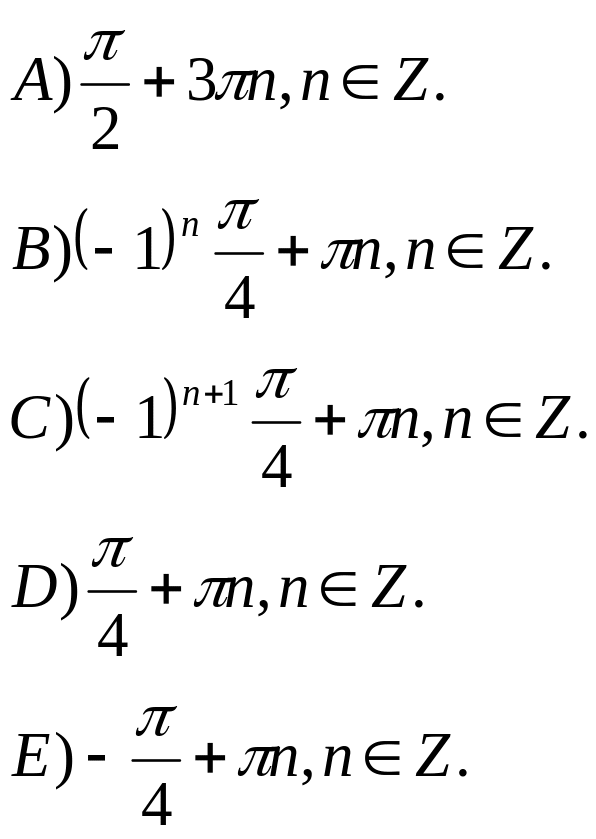
Найдите производную функции
А) х.
В) 3х4.
С) 11х4.
D) 7x4.
E) x4-7.
3. Исследуйте функцию f(x)=-x2 +7x на экстремум:
A) х=3,5, точка максимума.
B) х=1, точка минимума.
C) х=3,5, точка минимума.
D) х=7, точка максимума.
E) х=0, точка минимума.
4. Вычислите:
А) 1.
В) 0,97.
С) 0,99.
D) 0,96.
E) 0,98.
5. Вычислите f '(0)+f '(-1), если
f(x)=13x2-7x+5.
A) -40.
B) 12.
C) 30.
D) 25.
E) -10.
6. Решите уравнение:
А) Нет решений.
Упростите:
Составьте уравнение касательной к
графику функции у=cos2x
в точке
Найдите производную функции у=2,5х2-х5.
А) 12,5х-х4.
В) 2,5х2-5х4.
С) 5х-5х4.
D) 5x-x5.
E) -5x+5x4.
10. Найдите
А) 20.
В) 19.
С) 22.
D) 18.
E) 21.