
- •Числові ряди
- •Приклад . Ряд розбігається, тому що . Приклад . Ряд розбігається. Маємо
- •Приклад. Розглянемо ряд , де q – довільне число. Неважко бачити, що послідовність 1, q, q 2, … q n… є геометричною прогресією із знаменником q. Відомо, що , отже
- •Загальні властивості рядів
- •Необхідна умова збіжності ряду.
- •Приклад. Ряд розбігається, оскільки .
- •Ознаки збіжності рядів з додатними членами
- •Знакозмінні ряди.
- •Знакопереміжні ряди
- •Теорема Лейбніца: Знакопереміжний ряд збігається, якщо:
- •Приклад. Обчислити наближено суму ряду , взявши чотири його члени, та оцінити похибку. Виконуючи обчислення, отримаємо
- •Функціональні ряди
- •Степеневі ряди Степеневі ряди – це функціональні ряди, що мають вигляд
- •Диференціювання та інтегрування степеневих рядів
- •За допомогою цих властивостей можна одержати важливі результати, наприклад, знайти суми деяких рядів.
- •Ряди Тейлора
- •Ряди Фур’є
- •Варіанти завдань
- •Розв’язання завдань
- •Перевіримо необхідну умову збіжності ряду (2):
- •Список літератури
Варіанти завдань
Завдання 1.
Дослідити
на збіжність ряд
![]() ,
якщо загальний член ряду
,
якщо загальний член ряду
![]() має вигляд
має вигляд
1. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() г)
г)
![]()
2. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
3. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
4. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ; г)
; г)
![]()
5. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
6. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
7. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
8. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
9. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)![]()
10. а)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
11. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
12. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
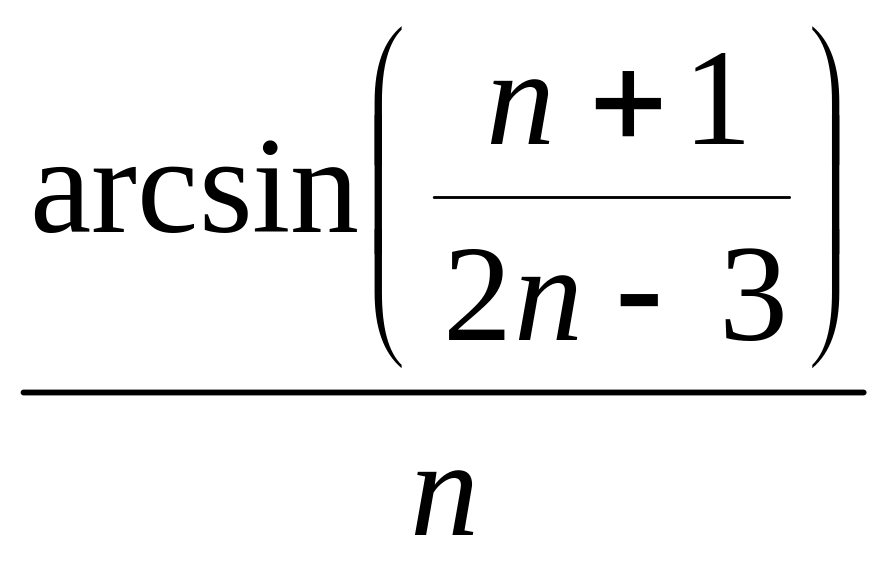
13. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
14. a)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;г)
;г)
![]()
15. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
 ;
г)
;
г)
![]()
16. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;г)
;г)
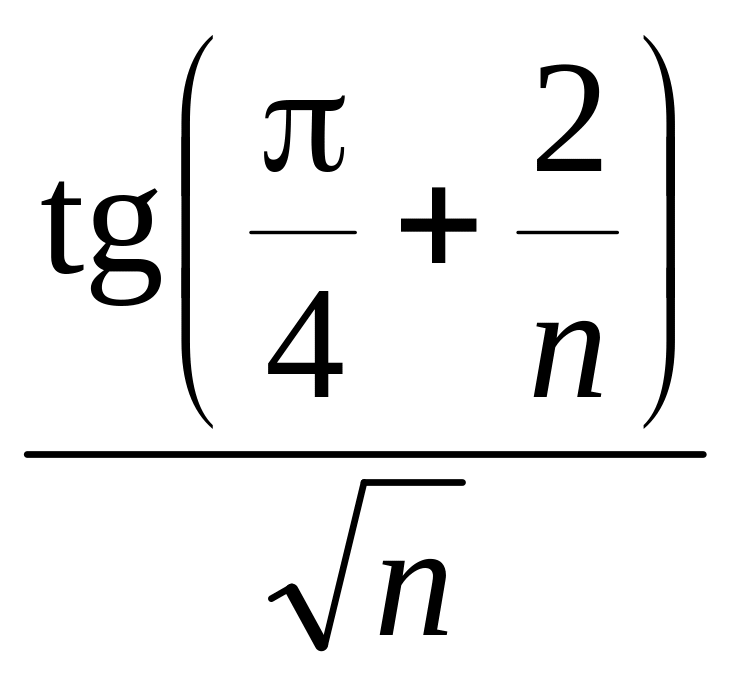
17. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
 ;
г)
;
г)
![]()
18. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
19. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
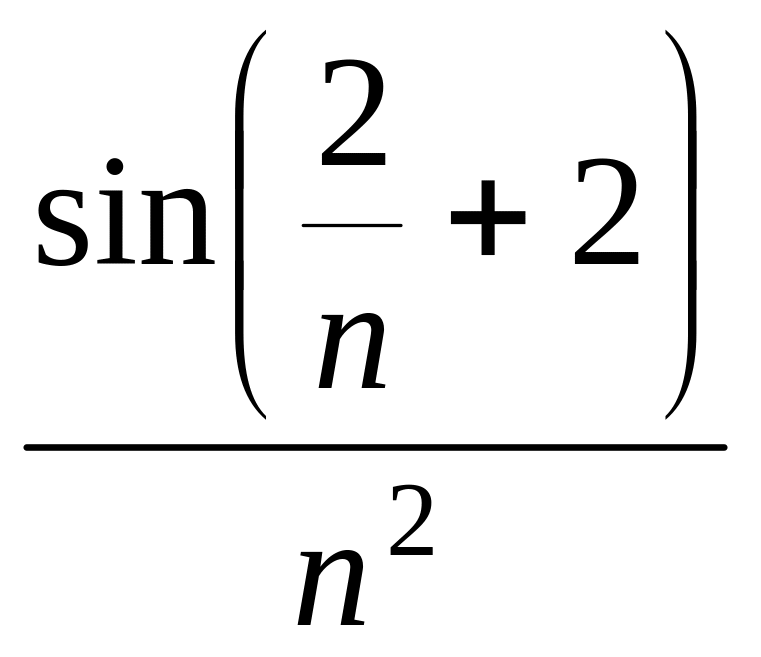
20. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
21. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
22. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
23. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
24. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
25. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
26. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;г)
;г)![]()
![]()
27. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
28. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
29. а)
![]() ;
б)
;
б)
![]() ; в)
; в)
![]() ;
г)
;
г)
![]()
30. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ; г)
; г)
![]()
Завдання 2.
Записати
три перші члени ряду
![]() й дослідити його на абсолютну та умовну
збіжність, якщо
має вигляд
й дослідити його на абсолютну та умовну
збіжність, якщо
має вигляд
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)
![]()
17)
![]()
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
![]()
30)
![]()
Завдання 3.
Задано
загальний член
![]() степеневого ряду
степеневого ряду
![]() .
Записати явно часткову суму
.
Записати явно часткову суму
![]() .
Знайти область збіжності ряду.
.
Знайти область збіжності ряду.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)
![]()
17)
![]()
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28) ![]()
29)
![]()
30)
![]()
Завдання 4.
Наближено
обчислити наступні значення, використовуючи
3 члени розкладу функцій у ряд Маклорена.
Оцінити похибку. Вважати, що
![]() .
.
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
10)
![]()
11)
![]()
12)
![]()
13)
![]()
14)
![]()
15)
![]()
16)
![]()
17)
![]()
18)
![]()
19)
![]()
20)
![]()
21)
![]()
22)
![]()
23)
![]()
24)
![]()
25)
![]()
26)
![]()
27)
![]()
28)
![]()
29)
![]()
30)
![]()
Завдання 5.
Наблизити
функцію квадратним тричленом у околі
точки
![]() за допомогою розкладу її у ряд Маклорена
за допомогою розкладу її у ряд Маклорена
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]() 15)
15)
![]()
16)
![]() 17)
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]() 21)
21)
![]()
22)
![]() 23)
23)
![]() 24)
24)
![]()
25)
![]() 26)
26)
![]() 27)
27)
![]()
28)
![]() 29)
29)
![]() 30)
30)
![]()
Завдання 6.
Обчислити
наближено інтеграл
![]() ,
взявши 4 члени розкладу у степеневий
ряд підінтегральної функції. Оцінити
похибку.
,
взявши 4 члени розкладу у степеневий
ряд підінтегральної функції. Оцінити
похибку.
№ |
|
а |
№ |
|
а |
№ |
|
а |
№ |
|
а |
1 |
|
0,7 |
2 |
|
0,3 |
3 |
|
0,2 |
4 |
|
0,1 |
5 |
|
0,8 |
6 |
|
0,4 |
7 |
|
0,5 |
8 |
|
2 |
9 |
|
0,6 |
10 |
|
0,9 |
11 |
|
0,2 |
12 |
|
0,3 |
13 |
|
0,6 |
14 |
|
0,5 |
15 |
|
0,5 |
16 |
|
0,7 |
17 |
|
0,5 |
18 |
|
0,3 |
19 |
|
0,6 |
20 |
|
0,3 |
21 |
|
0,8 |
22 |
|
0,9 |
23 |
|
0,5 |
24 |
|
0,8 |
25 |
|
0,5 |
26 |
|
0,8 |
27 |
|
1,0 |
28 |
|
0,2 |
29 |
|
0,3 |
30 |
|
0,1 |
|
|
|
|
|
|
Завдання 7.
Знайти
наближений розв’язок задачі Коші
![]() за допомогою розкладу невідомої функції
у ряд Тейлора обмежившись трьома членами
розкладу
за допомогою розкладу невідомої функції
у ряд Тейлора обмежившись трьома членами
розкладу
1)
![]() 16)
16)
![]()
2)
![]() 17)
17)
![]()
3)
![]() 18)
18)
![]()
4)
![]() 19)
19)
![]()
5)
![]() 20)
20)
![]()
6)
![]() 21)
21)
![]()
7)
![]() 22)
22)
![]()
8)
![]() 23)
23)
![]()
9)
![]() 24)
24)
![]()
10)
![]() 25)
25)
![]()
11)
![]() 26)
26)
![]()
12)
![]() 27)
27)
![]()
13)
![]() 28)
28)
![]()
14)
![]() 29)
29)
![]()
15)
![]() 30)
30)
![]()
Завдання 8.
Періодичний з періодом 2l прямокутний імпульс f(x) є заданим на півперіоді (0, l) формулою
![]() .
.
Побудувати графік f(x) на інтервалі (-2l, 2l), продовжуючи f0(x) як парну функцію для парних номерів завдання, і як непарну – для непарних номерів.
Розкласти f(x) у ряд Фур’є.
Записати
тригонометричні многочлени
![]() ,
що наближують f(x).
Обчислити їх у точці
,
що наближують f(x).
Обчислити їх у точці
![]() ,
що є серединою інтервалу (,).
,
що є серединою інтервалу (,).
Знайти
значення
![]() у точках
та
x1=.
у точках
та
x1=.
№ |
l |
|
|
h |
|
№ |
l |
|
|
h |
1 |
8 |
4 |
7 |
-1 |
|
16 |
6 |
1 |
4 |
6 |
2 |
6 |
3 |
5 |
2 |
|
17 |
10 |
2 |
8 |
-5 |
3 |
8 |
1 |
2 |
4 |
|
18 |
8 |
2 |
7 |
6 |
4 |
8 |
4 |
7 |
3 |
|
19 |
10 |
3 |
6 |
8 |
5 |
4 |
1 |
3 |
-2 |
|
20 |
10 |
3 |
7 |
1 |
6 |
6 |
2 |
3 |
-5 |
|
21 |
6 |
2 |
4 |
-2 |
7 |
6 |
3 |
4 |
2 |
|
22 |
8 |
1 |
4 |
2 |
8 |
10 |
2 |
8 |
-2 |
|
23 |
10 |
3 |
6 |
1 |
9 |
6 |
2 |
5 |
3 |
|
24 |
10 |
2 |
5 |
-1 |
10 |
10 |
3 |
7 |
2 |
|
25 |
8 |
3 |
4 |
2 |
11 |
6 |
3 |
4 |
-1 |
|
26 |
6 |
1 |
5 |
-3 |
12 |
4 |
1 |
3 |
-3 |
|
27 |
8 |
1 |
7 |
6 |
13 |
8 |
4 |
5 |
4 |
|
28 |
10 |
2 |
6 |
1 |
14 |
10 |
4 |
6 |
-3 |
|
29 |
10 |
2 |
6 |
-1 |
15 |
8 |
1 |
4 |
3 |
|
30 |
4 |
1 |
2 |
-2 |
