1.1.2 Приклади розв’язування задач

1. Визначити масу молекули водню.

Розв’язання:

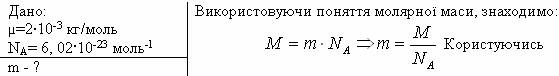
таблицею Менделєєва, знайдемо молярну масу водню:

Підставивши числові значення, матимемо:

Відповідь: m=3,35·10^-27кг.

2.  В озеро, яке має середню глибину 10м і площу поверхні 20 км², кинули кристалик кухонної солі масою 0,01г. Скільки молекул цієї солі було у наперснику води об’ємом 2 см³, взятій з озера, якщо вважати, що сіль, розчинившись, рівномірно розподілилась у всьому об’ємі води?

Розв’язання:

Кількість молекул солі в озері:

Отже,

Відповідь: N_H = 10⁶.

1.1.3. Задачі для самостійного розв’язування

1. Визначити кількість речовини і кількість молекул, що містяться в 1кг вуглекислого газу. Відповідь: v =22,7 моль, N=1,4·10²⁵.

2. На виріб, площа поверхні якого становить 20 см², нанесли шар срібла завтовшки 1 мкм. Скільки атомів срібла міститься в покритті? Відповідь: N=1,4·10²².

3. Вважаючи, що діаметр молекул водню становить близько 2,3·10^-10м, підрахувати, яку довжину мала б нитка, коли б усі молекули, що містяться в 1 мг цього газу, розташувати в один ряд щільно одна до одної. Порівняти довжину цієї нитки із середньою відстанню від Землі до Місяця (3,8·10⁵ км).

Відповідь: 6,9·10¹⁰ м, 180 разів.

4.  Густина алмазу 3500 кг/м³. Який об’єм займуть 10²² атомів цієї речовини?

Відповідь: V=5,7·10^-8м³.

5.  У скільки разів кількість атомів у 12кг вуглецю перевищує кількість молекул в 16кг кисню? Відповідь: у 2 рази. 

1.1.4. Основне рівняння молекулярно-кінетичної теорії

Ідеальним називають газ, молекули якого – матеріальні точки, між якими відсутні сили взаємодії. Молекули в такому газі співударяються за законом співударяння пружних куль. Реальні гази поводять себе як ідеальний тоді, коли середня відстань між молекулами у багато разів перевищує їхні розміри, тобто коли розрідження досить велике.Тиск у посудині з газом зумовлений ударами молекул об стінки.

p = 1/3n₀m₀v² основне рівняння МКТ -зв’язок між тиском (макроскопічним параметром) з такими мікроскопічними параметрами, як маса однієї молекули і середня квадратична швидкість руху молекул. Це рівняння можна подати й у іншому вигляді , p = 2/3n₀E отже тиск ідеального газу пропорційний середній

кінетичній енергії хаотичного руху молекул. Основне рівняння МКТ газів підтверджує той факт, що чим більші маса молекули і їхні швидкості, а також концентрація молекул, тим більший тиск вони чинять на стінки посудини.

Вводячи постійну Больцмана К = 1,38 10-²³ Дж/К, можна знайти вираз середньої кінетичної енергії поступального руху молекул через термодинамічну температуру: E = 3/2 kT-рівняння Больцмана для енергії.

Р= n₀ k T, або n₀ = -при однаковій температурі та тиску всі гази утримують в рівних об'єктах рівну кількість молекул – число Лошмідта.

N_Л - молекул в 1м³ газу при нормальних умовах:

N_l = = 2, 69 10²⁵ м^-3

1.1.5. Приклади розв’язування задач

1. Який тиск на стінки посудини створював би ідеальний газ, концентрація молекул якого 1·10²⁰м^-3, якщо їх середньоквадратична швидкість 1км/с і маса молекули 3·10^-27кг?

Розв’язання:

Відповідь:

2. Визначити середню квадратичну швидкість молекул газу, густина якого при тиску р = 50кПа становить 4,1·10^-2 кг/м³.

Розв’язання:

Добуток n₀m₀ = ρ - густина газу. Тоді р =1/3

(м/с)

Відповідь: 1910 м/с.

3. Густина газу в балоні газонаповненої електричної лампочки ρ=0,9кг/м³. Коли лампочка світиться, тиск газу в ній зростає з р₁=8·10⁴Па до р₂=1,1·10⁵Па. На скільки збільшиться при цьому середня квадратична швидкість молекул газу?

Розв’язання:

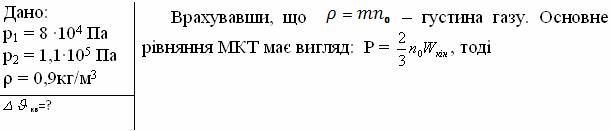
D _кв= _кв2- _кв1= 90м/с, D ( )=90м/с.

Відповідь: 90м/с.