Запитання для самоперевірки

1. Який рух називається рівномірним? Наведіть приклади.

2. Дайте означення поняття швидкості прямолінійного рівномірного руху.

3. Як на графіках зображаються шлях і швидкість рівномірного прямолінійного руху?

4. Який зв'язок між швидкістю тіла і зміною його положення під час руху?

5. Чим відрізняється миттєва швидкість у рівномірному прямолінійному русі від миттєвої швидкості в нерівномірному русі?

1. 2. Приклади розв’язування задач

Задача 1. Із пункту А до пункту В, відстань між якими l =7,5км, одночасно назустріч один одному почали рухатися два велосипедиста: перший – зі швидкістю 18км/год, другий – 9км/год. Визначити час, через який вони зустрінуться, і відстань від пункту А до місця зустрічі.

Розв’язання:

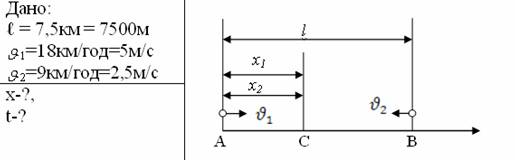
У момент зустрічі (точка С) координати велосипедистів будуть однакові. Запишемо рівняння руху велосипедистів, враховуючи, що у початковий момент (t=0) перший велосипедист знаходився на початку координат, а другий – у точці В, координату якої позначимо ?. Для велосипедиста, що рухається з пункту А: .

Для велосипедиста, що рухається з пункту В: .

В момент зустрічі , тобто.

Місце зустрічі (координата точки С): .

Підставивши числові значення, знайдемо значення величини:

Відповідь: t =1000c, x = 5км.

Задача 2. Моторний човен першу половину шляху рухався по озеру зі сталою швидкістю 36км/год, а другу – зі швидкістю 18км/год. Чому дорівнює середня швидкість моторного човна на всьому шляху?

Розв’язання:

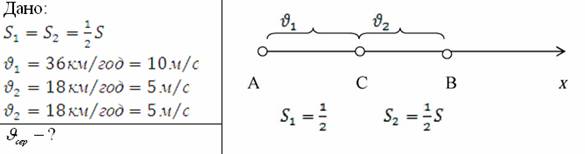
Середню швидкість човна на всьому шляху визначимо за формулою: , для першої половини - , для другої - . Підставимо значення у формулу для і, врахувавши , отримаємо: .

Зробивши обчислення, отримаємо: .

Відповідь: .

Задача 3. Моторний човен проходить відстань між двома пунктами А і В за течією річки протягом часу t₁ = 3год, а пліт – протягом часу t = 12год. Скільки часу t₂ витратить моторний човен на зворотний шлях?

Розв’язання:

рівняння (1) і (2) запишемо так:

Віднімемо від рівняння (3) подвоєне рівняння (4), дістанемо:

Звідки: , підставимо числа, отримаємо: .

Відповідь:

1. 3. Задачі для самостійного розв’язування

 Задача 1. Автомобіль проїхав першу половину шляху із швидкістю ₁ = 10м/с, а другу половину шляху – із швидкістю ₂ = 15м/с. Визначити середню швидкість на всьому шляху. Довести, що середня швидкість менша, ніж середнє арифметичне значення ₁ і ₂.

Відповідь: _с = 12м/с.

Задача 2. Тіло рухалося протягом часу t₁ = 5c зі швидкістю ₁ = 5м/с і t₂ = 10с зі швидкістю ₂ = 5 м/с і t₃ = 6с зі швидкістю ₃ = 20 м/с. Визначити середню швидкість тіла на всьому шляху.

Відповідь: _с=8,87м/с.

Задача 3. Два поїзди їдуть назустріч один одному із швидкостями 36км/год і 54км/год. Пасажир, який їде в першому поїзді, помічає, що другий поїзд проходить повз нього протягом 6с. Яка довжина другого поїзда?

Відповідь: l = 150м.

Задача 4. З двох пунктів А і В, відстань між якими дорівнює 9км, одночасно, в одному напрямі почали рухатися два мотоцикліста. Швидкість мотоцикліста, який почав рух з пункту А, - 54км/год, мотоцикліста, що виїхав з пункту В, – 36км/год. Через який час мотоцикліст, що виїхав з пункту А, наздожене мотоцикліста, що рухається з пункту В? Яке переміщення здійснить кожний мотоцикліст?

Відповідь: t = 0,5год; S₁ = 27км ; S₂=18 км.

Задача 5. Між двома пунктами, розміщеними на річці на відстані S = 100км один від одного, курсує катер, який, рухаючись за течією, проходить усю відстань за t₁ = 4 год, а проти течії – за t₂ = 10год. Визначити швидкість течії річки U і швидкість катера відносно води.

Відповідь: U=7,5км/год, =17,5км/год.

Задача 6.  Коли два тіла рівномірно рухаються назустріч один одному, то відстань між ними зменшується на S₁=16м за кожних t₁=10с. Якщо тіла з такими ж швидкостями будуть рухатися в одному напрямку, то відстань між ними буде збільшуватися на S₂=3м за кожних t₂ = 5с. Які швидкості кожного із тіл?

Відповідь: U₁=1,6м/с i U₂=0,6м/с.

Задача 7. Швидкість потягу між двома пунктами ₁ = 80км/год, середня швидкість на всьому шляху ₂ = 60км/год, час зупинки займає час t₂ = 1год. Знайти відстань між цими пунктами?

Відповідь: L=240км.