40. Тотожно істинні формули логіки предикатів
Означення. Формула логіки предикатів, яка при всіх інтерпретаціях на множині М набуває істинних значень, називається тотожно істинною на цій множині.
Означення. Формула логіки предикатів, яка тотожно істинна на довільній множині, називається тотожно істинною.
Приклад.
.
Довести
.
Будуємо
загальну інтерпретацію формули
на множині
.
Нехай
та
конкретні предикати.
.
Покажемо, що якщо ліва компонента
імплікації ( антецедент ) істинна, то
права компонента ( консеквент ) теж
істинна.
.
З означення імплікації випливає, що
,
а з цього що
.
41. Формули логіки предикатів, що не є тотожно істинними
Ознака не тотожно істинних формул. Для того щоб формула була не тотожно істинною достатньо, щоб вона хоч при одній інтерпретації приймала хибне значення.
Приклад.
.
Довести
.
Будуємо
інтерпретацію формули
.
Замінимо
конкретним предикатом
,
а
конкретним предикатом
для
.
,
Формули та є висловленнями, бо предикат в них конкретний і відсутні вільні змінні
(змінна зв’язана квантором). Використовуючи метод аналізу та синтезу, визначимо формально істинність формул та .
-
1
2
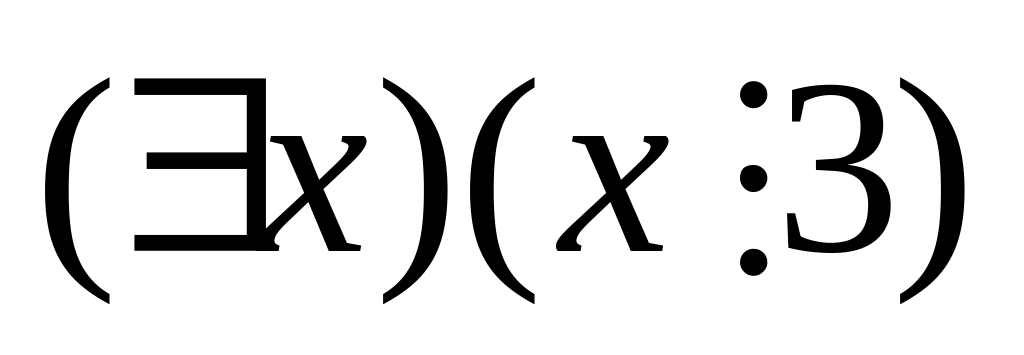
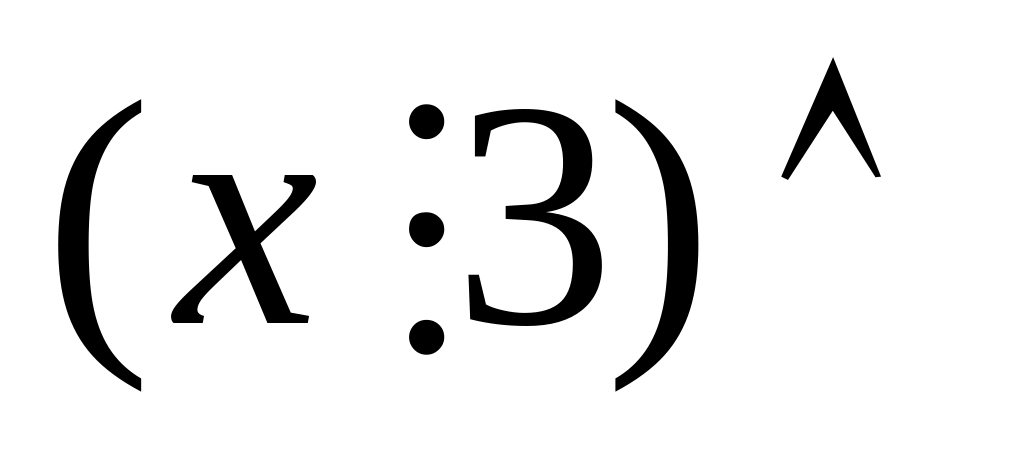
3
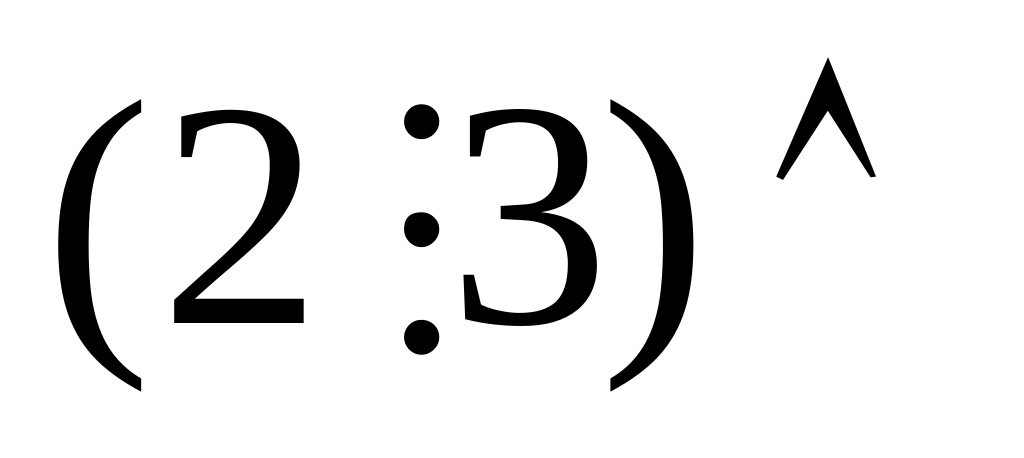
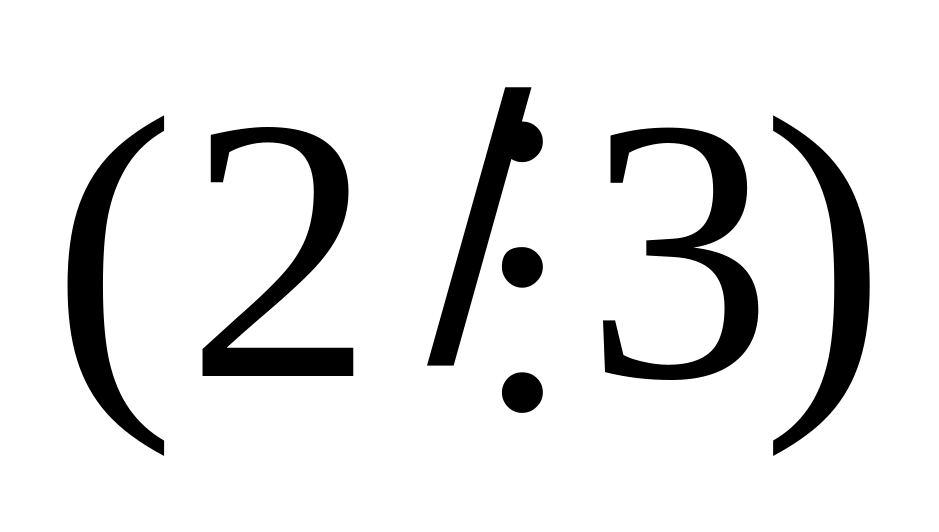
4
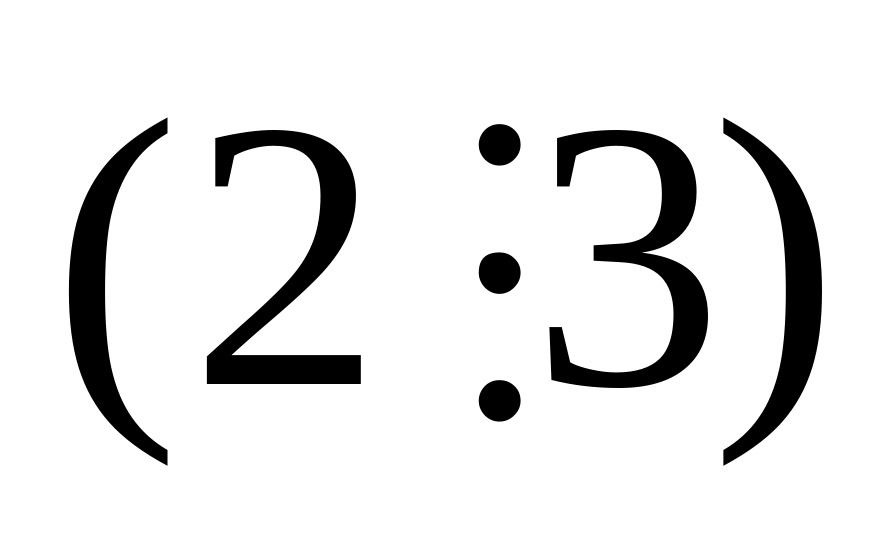
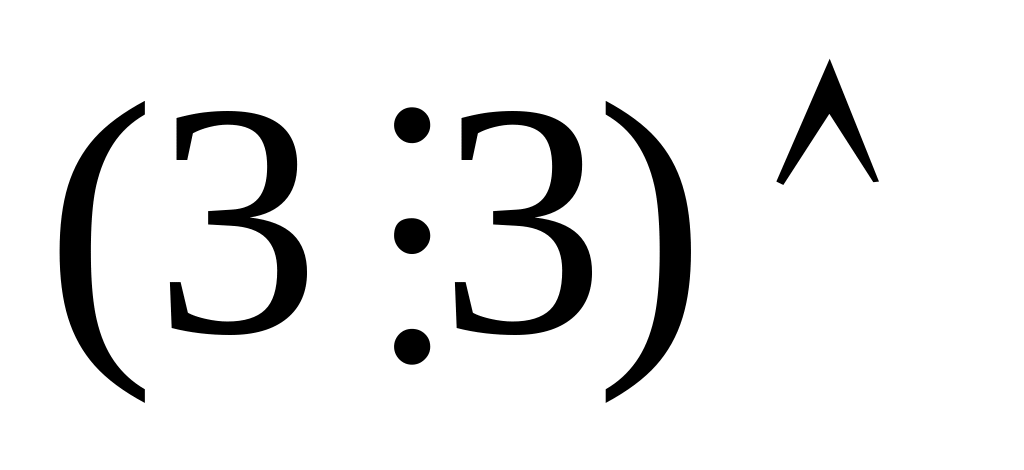
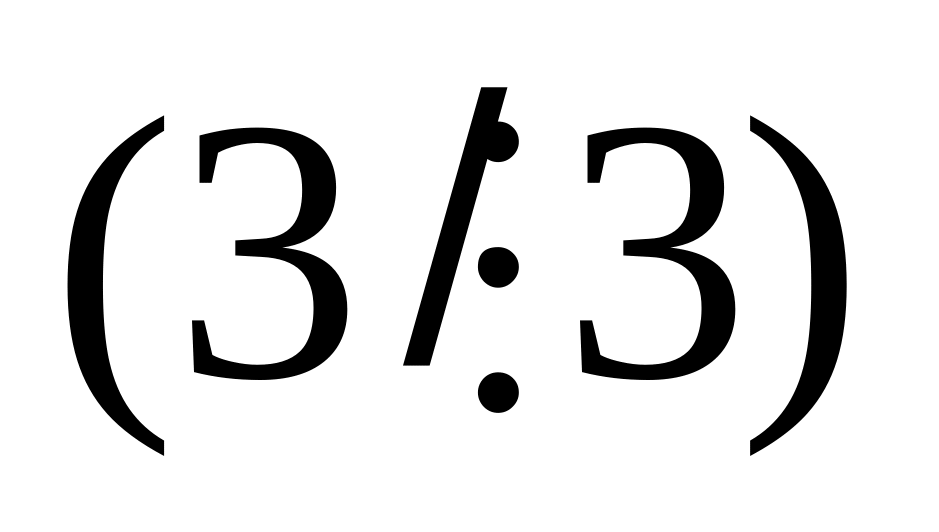
5
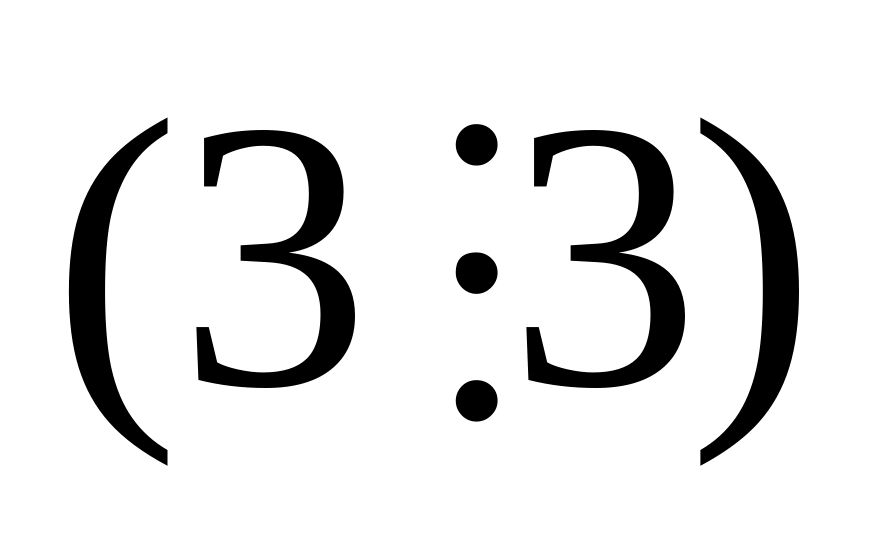
Одержали
42. Правила Де Моргана
Для
перетворення формул в логіці предикатів
часто використовують правила Де Моргана.
,
.
Доведемо
першу формулу. Нехай
,
.
Виконаємо
інтерпретацію.
,
,
де
та
конкретні предикати на довільній множині
.
Доведення:
.
Доведемо
другу формулу. Нехай
,
.
Виконаємо інтерпретацію.
,
,
де
та
конкретні предикати на довільній множині
.
Доведення:j
.
В обох випадках при довільній інтерпретації на любій множині формули та приймають однакові значення істинності. Тому вони рівносильні.
43. Зв'язок між кон'юнкцією та перетином
Нехай
деякий предикат визначений на множині
,
при цьому
,
Ø,
,
.
Множину
,
яка
є множиною істинності предиката
,
називають
характеристичною
множиною цього предиката і
позначають
.
Розглянемо
зв'язок між логічними операціями з
одномісними предикатами
,
,
та операціями теорії множин між
відповідними характеристичними множинами
цих предикатів.
Теорема.
Для
того, щоб
=
необхідно
і досить щоб
=
Необхідність. = =
Доведення.
Достатність. = =
Доведення.
Висновок. Операції кон’юнкція між одномісними предикатами відповідає операція перетин між відповідними характеристичними множинами цих предикатів.