6. Тема: Рекурсивные функции

1. Напишите рекурсивную функцию возведения в степень, пользующуюся следующим свойством: aⁿ=aa^n-1.

2. Напишите функцию возведения в степень, которая работала бы для отрицательных значений n: a^-n=1/aⁿ.

3. Напишите функцию быстрого возведения в степень, которая пользовалась бы следующими свойствами: aⁿ=(a^n/2)² при четном n, aⁿ=aa^n-1 при нечетном n.

4. Последовательность Фибоначчи определена следующим образом: φ₀=1, φ₁=1, φ_n=φ_n-1+φ_n-2

при n>1. Начало ряда Фибоначчи выглядит следующим образом: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... Напишите функцию int phi(int n), которая по данному натуральному n возвращает φ_n.

5. Для биномиальных коэффициентов (числа сочетаний из n по k) хорошо известна рекуррентная формула: C_n^k=C_n-1^k-1+C_n-1^k. Вычислите значение C_n^k пользуясь этой формулой и учитывая, что C_n⁰=C_nⁿ=1.

6. Головоломка «Ханойские башни» состоит из трех колышков, пронумерованных числами 1, 2, 3. На колышек 1 надета пирамидка из n дисков различного диаметра в порядке возрастания диаметра. Диски можно перекладывать с одного колышка на другой по одному, при этом диск нельзя класть на диск меньшего диаметра. Необходимо переложить всю пирамидку с колышка 1 на колышек 2 за минимальное число перекладываний.

Напишите программу, которая решает головоломку – для данного числа дисков n печатает последовательность перекладываний в формате «Диск 1 переложить с колышка 1 на колышек 2». Диски пронумерованы числами от 1 до n в порядке возрастания диаметров.

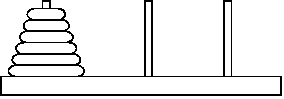
Указание: подумайте, как переложить пирамидку из одного диска? Из двух дисков? Из трех дисков ? Из четырех дисков? Напишите функцию void move (int n, int x, int y), которая перекладывает пирамидку высоты n с колышка номер x на колышек номер y.

7. Тема: Некоторые полезные алгоритмы (на применение инструкций управления циклом break и continue)

1. (Разложение на простые множители) Напишите программу, которая по данному натуральному числу n печатает все его простые натуральные делители с учетом кратности, то есть при вводе числа 132 программа должна вывести 2 2 3 11. Время работы программы должно быть пропорционально корню из n.

2. (Алгоритм Евклида) По данным натуральным числам n и m найдите их наибольший общий делитель. Количество действий должно быть порядка log max (n;m). Указание. НОД(n,m)=НОД(n mod m,m).

3. (Бинарный алгоритм Евклида) В обычном алгоритме Евклида используются остатки от деления двух чисел. Данная операция выполняется довольно медленно. В бинарном алгоритме Евклида вместо обычных делений используются только деления числа на 2. Эта операция выполняется быстро, поскольку делениe числа n на 2 равносильно сдвигу двоичного представления числа n вправо на 1 бит. Бинарный алгоритм Евклида основан на следующих свойствах: НОД(n,m)=2НОД(n/2,m/2), если n и m – четные; НОД(n,m)=НОД(n/2,m), если n – четное, m – нечетное; НОД(n,m)=НОД(n-m,m), если n, m – нечетные. Реализуйте бинарный алгоритм Евклида.

4. (Машинное эпсилон - ) Действительные числа хранятся в переменных типа double с некоторой точностью, то есть хранятся не все знаки действительного числа, а определенное их количество и порядок числа. Поэтому операции над действительными числами выполняются не точно, а с некоторым приближением. Например, существует такое число ε типа double, что 1.0+ε=1.0. Наибольшее из таких чисел называется «машинной точностью» или «машинным эпсилоном». Напишите программу, определяющую машинное эпсилон.

5. (Совершенные числа) Натуральное число называется совершенным, если оно равно сумме всех своих делителей, меньших его самого. Например, 6 – совершенное число, поскольку 6=1+2+3. Вычислите первые пять совершенных чисел.

6. Теорема Лагранжа утверждает, что любое натуральное число можно представить в виде суммы четырех точных квадратов. По данному числу n найдите такое представление. Найдите наименьшее натуральное число, которое нельзя представить в виде суммы трех точных квадратов.