
- •Методичні вказівки
- •3.3 Зміст завдання 22
- •4.2 Оцінка завадостійкості й ефективності прийому
- •4.3 Зміст завдання 38
- •1 Склад курсової роботи. Вихідні дані на курсову роботу
- •1.1 Склад курсової роботи
- •1.2 Вихідні дані на курсову роботу
- •Розрахунок статистичних характеристик і параметрів інформаційного сигналу
- •2.1. Структурна схема системи передачі інформації
- •Розрахунок статистичних характеристик і параметрів інформаційного сигналу
- •2.3 Зміст завдання
- •Розрахунок характеристик і параметрів
- •3.1 Розрахунок характеристик і параметрів аналого-цифрового перетворення повідомлення
- •Характеристики і параметри сигналів дискретної модуляції
- •Зміст завдання
- •Оцінка завадостійкості й ефективності прийому сигналів дискретної модуляції
- •4.1 Характеристики і параметри вузькосмугового неперервного гаусівського каналу зв'язку
- •4.2 Оцінка завадостійкості й ефективності прийому сигналів дискретної модуляції
- •4.3 Розрахунок характеристик і параметрів цифро-аналогового перетворення сигналу (відновленого сигналу)
- •Зміст завдання
- •Додаток в. Приклад розрахунку розділу 4.
- •Додаток г.
- •Спектральної щільності
Оцінка завадостійкості й ефективності прийому сигналів дискретної модуляції
4.1 Характеристики і параметри вузькосмугового неперервного гаусівського каналу зв'язку
Модель вузькосмугового шумового гаусівського НКЗ представляють у наступному вигляді: вхідний ідеальний смуговий фільтр (ПФ), лінія зв'язку без втрат з адитивною гаусівською рівномірно розподіленою по спектру завадою, вихідний ідеальний ПФ. Центральні частоти ПФ співпадають з частотою несучого коливання (переносника). Полоса пропускання ПФ співпадає з шириною спектра сигналу дискретної модуляції. В полосі пропускання коефіцієнт передачі ПФ приймемо рівним одиниці.
Заваду
з рівномірним спектром називають білим
гаусівським шумом БГШ.
Спектр
щільності
цього шуму
визначається як
 ,
,
 .
.
Потужність
БГШ
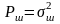 в
смузі пропускання ПФ геометрично
визначається як площа прямокутника з
висотою
G0
і
основою
Δfs
:
в
смузі пропускання ПФ геометрично
визначається як площа прямокутника з
висотою
G0
і
основою
Δfs
:
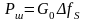 , (37)
, (37)
де Δfs визначають із співвідношень (30), (33) або (36), в залежності від виду модуляції.
Враховуючи
(37)
і
те, що потрібне відношення сигнал/шум
(ВСШ)
 на вході детектора приймача відоме,
знаходимо потужність сигналу дискретної
модуляції, що забезпечує це ВСШ:
на вході детектора приймача відоме,
знаходимо потужність сигналу дискретної
модуляції, що забезпечує це ВСШ:
 . (38)
. (38)
На
протязі посилки сигнал дискретної
модуляції має вигляд гармонійного
коливання (рисунок 4).
Потужність
гармонійного коливання в цьому випадку
дорівнює
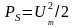 (це потужність, яка виділяється на опір
1
Ом).
Враховуючи специфіку формування сигналів
ДАМ, ДЧМ і ДФМ, одержуємо співвідношення
для їх потужності й амплітуди, які в
середньому припадають на один двійковий
символ модулюючого сигналу:
(це потужність, яка виділяється на опір
1
Ом).
Враховуючи специфіку формування сигналів
ДАМ, ДЧМ і ДФМ, одержуємо співвідношення
для їх потужності й амплітуди, які в
середньому припадають на один двійковий
символ модулюючого сигналу:
 , (39)
, (39)
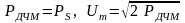 , (40)
, (40)
 . (41)
. (41)
Пропускна здібність НКЗ характеризує максимально можливу швидкість передачі інформації по даному каналу. Максимум знаходять для всіх можливих розподілень імовірностей сигналів, підведених на вхід НКЗ.
В теорії електрозв'язку доведено, що максимальна швидкість передачі інформації по НКЗ буде забезпечена шляхом застосування таких методів кодування і модуляції, які приводять до формування сигналу в ПРД з гаусівським розподілом миттєвих значень. При такому сигналі пропускна спроможність гаусівського НКЗ має вигляд:
 . (42)
. (42)
В
тому випадку, коли сигнал на вході НКЗ
відсутній, в ньому діє тільки широкосмуговий
гаусівський шум в смузі меньшій Δfш.
При дії цього шуму на смуговий фільтр
відгук останнього являє собою шум в
смузі частот
 .
Якщо
відношення
.
Якщо
відношення
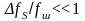 ,
то такий фільтр і, відповідно, шум на
його виході називають вузькосмуговим.
,
то такий фільтр і, відповідно, шум на
його виході називають вузькосмуговим.
Часто вузькосмугову гаусівську заваду представляють у вигляді високочастотного гармонійного коливання, модульованого по амплітуді і фазі. Можна використати дві форми такого представлення:
 ,
,
де
 ,
,
 ,
,
 ,
,
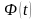 -
низькочастотні
випадкові процеси, зв'язані
співвідношеннями:
-
низькочастотні
випадкові процеси, зв'язані
співвідношеннями:
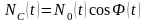 ,
,
 ,
,
 ,
,
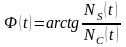 ,
,
де , - амплітуди синфазної і квадратурної складових перешкоди N(t).
Функції
щільності ймовірності (ФЩВ) миттєвих
значень
 ,
,
мають
вигляд гаусівського розподілення (1)
з
числовими характеристиками:
,
,
мають
вигляд гаусівського розподілення (1)
з
числовими характеристиками:

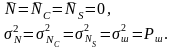
Огинаюча (змінна за випадковим законом амплітуда) гаусівської перешкоди розподілена за законом Релея, а саме:
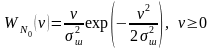 . (43)
. (43)
Миттєве значення інформаційного сигналу має вигляд:
 .
.
В разі, коли в НКЗ діє адитивна суміш гармонійного сигналу і вузькосмугової гаусівської перешкоди, впливаючої на детектор, прийнятий сигнал має вигляд:
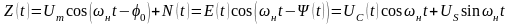 ,
,
 ,
,
 .
.
Функція
щільності ймовірності миттєвих значень
Z(t)
у
випадку, коли φ0
розподілена рівномірно
 ,
має
вигляд:
,
має
вигляд:
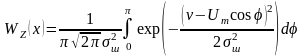 . (44)
. (44)
ФЩВ
огинаючої
 одержаного
сигналу підлягає узагальненому закону
Релея (розподіленню Райса):
одержаного
сигналу підлягає узагальненому закону
Релея (розподіленню Райса):
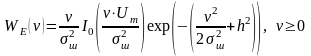 , (45)
, (45)
де
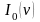 - модифікована функція
Бесселя
першого роду нульового порядку.
- модифікована функція
Бесселя
першого роду нульового порядку.
Графики
ФЩВ,
які
визначаються
співвідношеннями
(43) – (45), зображені
на рис. 5 а, б для різноманітних
значень
ВСШ
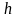 .
.
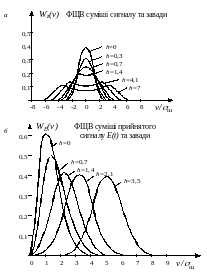
Рис. 5. Графіки ФЩВ для різних значень ВСШ
