2. Характеристики і параметри сигналів дискретної модуляції

Двійкові кодові символи цифрового сигналу (ІКМ) можуть бути передані за допомогою різних видів дискретної модуляції (маніпуляції) параметрів переносника. Так, на рисунку 4 показано: вихідний модулюючий сигнал повідомлення 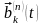, а також цифровий сигнал (рисунок 4а) і модулюючий сигнал 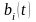у вигляді двополярних імпульсів, зв'язаних з вихідним повідомленням простим співвідношенням 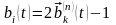(рисунок 46). На рисунку 4в зображено гармонійний переносник виду 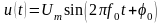, де 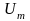– амплітуда, – частота, 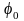– начальна фаза (далі приймемо ).

Сигнали дискретної амплітудної модуляції (ДАМ), дискретної частотної (ДЧМ) і дискретної фазової (ДФМ) модуляції показані відповідно на рисунку 4г, д, е. Модулюючий сигнал повідомлення у вигляді імпульсів відносного коду 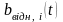, необхідний для формування сигналу дискретної відносної фазової модуляції (ДВФМ), показаний на рисунку 4ж (сам сигнал ДВФМ зображено на рисунку 4з). При цьому імпульси відносного коду формуються за правилом 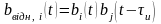, де – затриманий на тривалість посилки сигнал повідомлення , причому .

Розглянемо аналітичні подання сигналів дискретної модуляції (маніпуляції) та їх спектрів. З цією метою як модель маніпулюючого сигналу повідомлення візьмемо сигнал виду:

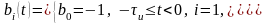(26)

Припускаючи, що сигнал повідомлення періодичний з періодом , покажемо його тригонометричним рядом Фур'є (без врахування фазових зсувів):

. (27)

З (27) виходить, що цей сигнал має тільки непарні гармонійні (спектральні) складові на частотах , .

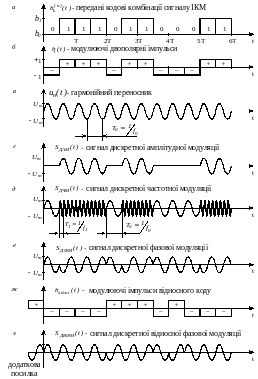
Рис. 4. Сигнали при дискретній модуляції

Сигнал ДАМ має вигляд:

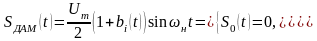(28)

Підставляючи (27) у (28), одержуємо спектральний розклад сигналу ДАМ:

. (29)

Ширина спектра сигналу ДАМ в два рази більше ширини спектра модулюючого сигналу повідомлення (цифрового сигналу):

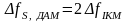. (30)

Сигнал ДЧМ представляється у вигляді

(31)

де 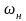– частота переносника, ;

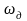– девіація частоти (максимальне відхилення частоти);

, , .

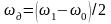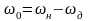Після ряду перетворень розклад сигналу ДЧМ на гармонійні складові приймає вигляд:

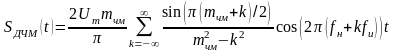, (32)

де 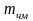– індекс частотної модуляції,

.

Із задовільною для практичних розрахунків точністю ширина спектра сигналу ДЧМ може бути визначена як:

. (33)

Сигнал ДФМ представляється у вигляді

(34)

де – індекс фазової модуляції (максимальне відхилення фази сигналу ДФМ від фази несучої).

Розклад сигналу ДФМ на гармонійні складові має наступний вигляд:

. (35)

Ширина спектра сигналу ДФМ може бути визначена наступним чином:

. (36)

Використовуючи (29), (32) і (35), будують амплітудні спектри сигналів дискретної модуляції на поверхні - амплітуда гармонійної складової - частота (МГц). Спектр сигналу ДВФМ аналогічний спектру сигнала ДФМ.

2. Зміст завдання

1. Розрахувати частоту f_д й інтервал Т_д часової дискретизації відгуку ФНЧ.

2. Розрахувати інтервал квантування Δq, пороги h_n та рівні х_n квантування квантівника АЦП.

3. Побудувати отриману характеристику квантівника х_n(h_n).

4. Розрахувати СКП квантування ξ_g² та потужність квантованого процесу Р_у.

5. Розрахувати та побудувати графіки розподілення імовірностей Р_п й інтегральне розподілення імовірності F_п.

6. Розрахувати ентропію Н_у, продуктивність Н’_у, надлишок квантування r_у квантованої послідовності (в розрахунках прийняти квантування з рівномірним кроком) та максимальну ентропію Н_тах.

7. Закодувати L-ічну послідовність двійковим безнадлишковим кодом . Виписати всі кодові комбінації коду і побудувати таблицю кодових відстаней .

8. Розрахувати ширину спектру ІКМ-сигналу .

9. Розрахувати ширину спектра Δf ІКМ сигналу.

10. Розрахувати і побудувати спектр сигналу дискретної модуляції і визначити його ширину Δf_S.

11. Зобразити функціональну схему маніпулятора і часові діаграми сигналів за заданою інформаційною послідовністю.

Усі розрахунки та побудову графіків необхідно проводити за допомогою програми "Mathcad".

Приклад розрахунку розділу показаний у додатку Б.