2. Розрахунок характеристик і параметрів

АЦП - СИГНАЛУ ТА СИГНАЛУ ДИСКРЕТНОЇ МОДУЛЯЦІЇ.

3.1 Розрахунок характеристик і параметрів аналого-цифрового перетворення повідомлення

Аналого-цифрове перетворення (АЦП) вхідного інформаційного сигналу здійснюється у три етапи. Спочатку неперервний сигнал дискретизують за часом, далі квантують за рівнем, і потім квантовані рівні кодують, в результаті чого формується цифровий сигнал. Всі ці перетворення ілюструються графічно на рисунку 2.

Теоретичною основою дискретизації є теорема В. О. Котельникова [2], відповідно до якої кожна неперервна функція x(t), що обмежена по спектру верхньою частотою f_в, може бути представлена із задовільною точністю й послідовністю своїх відліків , узятих в моменти часу 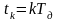і кратних інтервалу дискретизації:

. (7)

Згідно з умовами завдання відгук x(t) ідеального ФНЧ задовольняє дану теорему. Тому його можна продискретизувати, а саме, перетворити з аналогової форми x(t) в дискретно-аналогову з частотою дискретизації:

. (8)

Дискретизатор можливо реалізувати у вигляді перемножувача двох функцій: неперервного повідомлення x(t) і періодичної послідовності дискретизуючих імпульсів 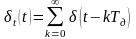(рис. 2а).

При цьому, відгук дискретизатора має вигляд , зображений на рисунку 2б (заштрихована послідовність імпульсів). Тривалість дискретизуючих імпульсів 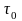значно менша інтервалу (періоду) Т_д дискретизації, і тому часто змінами амплітуди імпульсів в інтервалі тривалістю зневажають.

У момента імпульси на виході дискретизатора можуть приймати безліч значень з обмеженого або необмеженого діапазону , який називається шкалою дискретизованого сигналу. В результаті рівномірного квантування з кроком цей діапазон розбивається на кінцеву кількість рівнів квантування , . На рисунку 2в показана процедура квантування для L=4.

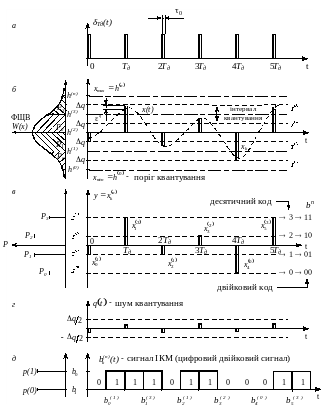
Рис. 2. Аналого-цифрове перетворення інформаційного сигналу

Для визначення кроку квантування і порогів квантування , врахуємо, що з імовірністю 0,997 гаусівський випадковий процес знаходиться в діапазоні . Якщо у цьому діапазоні розмістити L-2 рівня, а два рівні відвести на галузі за межами цього діапазону, а саме та , то крок квантування можна розрахувати за формулою 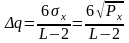(9).

. (9)

Пороги квантування можна знайти за формулою 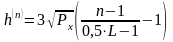(10).

, , (10)

де крайні пороги відповідно дорівнюють , ..

Рівні квантування у простішому вигляді визначаються наступними співвідношеннями:

(11)

Таким чином, правило квантування відліків полягає в наступному. Якщо вхідний відлік потрапляє в інтервал , то відгук квантівника приймає значення (рисунок 2б). Характеристика квантівника для L=4 наведена на рисунку 3.

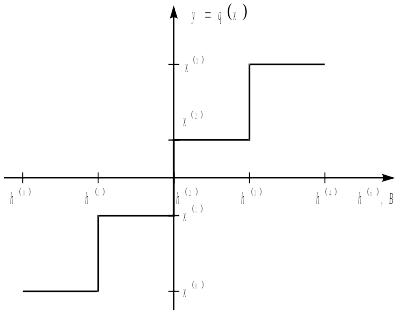
Рис. 3. Характеристика квантівника для L=4

В процесі квантування виникає специфічна погрішність 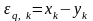, яка називається шумом квантування.

Розрахуємо - середньоквадратичну похибку квантування (СКПК) (інакше потужність шуму квантування) в моменти часу , рахуючи що .

, (12)

де – потужність перемінної складової (дисперсії) вхідного сигналу;

– потужність перемінної складової (дисперсії) вихідного сигналу;

– коефіцієнт взаємної кореляції між вхідним і вихідним сигналами.

Коефіцієнт взаємної кореляції для гаусівського процесу 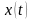знаходят як:

, (13)

де постійна К дорівнює

. (14)

У цьому співвідношенні

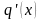- це похідна від характеристики квантування 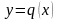(рисунок 3);

W_x(x) – ФЩВ гаусівської величини , яка визначається співвідношенням (1) 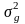на .

Підставляючи (14) в (13), а потім в (12), остаточно для СКП квантування маємо:

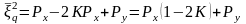, (15)

де – потужність квантованого процесу дорівнює

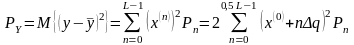. (16)

У даному співвідношенні розподілення імовірностей , дискретної випадкової величини , з урахуванням (10) розраховують як

, , (17)

де Ф(v) - табульована функція Лапласа:

.

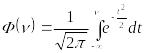Інтегральне розподілення імовірностей знаходять за формулою 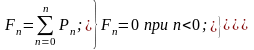(18)

(18)

Враховуючи, що відліки на виході дискретизатора некорельовані між собою, а для гаусівського процесу відповідно і незалежні, визначимо інформаційні характеристики відгуку квантівника, який є вихідним сигналом L-ічного ДКЗ. Квантована послідовність , з урахуванням незалежності її значень визначається одномірним розподіленням імовірностей з (17).

Ентропія характеризує кількісну міру невизначеності повідомлення у до його прийому, а саме ту кількість інформації, яку необхідно в середньому одержати для розпізнання будь-якого рівня з L-мірної їх множини. Ентропія визначається за формулою (19).

(19)

Продуктивність або швидкість введення інформації в ДКЗ визначається співвідношенням (20) як:

(20)

Надлишок послідовності джерела дорівнює:

, (21)

де - максимальна ентропія. Для джерела дискретних повідомлень вона буде дорівнювати:

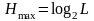. (22)

В кодері АЦП послідовність , , перетворюється в послідовність кодових символів . При організації цифрового зв'язку значне поширення знайшло двійкове кодування, коли кодові символи приймають два значення и .

Власне, процедура двійкового безнадлишкового блочного кодування відліків полягає в наступному: фізічні рівні , спочатку нумерують,а саме замінюють їх номерами 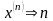, тобто представляють у вигляді десятичних цифр від 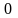до .

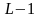Наприклад, , 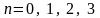(рисунок 2в). Ці десятинні числа представляють у двійковій системі лічення з основою 2 у вигляді:

, (23)

де – двійковий кодовий символ десятинного числа 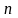, розміщеного в – й позиції кодової комбінації

, .

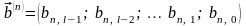Таким чином, в моменти часу 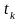рівні переводяться в числа , а останні - в кодові комбінації 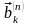, , 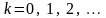. В результаті виникає цифровий сигнал. Приклад такого перетворення зображений на рисунку 2в для загальної кількості рівнів квантування L=4.

Кодову відстань Хеммінга між двома дозволеними двійковими кодовими комбінаціями 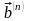та 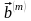визначають як кількість одиниць в їх порозрядній сумі за модулем два:

, , (24)

де – арифметична сума;

– додавання за модулем 2:

, , , .

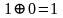Таблиця кодових відстаней будується на основі (24). При цьому - номер рядка, a - номер стовпця цієї таблиці. Оскільки вона симетрична відносно головної діагоналі, де , то доцільно виписати тільки елементи, розташовані вище головної діагоналі.

Для обчислення імовірностей 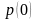та появи нуля і одиниці в сигналі ІКМ (рисунок 2д) звернемося до рисунку 2в. Ліворуч на ньому показані імовірності , , появи кодових комбінацій, а праворуч – самі кодові комбінації . Розподілення імовірностей відносно нульового рівня симетричне. Кількість одиниць і нулів в кодових комбінаціях , відповідних цим імовірностям, також симетрична.

Оскільки середня кількість нулів і середня кількість одиниць у цифровому сигналі однакова (це справедливо для гаусівського повідомлення і прийнятого способу кодування), то й імовірності їх появи також однакові .

Ширину спектра цифрового сигналу знаходять таким чином: на інтервалі дискретизації Т_д при блочному безнадлишковому кодуванні за правилом (23) повинно розміститися елементарних кодових символів. Отож їх тривалість дорівнює 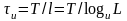, (рисунок 2д). Однак ширина спектра елементарного прямокутного імпульсу зворотно пропорційна . Таким чином, ширина спектра цифрового (ІКМ) сигналу буде дорівнювати:

, (25)

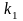де – постійна, що обирається у межах 1,5 - 2. Рекомендується обрати .