2. Розрахунок статистичних характеристик і параметрів інформаційного сигналу

За умовою завдання на курсову роботу сигнал неперервного повідомлення g(t) являє собою стаціонарний гаусівський випадковий процес з нульовим математичним сподіванням (середнім значенням) 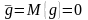, де М-знак статистичного усереднення по множині реалізацій; 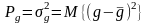- потужність; - функція кореляції, що задана в таблиці 1.

Гаусівський (нормальний) випадковій процес в будь-який момент часу характеризується одномірною функцією щільності імовірності (ФЩІ) виду 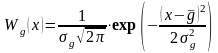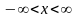[1]:

, . (1)

В часовій і спектральній областях стаціонарний процес визначається відповідно функцією кореляції і спектром щільності потужності або енергетичним спектром , де 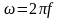. Ці характеристики пов'язані парою перетворень Вінера-Хінчина [1]:

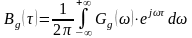; . (2)

Враховуючи те, що для стаціонарного випадкового процесу ці функції дійсні і парні, (2) можна подати у вигляді:

; . (3)

За відомими функціями 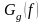і знаходять такі їх параметри, як енергетична ширина спектра й інтервал кореляції

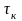
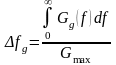; , (4)

де - максимальне значення енергетичного спектра.

Під шириною спектра розуміють ту галузь частот, в якій зосереджена основна енергія повідомлення (сигналу); під інтервалом кореляції розуміють відрізок часу між перетинами випадкового процесу, в межах якого ще спостерігається їх взаємозв'язок (кореляція); при 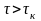цим взаємозв'язком (кореляцією) зневажають.

Вхідне повідомлення перед його аналого-цифровим перетворенням пропускається через ідеальний ФНЧ (рисунок 1).

Фільтрація - це лінійне перетворення. Тому відгук x(t) ФНЧ на гаусівський процес буде також гаусівським випадковим процесом з нульовим математичним сподіванням і потужністю, що визначається співвідношенням:

(4)

де H(f) - амплітудно-частотна характеристика АЧХ ФНЧ.

Тут ураховано, що амплітудно - частотна характеристика ідеального ФНЧ дорівнює одиниці в смузі частот [0,f_зp] і нулю за межами цієї смуги. Крім того, його смуга пропускання Δf_зр прийнята рівною ширині енергетичного спектра повідомлення Δf_3p = f_g = f_в – f_н, де f_в і f_н- відповідно верхня і нижня частоти, які за умовами домашнього завдання відповідають f_н=0,f_в>0. Звідки частота зрізу ФНЧ рівна f_зp = f_в. Це говорить про те, що відгук ФНЧ є обмеженим по спектру сигналом повідомлення. В ньому не містяться складові вхідного повідомлення на частотах f >f_в.

Кількісно втрати при фільтрації повідомлення характеризуються середньоквадратичною похибкою (СКП):

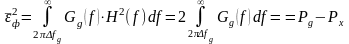. (6)

де H(f) - АЧХ реального ФНЧ.

2.3 Зміст завдання

1. Зобразити структурну схему змішаної системи зв'язку і сигнали в різних її перетинах.

2. Розрахувати та побудувати спектр щільності потужності сигналу повідомлення та функції кореляції .

3. Розрахувати енергетичну ширину спектра й інтервал кореляції сигналу повідомлення.

4. Розрахувати потужність P_х відгуку ФНЧ.

5. Розрахувати СКП фільтрації сигналу повідомлення.

Усі розрахунки та побудову графіків необхідно проводити за допомогою програми "Mathcad".

Приклад розрахунку розділу показаний у додатку А.