2.1. Вправи «небо» та «арифметика»
Вправа «небо» складається з ліній товщиною 0,1 – 0,3 мм, проведених під рейсшину (рис. 2.1.1) через 2 мм. Інтервал відкладається з боку поля вправи за допомогою вимірювача без проколювання голками паперу наскрізь, тільки з легкими відмітками.
Рис. 2.1.1 – вправа «небо» Рис. 2.1.2 – вправа «арифметика»
Вправа «арифметика» (рис. 2.1.2) являє собою «небо», доповнене лініями, проведеними під кутник, із тим же інтервалом – 2 мм. Якість цієї композиції оцінюється за розміром відхилень утворених клітинок від квадрата: чим більше відхилень, тим нижча якість цієї композиції.
Як уже відмічалось, вправи «небо» та «арифметика» можуть з'єднуватися, синтезуватися в одну з доволі складним сплетінням і комбінацією ліній.
2.2. Вправа «хвиля»
Ця композиція формується за рахунок поступових розріджень та наступних згущень ліній однієї товщини, графічно імітуючи, моделюючи хвилясту поверхню (рис. 2.2.1).
Ритм згущень і розріджень можна одержати, уявляючи фронтальну або горизонтальну проекцію хвилястої поверхні, на яку нанесені прямі лінії з рівними інтервалами (а). Це буде спрощена й дещо механічна модель хвилястості. Для більшої виразності розріджену зону зображають із більшими розрідженнями, а зону згущень ліній із більшою інтенсивністю скорочень інтервалів між ними з наступним більш інтенсивним, порівняно проекційним, зростанням інтервалів між лініями.
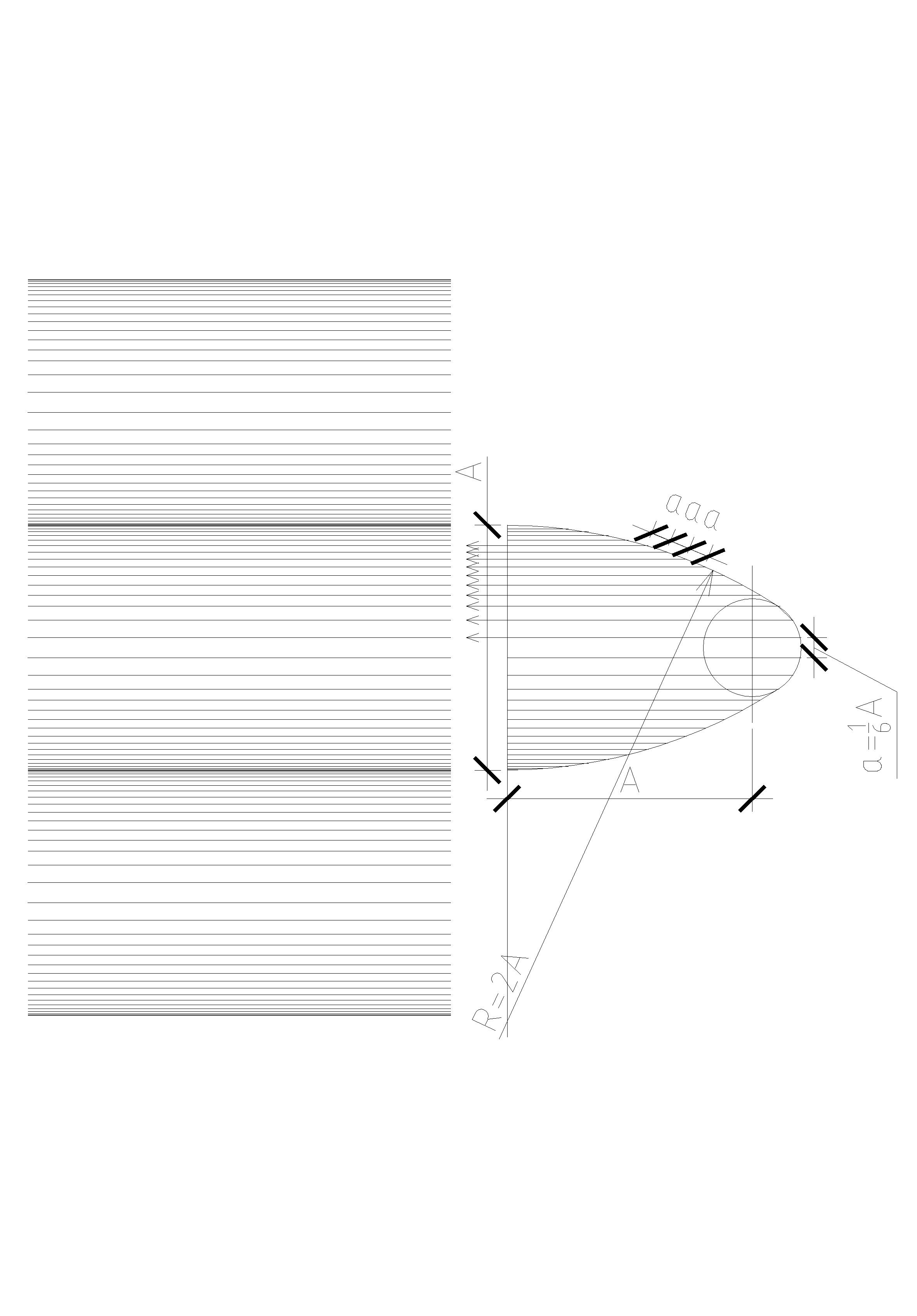
Рис. 2.2.1 – вправа «Хвиля»
2.3. Вправа «зигзаг»
Вправа «зигзаг» (рис. 2.3.1) складається з циркульних кривих, спряжених із прямими відрізками. Для утворення неперервної кривої необхідно виконати точні розрахунки членувань цієї вправи. Спочатку визначається загальний розмір вправи та прораховується радіус циркульних кривих за формулою: R= (L-an)/2b, де R – радіус внутрішнього напівкола; L – загальна довжина вправи «зигзаг»; а – кількість смуг “n” у композиції; n – загальна ширина смуги; b – кількість діаметрів напівкіл “D”, котра визначається автором. Відстань між неперервними кривими «зигзагу» дорівнює 2 – 3 мм. При виконанні композиції важливо досягти чіткості виконання спряжень та зберегти паралельність прямих відрізків.
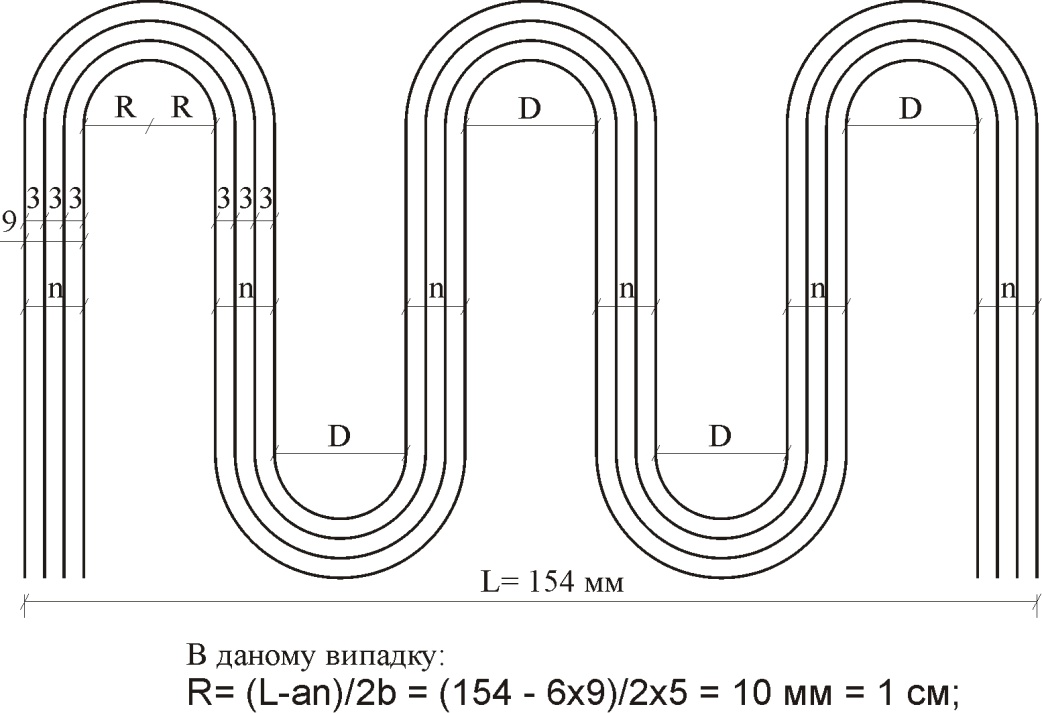
Рис. 2.3.1 – вправа «зигзаг»
2.4. Вправа «локон»
Як уже відмічалось вище, вправа «локон» і вправа «хвиля» можуть переходити одна в одну, взаємно доповнюючись, підсилюючи враження хвилястості.
Технічним (графічним) засобом моделювання хвилястої поверхні у вправі «локон» (рис. 2.4.1) є циркульні криві лінії товщиною 0,1 – 0,2 мм, одного радіуса, центри яких розміщені на одній прямій (L1 та L2) з інтервалом 2 – 3 мм. Бажано, щоб сусідні «хвилі» модельованої поверхні «локона» були «утворені» кривими різних радіусів. Це є передумовою досягнення гармонії (єдність у різноманітності).
Циркульні криві сусідніх «хвиль» повинні спрягатись. Точки спряжень кривих мають лежати на одній прямій (МN). Для досягнення чітких спряжень дуже важливо з першої кривої виконати точну побудову спряжень наступних. Для цього в ескізі намічають лінії розташувань центрів і лінії розташування точок спряжень, які повинні бути строго паралельними. Провівши похилу лінію під кутом а = 75°, визначають точки спряження «а» на лінії спряжень МN.
Розхилом циркуля Оа та О/а із центрів О й О/ проводять дуги «локона», що спрягаються у точці а. Далі виконують розбивку осі дуг через 2 – 3 мм. Із метою досягнення абсолютної ідентичності розбивки осей дуг сусідню вісь розбивають за допомогою вимірювача.
Вимірювачем дуже точно переносять поділки осі L1, від т.О/ на вісі L2. Цю операцію можна виконати також за допомогою паралельного переносу, тобто проводячи лінії, паралельно відрізку ОO/, через поділки на осі L1 ми переносимо їх на вісь L2.
Дуже важливо зберегти взаємну відповідність центрів дуг сусідніх хвиль, тобто кожному центру однієї хвилі відповідає один і тільки один центр сусідньої хвилі. Відсутність такої відповідності призведе до порушення спряжень кривих. У цьому випадку враження хвилястості не досягається.
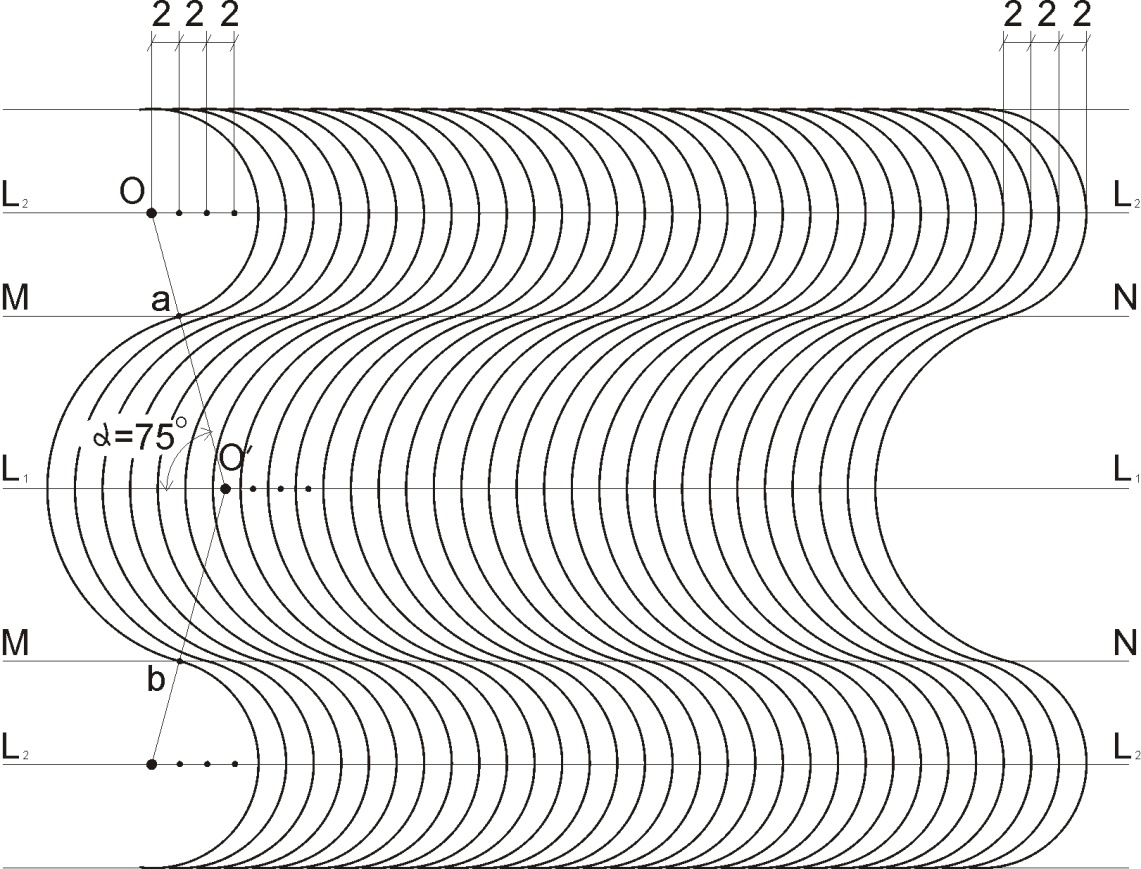
Рис. 2.4.1 – вправа «локон»