Лабораторная работа №6 Тема: Рекуррентные соотношения

Продолжительность 2 часа

Цель: овладеть методом рекуррентных соотношений при решений комбинаторных задач, уметь представлять рекуррентные соотношения в системе Mathematica 5.0.

Рекомендации студентам по подготовке к занятию: [2] Глава 5. 5. Биномиальные коэффициенты. 5.4 Разбиения

Теоретические сведения. Повторить определение рекуррентной последовательности.

Задачи: вычислять эоементы рекуррентной последовательности, решать линейные однородные рекуррентные уравнения

Порядок выполнения работы

1. Найти сотый элемент в арифметической и геометрической прогрессиях

ar[n_]:=ar[n-1]+d;

ar[1]=a0;

ar[100]

a0+99 d

gm[n_]:=gm[n-1]*q;

gm[1]=b0;

gm[100]

2. Найти двенадцатый элемент в последовательности Фибоначчи

fib[n_]:=fib[n-1]+fib[n-2];

fib[0]=fib[1]=1;

fib[12]

233

<<DiscreteMath`RSolve`

RSolve[a[n]a[n-1]+d,a[n],n]

{{a[n]d n+C[1]}}

RSolve[b[n]b[n-1]*q,b[n],n]

RSolve[[n][n-1]+[n-2],[n],n]

RSolve[{a[n]a[n-1]+d,a[0]8},a[n],n]

{{a[n]8+d n}}

RSolve[{b[n]b[n-1]*q,b[0]8},b[n],n]

RSolve[{[n][n-1]+[n-2],[0][1]1},[n],n]

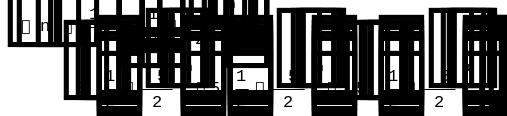
N[[12]]

N[[20]]

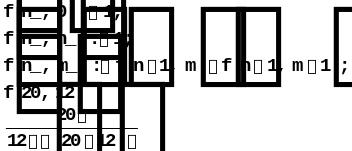
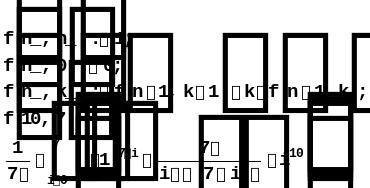
f[n_,n_]:=1;

f[n_,0]:=0;

f[n_,k_]:=f[n-1,k-1]-(n-1)*f[n-1,k];

f[10,7]

Имеются специальные встроенные функции:

StirlingS1[10,7]

StirlingS2[10,7]

Fibonacci[20]

{{x-2},{x1},{x3}}

RSolve[a[n+3]-2a[n+2]-5a[n+1]+6a[n]0,a[n],n]

RSolve[{a[n+3]-2a[n+2]-5a[n+1]+6a[n]0,a[0]-2,a[1]-14,a[2]-20},a[n],n]

Самостоятельно задание. Постройте треугольник Паскаля для биномиальных коэффициентов и аналогичные треугольники для рассмотренных последовательностей, заданных при помощи рекуррентных соотношений.

Лабораторная работа №7 Тема: Представление графов в системе Mathematica 5.0

Продолжительность 2 часа

Цель: уметь представлять неориентированные графы в системе Mathematica 5.0.

Рекомендации студентам по подготовке к занятию: [4] Глава 2. Графы. Разделы: Типы графов. Связность и маршруты.

Теоретические сведения. Неориентированный граф (граф) состоит из двух множеств – множества вершин и множества, содержащего некоторые неупорядоченные пары различных вершин, называемых ребрами.

Часто графом называют его диаграмму.

Задачи: Применение пакета дискретной математики. Построение различных известных графов. Добавление и удаление вершин и ребер.

Порядок выполнения работы

1. Открываем пакет расширения <<DiscreteMath`Combinatorica`

2. Построить полный граф с 5 вершинами

ShowGraph[CompleteGraph[5]];

3. Построить полный двудольный граф, части которого имеют 3 и 3 вершины ShowGraph[CompleteGraph[3,3]];

4. Построить «звезду» с 8 вершинами ShowGraph[Star[8]];

5. Построить «колесо» с 8 вершинами ShowGraph[Wheel[8]];

6. Пометить вершины графа

ShowGraph[CompleteGraph[5],VertexNumberTrue];

7. Присоедините к графу вершину

ShowGraph[AddVertex[CompleteGraph[5]]];

8. Присоедините к графу 3 вершины

ShowGraph[AddVertices[CompleteGraph[5],3]];

9. Постройте полный граф с 4 помеченными вершинами. Удалите вершину 1, 2, 3, 4. ShowGraph[CompleteGraph[4],VertexNumberTrue];

ShowGraph[DeleteVertex[CompleteGraph[4],1]];

ShowGraph[DeleteVertex[CompleteGraph[4],2]];

ShowGraph[DeleteVertex[CompleteGraph[4],3]];

ShowGraph[DeleteVertex[CompleteGraph[4],4]];

10. Присоедините к графу ребро

ShowGraph[AddEdge[CompleteGraph[4],{1,2}]];

11. Присоедините к графу 2 равных ребра

ShowGraph[AddEdges[CompleteGraph[4],{{1,2},{1,2}}]]

12. Присоедините к графу 2 различных ребра

ShowGraph[AddEdges[CompleteGraph[4],{{1,2},{2,3}}]]

13. Удалите 1 ребро

ShowGraph[DeleteEdge[CompleteGraph[4],{1,2}]];

14. Удалите 2 ребра

ShowGraph[DeleteEdges[CompleteGraph[4],{{1,2},{2,3}}]];

Самостоятельно задание. Используя полные графы с 1, 2, 3, 4 вершинами, присоединяя или удаляя вершины и ребра, постройте все попарно неизоморфные графы с 4 вершинами.