ЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра информатики и методики преподавания математики

Комплект учебно-методических материалов к учебной дисциплине:

Дискретная математика

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ

Для направления 230700.62 Прикладная информатика

Профиль " Прикладная информатика в образовании "

Составитель:

Вахитов Р.Х, доцент, кандидат физико-математических наук, доцент

Воронеж

200__

Используемая литература для подготовки к лабораторным работам

1. Нефедов В.Н., Осипова В.А. Курс дискретной математики. – М.: Изд-во МАИ, 1992.

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2000.

3. Носов В.А. Комбинаторика и теория графов. – М.: МГИЭиМ(ТУ),1999.

4. Харари Ф. Теория графов. – М.: Мир, 1973.

ЛАБОРАТОРНАЯ РАБОТА №1

Тема: Операции над множествами

Продолжительность 2 часа

Цель: уметь доказывать основные свойства теоретико-множественных операций.

Рекомендации студентам по подготовке к занятию: [2] Глава 1. 1.2 Операции над множествами. [3] Глава 1. §1 Множества. Отображения

Теоретические сведения. Операции на диаграммах Эйлера – Венна изображаются следующи образом:

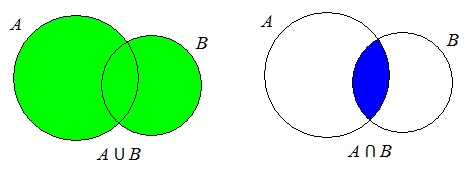
Задачи: Доказать на диаграммах Эйлера – Венна по одному из законов дистрибутивности и де Моргана.

Порядок выполнения работы

1. Докажем дистрибутивность объединения относительно пересечения:

2. Три множества A, B, C изобразим в самом общем виде, в двух копиях

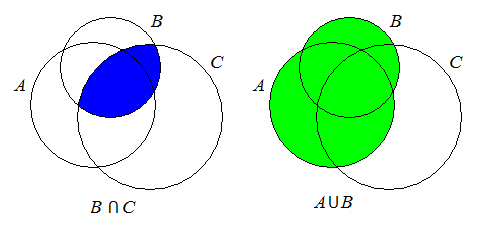
3. На первой диаграмме отметим "синее" пересечение B и C (на второй – "зеленое" объединение A и B)

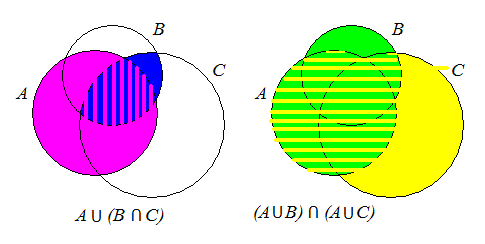
4. На первой диаграмме отметим "сиреневое" объединение A и полученного пересечения B (на второй "желтое" объединение A и С)

Самостоятельно задание. Доказать на диаграммах Эйлера – Венна по вторые из законов дистрибутивности и де Моргана. Доказать "логически": "включение слева направо" и "включение справа налево".

Лабораторная работа №2 Тема: Декартово произведение множеств. Соответствия, функции

Продолжительность 2 часа

Цель: рассмотреть свойства и графики декартовых произведений, соответствий, функций и их видов.

Рекомендации студентам по подготовке к занятию: [2] Глава 1. 1.6 Функции.

Теоретические сведения. Повторить понятия упорядоченной пары, декартова произведения, соответствия между двумя множествами, видов соответствий, функций (отображений), видов функций

Задачи: представить графики декартовых произведений точечных и непрерывных множеств, соответствий и функций в системе Mathematica 5.0

Порядок выполнения работы

1. Постройте графики АВ, ВА, АА, ВВ, если А1,2, В2,3,4

ListPlot[{{1,2},{1,3},{1,4},{2,2},{2,3},{2,4}},PlotStylePointSize[0.02],PlotRange{{-5,5},{-5,5}},AspectRatio1]

ListPlot[{{2,1},{2,2},{3,1},{3,2},{4,1},{4,2}},PlotStylePointSize[0.02],PlotRange{{-5,5},{-5,5}},AspectRatio1]

ListPlot[{{1,1},{1,2},{2,1},{2,2}},PlotStylePointSize[0.02],PlotRange{{-5,5},{-5,5}},AspectRatio1]

ListPlot[{{2,2},{2,3},{2,4},{3,2},{3,3},{3,4},{4,2},{4,3},{4,4}},PlotStylePointSize[0.02],PlotRange{{-5,5},{-5,5}},AspectRatio1]

2. Постройте графики АВ, ВА, АА, ВВ, если А[1,2], В2,3,4, выделить их синим цветом

Plot[{2,3,4},{x,1,2},PlotStyle{{Thickness[0.012],Hue[0.7]}},PlotRange{{-5,5},{-5,5}},AspectRatio1]

Show[Graphics[{Thickness[0.012],Hue[0.7],Line[{{2,1},{2,2}}],Line[{{3,1},{3,2}}],Line[{{4,1},{4,2}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

ListPlot[{{1,1},{1,2},{2,1},{2,2}},PlotStyle{PointSize[0.02],Hue[0.7]},PlotRange{{-5,5},{-5,5}},AspectRatio1]

Show[Graphics[{Thickness[0.012],Hue[0.7],Polygon[{{2,2},{2,4},{4,4},{4,2}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

3. Постройте 4 графика соотвествий из [-5,5] в [0,5]. Определите их вид: не всюду определенное и не однозначное, всюду определенное и не однозначное, не всюду определенное и однозначное, всюду определенное и однозначное (отображение множества [-5,5] на [0,5])

Plot[{2Sin[x]+2.5,2Cos[x]+2.5},{x,-3,3},PlotStyle{{Thickness[0.012],Hue[0.3]}},PlotRange{{-5,5},{0,5}},AspectRatio1,AxesTrue];

Plot[{2Sin[x]+2.5,2Cos[x]+2.5},{x,-5,5},PlotStyle{{Thickness[0.012],Hue[0.5]}},PlotRange{{-5,5},{0,5}},AspectRatio1,AxesTrue];

Plot[2Sin[3x]+2.5,{x,-3,3},PlotStyle{Thickness[0.012],Hue[0.6]},PlotRange{{-5,5},{0,5}},AspectRatio1,AxesTrue];

Plot[2Sin[3x]+2.5,{x,-5,5},PlotStyle{Thickness[0.012],Hue[0.8]},PlotRange{{-5,5},{0,5}},AspectRatio1,AxesTrue];

Самостоятельно задание. 1. Постройте графики АВ, ВА, АА, ВВ, если А[1,2][5,6], В2,3,4, выделить их красным цветом.

2. Постройте 4 графика отображений из [-5,5] в [0,5] различных видов: не сюръекции и не инъекции, сюръекции и не инъекции, не сюръекции и инъекции, сюръекции и инъекции (то есть биекции).

Лабораторная работа №3 Тема: Свойства бинарных отношений

Продолжительность 2 часа

Цель: рассмотреть важнейшие свойства бинарных отношений.

Рекомендации студентам по подготовке к занятию: [2] Глава 1. 1.5 Отношения. [3] Глава 1. §3 Бинарные отношения

Теоретические сведения.

Любое подмножество декартова квадрата M²MM множества M называется бинарным отношением P на множестве M, то есть PMM.

Бинарное отношение обычно называется отношением.

Если (x,y)P, то также пишут xPy. Отношение P на M называется:

рефлексивным, если xM xPx;

антирефлексивным, если xM xPx;

симметричным, если x,yM (xPyyPx);

асимметричным, если x,yM (xPyyPx);

антисимметричным, если x,yM ((xPyyPx)xy);

транзитивным, если x,y,zM ((xPyyPz)xPz).

связным, если x,yM (xPyyPxxy).

Задачи: представить в системе Mathematica 5.0 графики отношений, заданных на интервале [-5,5], обладающих или не обладающих одним из указанных свойств.

Порядок выполнения работы

1. Построить примеры рефлексивного, антирефлексивного и не рефлексивного и не антирефлексивного отношений

Show[Graphics[{Thickness[0.012],Hue[0.7],Polygon[{{2,2},{2,4},{4,4},{4,2}}],Line[{{-5,-5},{5,5}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.7],Polygon[{{-2,-1.9},{-2,2},{1.9,2}}],Polygon[{{-1.9,-2},{2,-2},{2,1.9}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.7],Polygon[{{-2,-1.9},{-2,2},{1.9,2}}],Polygon[{{-1.9,-2},{2,-2},{2,1.9}}],Line[{{-5,-5},{-2,-2}}],Line[{{2,2},{5,5}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

2. Построить примеры симметричного, антисимметричного, асимметричного и не симметричного и не антисимметричного отношений

Show[Graphics[{Thickness[0.012],Hue[0.],Polygon[{{-4,-2},{-4,4},{2,4}}],Polygon[{{-2,-4},{4,-4},{4,2}}],Line[{{-3,-3},{3,3}}],},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.],Polygon[{{-3,-3},{-3,-1},{-1,-1}}],Polygon[{{0,-2},{2,-2},{2,0}}],Line[{{-3,-3},{3,3}}],},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.],Polygon[{{-4,-3},{-4,-1},{-2,-1}}],Polygon[{{0,-2},{2,-2},{2,0}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.],Polygon[{{-4,-3},{-4,-1},{-2,-1}}],Polygon[{{-2,0},{-2,2},{0,2}}],Polygon[{{0,-2},{2,-2},{2,0}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

3. Построить примеры транзитивного и не транзитивного отношений

Show[Graphics[{Thickness[0.012],Hue[0.4],Polygon[{{1,1},{1,4},{3,4},{3,1}}],Line[{{0,0},{4,4}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.4],Polygon[{{1,1},{1,4},{2,4},{3,1}}],Line[{{0,0},{4,4}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

4. Построить примеры связного и не связного отношений

Show[Graphics[{Thickness[0.012],Hue[0.8],Polygon[{{-5,-5},{-5,0},{0,0}}],Polygon[{{0,0},{0,5},{5,5}}],Polygon[{{0,-5},{0,0},{5,0},{5,-5}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Show[Graphics[{Thickness[0.012],Hue[0.8],Polygon[{{-5,-5},{-5,0},{0,0}}],Polygon[{{0,0},{0,5},{5,5}}],Polygon[{{0,-5},{0,0},{5,0}}]},PlotRange{{-5,5},{-5,5}},AspectRatio1,AxesTrue]]

Самостоятельно задание.

Привести пример отношения и его графа:

а) рефлексивного, симметричного, транзитивного;

б) несимметричного, рефлексивного, транзитивного;

в) нетранзитивного, рефлексивного, симметричного;

г) нерефлексивного, симметричного, транзитивного.