5.2. Определение ударного давления и скорости распространения ударной волны

Рассмотрим гидравлический удар в трубопроводе при внезапном (мгновенном) закрытии задвижки в конце трубопровода с учетом реаль­ных условий движения жидкости, а именно: жидкость сжи­мае­ма, а стенки трубопровода обладают упругими свойствами.

За бесконечно малый промежуток времени dt после закрытия задвижки движение жидкости прекращается на расстоянииC_vdtот задвижки. На этом бесконечно малом участке трубопровода про­изойдет повышение давления на величинур(рис. 5.4).

Определим величину рс помощью закона изменения коли­чест­ва движения.

Рис. 5.4

До закрытия задвижки количество движения в рассматриваемом объеме:

, (5.1)

где –	площадь сечения трубы;
 –	плотность жидкости;
0–	скорость движения жидкости;
Сv–	скорость распространения ударной волны.

После закрытия задвижки скорость и количество движения умень­шились до нуля, т.е. в этом случае изменение количества дви­же­ния стало равно начальному количеству движения.

Это изменение количества движения должно быть равно импуль­су действующих сил.

Учитывая, что давление в сечении 1–1 равно р₀, а в сечении 2–2 повысилось дор₀ +р, находим импульс действующих сил в виде

(5.2)

Запишем закон изменения количества движения с учетом выра­же­ний (5.1) и (5.2):

.

Отсюда

. (5.3)

Формула (5.3) получена Н.Е. Жуковским и позволяет опре­де­лить повышение давления при прямом гидравлическом ударе при известной скорости распространения ударной волны C_v.

При абсолютно жестких стенках трубопровода скорость распро­странения ударной волны C_vравна скорости распространения звука в воде (C_v = 1425 м/с).

Определим скорость распространения ударной волны с учетом деформации стенок трубопровода и упругих свойств жидкости из условия сохранения массы жидкости при гидравлическом ударе.

До удара между сечениями 1–1 и 2–2 масса жидкости

. (5.4)

За время dt после закрытия задвижки в результате некоторого сжатия жидкости (т.е. увеличения ее плотности) и расширения тру­бы между сечениями 1–1 и 2–2 накопилась масса

. (5.5)

Накопленная масса образуется в трубопроводе в конце первой фазы в объеме (см. рис 5.1):

. (5.6)

Условие сохранения массы при гидравлическом ударе с учетом выражений (5.4)-(5.5) и (5.6) запишется в виде :

. (5.7)

Сокращая выражение (5.7) на dt и пренебрегая бесконечно ма­лы­ми величинами второго порядка, получим

. (5.8)

Выражение (5.8) является законом сохранения массы при гид­равлическом ударе, из которого находим скорость C_v в виде:

. (5.9)

Из выражения (5.9) видно, что скорость ударной волны зависит от де­формации трубы и сжатия , которые характеризуются уп­ру­гими свойствами материала трубы и жидкости.

Представим выражение для относительной деформации площади трубы в виде

. (5.10)

Из механики упругих тел известно, что относительная дефор­ма­ция может быть выражена в зависимости от вызываемого ею рас­тягивающего напряжения в материале трубыи модуля его упругостиE_тpпо закону Гука:

. (5.11)

Напряжение, вызванное ударной волной в стенках трубы, может быть определено по с формуле

, (5.12)

где р–	давление в гидравлическом ударе;
 –	толщина стенки трубы;
D–	диаметр трубы.

С учетом зависимостей (5.11) и (5.12) выражение (5.10) при­во­дится к виду:

. (5.13)

Относительное изменение плотности жидкости зависит от повышения давления р и модуля объемной упругости жидкости Е_ж:

. (5.14)

Подставим выражения (5.13) и (5.14) в формулу (5.9) и получим

. (5.15)

Рассмотрим физический смысл величин, находящихся под кор­нем в правой части формулы (5.15).

Если гидравлический удар, происходящий в трубе из абсолютно неупругого материала E_тр =, то

, (5.16)

где –

скорость распространения упругих деформаций (удар­ной волны) в жидкости, м/с.

Из физики известно, что выражение является скоростью звука в жидкой среде.

Для воды С_v= 1425 м/с.

В другом предельном случае при E_ж =можно считать, что гидравлический удар происходит в трубе, по которой движется абсолютно неупругая жидкость. Тогда:

. (5.17)

Можно также считать, что является скоростью распрост­ра­нения упругих деформаций (ударной волны) исключительно по те­лу трубы.

С учетом формул (5.16) и (5.17) преобразуем формулу (5.15) к виду:

(5.18)

или

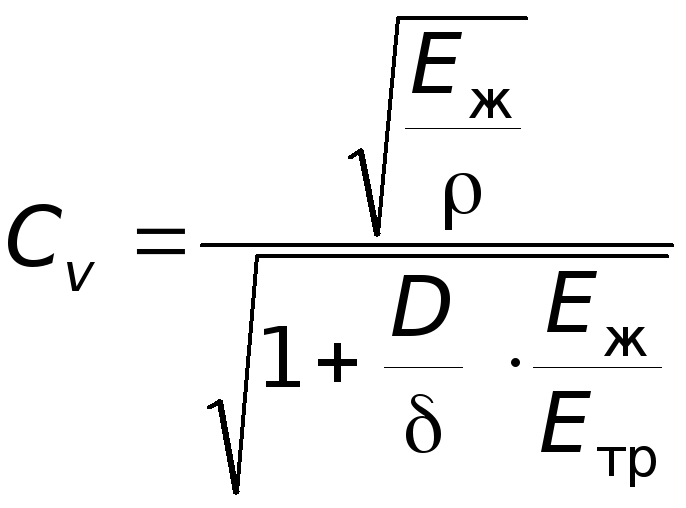. (5.19)

Учитывая, что м/с для воды, получим, м/с:

. (5.20)

Подставим выражение (5.20) в формулу (5.3) и получим, Па:

. (5.21)

Отношение для воды в зависимости от материала стенки трубы принимается по табл. 5.1.

Таблица5.1

Вид труб
Стальные	0,01
Чугунные	0,02
Асбестоцементные	0,11
Полиэтиленовые	1...1,45
Бетонные	0,10...0,14
Резиновые	333...1000

Для железобетонных труб с учетом их армирования

, (5.22)

где f–

площадь сечения кольцевой арматуры на 1 м длины стенки трубы.

Обычно .