2. Лабораторная работа №2 Тема: «Особенности применения средств измерения с различными способами нормирования пределов допускаемой основной погрешности»

Цель работы: изучение особенностей использования средств измерения (СИ) с различными способами нормирования пределов допускаемой основной погрешности.

Для выполнения лабораторной работы предварительно изучите следующие вопросы:

• какие особенности СИ определяют способ нормирования пределов допускаемой основной погрешности;

• что такое класс точности, каким условным знаком в зависимости от способа нормирования пределов допускаемой основной погрешности он обо­значается на шкале или корпусе прибора?

2.2.1. Ход работы

1. Расшифруйте условное обозначение класса точности СИ – 1,0. Изменяя значение измеряемой физической величины (ФВ) от значения до (где – пре­дел измерения или конечное значение шкалы), постройте для этого СИ гра­фики следующих зависимостей:

- абсолютной погрешности ;

- относительной погрешности ;

- точности СИ .

Анализируя графики, сформулируйте выводы по следующим вопросам:

1. Как изменяется точность СИ этого вида в зависимости от значения измеряемой ФВ?

1. Учитывая, что лабораторные приборы для измерения электрических величин выполняются, как правило, многопредельными, сформулируйте пра­вило, как следует выбирать предел измерения у приборов этого вида, чтобы точность полученных результатов была максимально возможной.

Примечание. Расшифровать условное обозначение класса точности, значит указать:

• какой вид погрешности для СИ является преобладающим;

• какая у прибора шкала;

• числовое значение какой величины указывается на шкале в качестве класса точности;

• что является нормирующим значением при нормировке предела до­пускаемой основной погрешности.

2 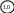. Расшифруйте условное обозначение класса точности .

Выполните все задания п.1 для СИ этого вида.

3. Расшифруйте условное обозначение класса точности .

Выполните все задания п.1 для СИ этого вида.

4 . Расшифруйте условное обозначение класса точности 1,0. Для того чтобы выяснить все особенности использования СИ этого вида, необхо­димо рассмотреть конкретное СИ. Наиболее характерным прибором, отно­сящимся к СИ этого вида, является омметр. Омметры непосредственной оценки строятся на базе микроамперметров магнитоэлектрической системы по последовательной и параллельной схемам (см. рис.2).

а)	б)

Рис. 2. Схемы построения омметра на основе микроамперметра: а – последовательная; б – параллельная

Для любой из схем величина измеренного сопротивления подклю­чается к входным зажимам омметра и преобразуется измерительной цепью прибора в изменение тока, протекающего через измерительный прибор (мик­роамперметр). Связь между величиной сопротивления и величиной тока, протекающего через микроамперметр однозначная, то есть шкала микроам­перметра может быть отградуирована в значениях измеряемого сопротивле­ния. Причем переградуировать шкалу микроамперметра можно расчетным путем.

Пусть омметры строятся на базе микроамперметра с пределом измере­ния , классом точности 1,0, имеющего шкалу прямолинейной формы со световым указателем, число делений шкалы , а геометрическая длина ее .

Для микроамперметра класса 1,0 с абсолютная погрешность, как следует из п. 1, в любой точке шкалы постоянна и равна:

,

или шкалы (т. к. шкала равномерная и ),

или шкалы (т. к. шкала имеет и разделена на 100 одинако­вых делений).

Следовательно, в рассмотренном случае можно говорить, что абсолютная погрешность прибора равна шкалы в любой точке (помня о том, что вся шкала имеет длину 100 мм, и отклонение указателя на всю шкалу соответствует току в 100 мкА)

4.1. Для омметра по последовательной схеме (см. рис. 2, а) пере­градуируйте шкалу микроамперметра расчетным путем, если известно, что , внутреннее сопротивление источника , , а выбирается из тех условий, что при (входные зажимы омметра зако­рочены) ток через микроамперметр должен соответствовать .

Обратите внимание на то, что нулевая отметка шкалы у такого омметра находится справа (на отметке, соответствующей току через прибор в ).

Для того, чтобы переградуировать шкалу расчетным путем, проделайте следующее:

1. Получите в общем виде уравнение шкалы омметра

,

где n – деления шкалы микроамперметра.

2. Оцените диапазон значений измеряемого сопротивления для данной схемы омметра, для чего воспользовавшись уравнением шкалы, полученным в п.1, определите величину для отклонения указателя на одно деление и на 99 делений шкалы микроамперметра.

2. Составьте градуировочную таблицу, выбрав в диапазоне измеряемых значений ряд точек, охватывающих всю шкалу (удобных, на ваш взгляд, для получения рабочей шкалы омметра) и рассчитав по уравнению шкалы количество делений, на которое отклонится световой указатель микроампер­метра при измерении соответствующего сопротивления.

2. В масштабе 1:1 изобразите шкалу омметра в таком виде:

Для полученного омметра абсолютная погрешность в любой точке шкалы остается также постоянной и равной ±1 мм шкалы, то есть погреш­ность аддитивная. Класс точности таким приборам присваивается по величи­не приведенной погрешности, выраженной в процентах.

В том случае, если у омметра нет опреде­ленного конечною значения измеряемой величины ( не может быть нор­мирующей величиной), а абсолютную погрешность удобно выражать в долях длины шкалы, то в качестве нормирующей величины следует выбрать геомет­рическую длину шкалы в мм. Следовательно, для полученного вами омметра

и его класс точности 1,0 . Символ внизу числового значения класса точ­ности указывает на то, что шкала у прибора резко нелинейная и нормировка предела допускаемой основной погрешности ведется относительно геомет­рической длины шкалы.

5) Выбрав ряд характерных точек на шкале омметра (не менее 10 в пре­делах всей шкалы), подсчитайте для каждой точки расчетные значения аб­солютной и относительной погрешностей и точности прибора и постройте графики:

, , .

Для определения абсолютной погрешности в единицах измеряемой ве­личины (Ом) в некоторой точке шкалы, соответствующей измеряемому сопротивлению , необходимо по градуировочной таблице (или по постро­енной шкале омметра) найти число делении , соответствующих этому со­противлению, затем рассчитать (используя уравнение шкалы) величину со­противления для точки (что соответствует верхней границе интервала неопределенности для , т. е. ) и для точки (что соот­ветствует нижней границе интервала неопределенности для , т. е. ). В большинстве случаев , т. е. границы интер­вала неопределенности для измеряемого сопротивления в единицах изме­ряемой величины получаются несимметричными (влияние резкой нелиней­ности шкалы). Для построения графиков используйте большее по модулю значение погрешности.

Сравните полученные графики с графиками, полученными в п. 1 для СИ, у которого также преобладает аддитивная погрешность, но шкала прибора линейная.

4.2. Для омметра по параллельной схеме (рис. 2, б) переградуи­руйте шкалу микроамперметра расчетным путем при тех же условиях, что и в п. 4.1. Выполните для этого омметра подпункты 1÷4 задания из п. 4.1.

Сравнив результаты, полученные в п.п. 4.1 и 4.2, сформулируйте ответы на следующие вопросы:

1) Изменится ли характер зависимостей погрешностей и точности для омметра по параллельной схеме по сравнению с теми зависимостями, кото­рые получены для последовательной схемы омметра в п. 4.1? Если такой вывод сделать затрудняетесь, выполните задание подпункта 5 из п. 4.1 для омметра по параллельной схеме.

2) В чем разница между омметрами, построенными по последовательной и параллельной схемам? Какова область применения каждой из схем?

4.3. Опишите порядок действий при определении абсолютной погрешности результата измерения в единицах измеряемой величины (Ом) любым из двух омметров при реальном использовании прибора, когда уравнение шкалы неизвестно, а имеется только шкала реального омметра и известны: отсчет по шкале для измеряемого сопротивления, класс точности омметра и длина его шкалы. Приведите конкретный пример с использованием одной из полученных вами шкал, задав отсчет по шкале для самостоятельно и считая, что класс точности омметра 2,0 , а геометрическая длина шкалы та же – 100 мм.