4.2. Позацентровий стиск

Позацентровий стиск - найпоширеніший вид силового навантаження на кам’яні конструкції (стіни, простінки, колони).

Характер напруженого стану кладки при позацентровому стиску залежить від ексцентриситету e₀ прикладання поздовжньої сили N. При незначних ексцентриситетах увесь переріз стиснутий (рис. 4.3, а). Зі збільшенням ексцентриситету епюра напружень стає двозначною, тобто переріз частково стиснутий, а частково - розтягнутий (рис. 4.3, б).

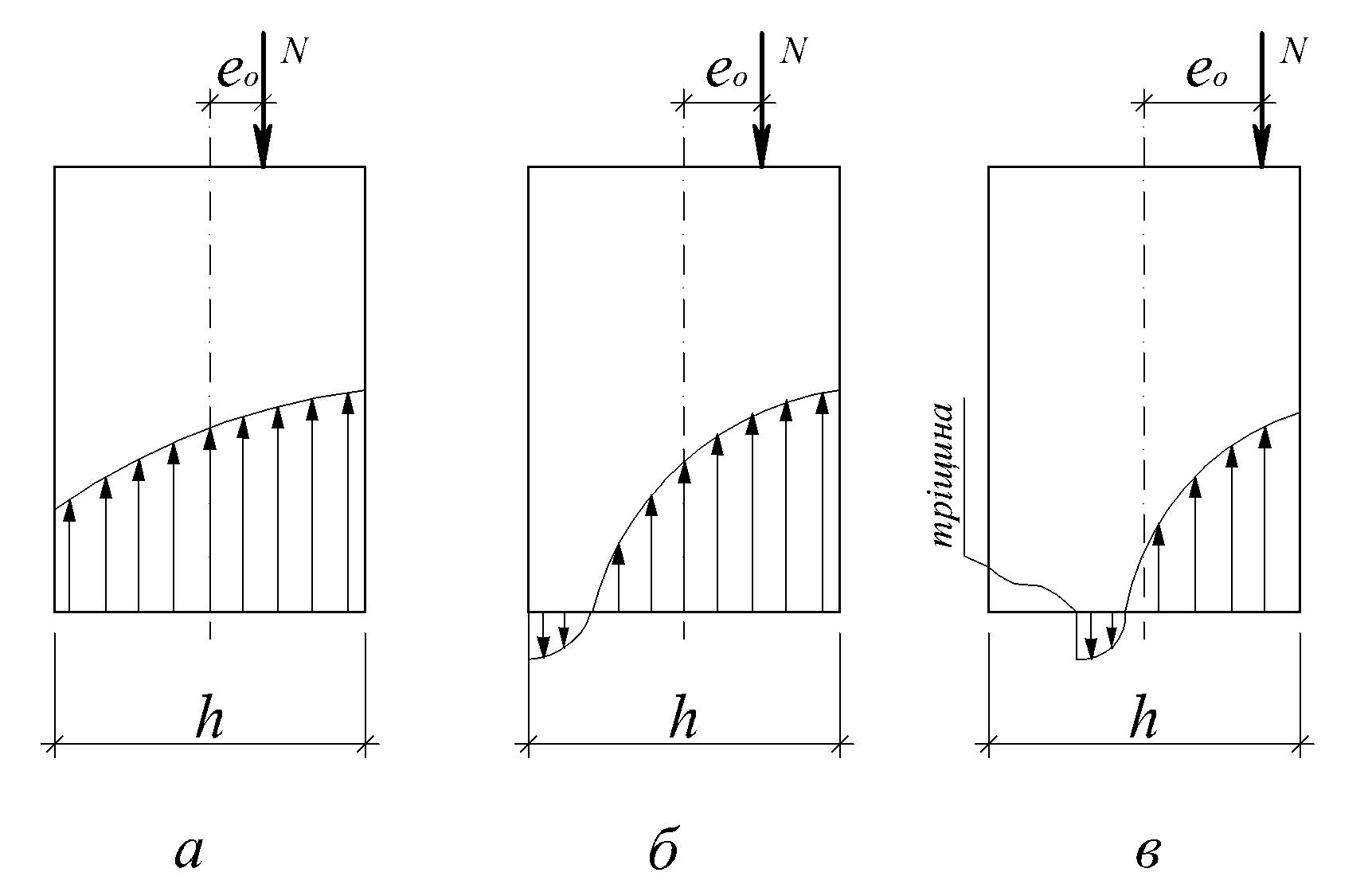
а б в

Рис. 4.3. Напруження у кладці, що працює на позацентровий стиск: а – весь переріз стиснутий; б – поява розтягу в частині перерізу; в – виникнення тріщини у розтягнутій частині перерізу

При великих ексцентриситетах, навіть при незначних навантаженнях, у розтягнутій зоні елемента напруження можуть перевищувати граничний опір кладки розтягу при згині і можуть з’явитися горизонтальні тріщини (рис. 4.3, в). Поява таких тріщин не призводить до руйнування елемента, якщо значення напруження у стиснутій зоні не більше граничного. Руйнівне навантаження може у декілька разів перевищувати навантаження, при якому утворились тріщини в розтягнутій зоні кладки.

За результатами експериментальних досліджень при розрахунку кладки на позацентровий стиск прийняті такі передумови: в основі розрахунку – умова рівноваги між зовнішньою розрахунковою силою N і прямокутною епюрою стискувальних напружень у кладці замість дійсної криволінійної епюри (рис. 4.4); розмір епюри стискувальних напружень d приймають таким, щоб центр ваги стиснутої зони А_с співпадав із точкою прикладання зовнішнього стискувального навантаження.

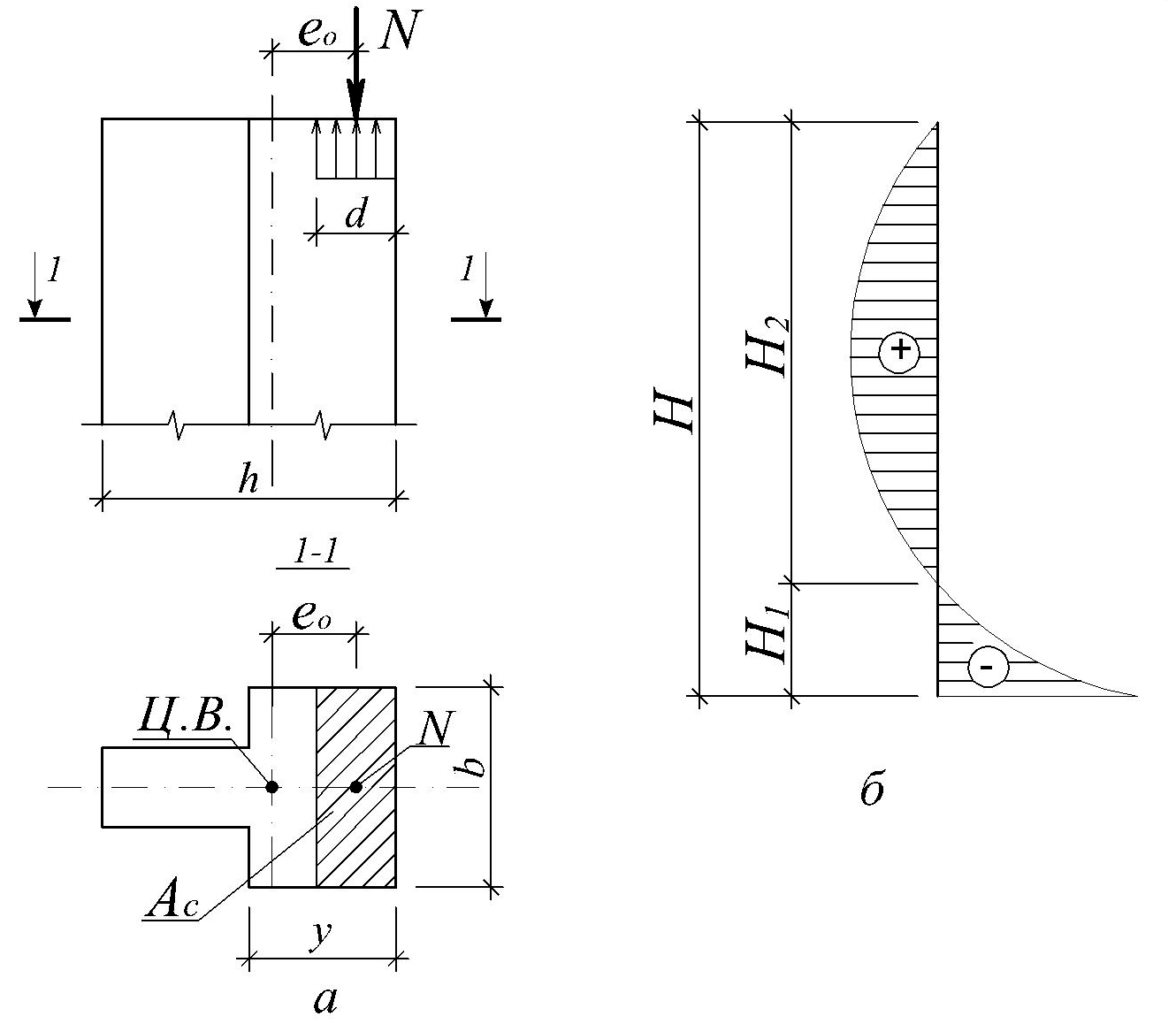
Рис. 4.4. Позацентровий стиск кам’яного елемента:

а – розрахунковий поперечний переріз; б – знакозмінна епюра

згинального моменту для позацентрово стиснутого елемента

Міцність стиснутої ділянки кладки при позацентровому стиску більша, ніж при центральному стиску. Це обумовлене стримуючим впливом оточуючої розтягнутої або потрісканої (а, отже, і незавантаженої) кладки. Причому, цей вплив тим більший, чим менша відносна висота стиснутої зони, тобто чим більший ексцентриситет.

У розрахунках підвищення розрахункового опору кладки при позацентрованому стиску враховують множенням табличного значення розрахункового опору R кладки стиску на коефіцієнт , який залежить від виду і форми перерізу кладки (табл. 4.3).

Таблиця 4.3

Визначення коефіцієнта 

Вид кладки	Переріз
	прямокутний	довільної форми
Кладка всіх видів, крім вказаних у п.2.
Кладка з каменів і крупних блоків із ніздрюватого та крупнопористого бетонів; із природних каменів, у т.ч. бутового	1	1

Примітка. Якщо 2у  h , то при обчисленнях значення коефіцієнта  замість 2у беруть h.

Розрахунок позацентрово стиснутих елементів ведуть за умови:

N  N_u .

З урахуванням гнучкості, тривалості дії навантаження і ефекту обойми рівняння для розрахунку неармованої кладки на позацентровий стиск має вигляд:

N_u = m_g1 ₁ R A_c , (4.3)

де A_c – площа стиснутої частини перерізу, для прямокутного

перерізу визначають за формулами :

A_c = вh_c; h_c = h - 2 e₀; А_с = А (1 – 2 e₀ / h), (4.4)

тут h – висота перерізу елемента у напрямку дії згинального

моменту.

Для складних типів позацентрово стиснутих перерізів положення межі стиснутої частини перерізу визначають із умови рівності нулю статичного моменту цієї частини перерізу відносно осі, яка проходить через точку прикладання стискувальної сили N.

Для таврового перерізу відстань х від точки прикладання сили до границі стиснутої зони визначають за такими формулами :

1. При ексцентриситеті у бік полиці тавра (рис. 4.5, а)

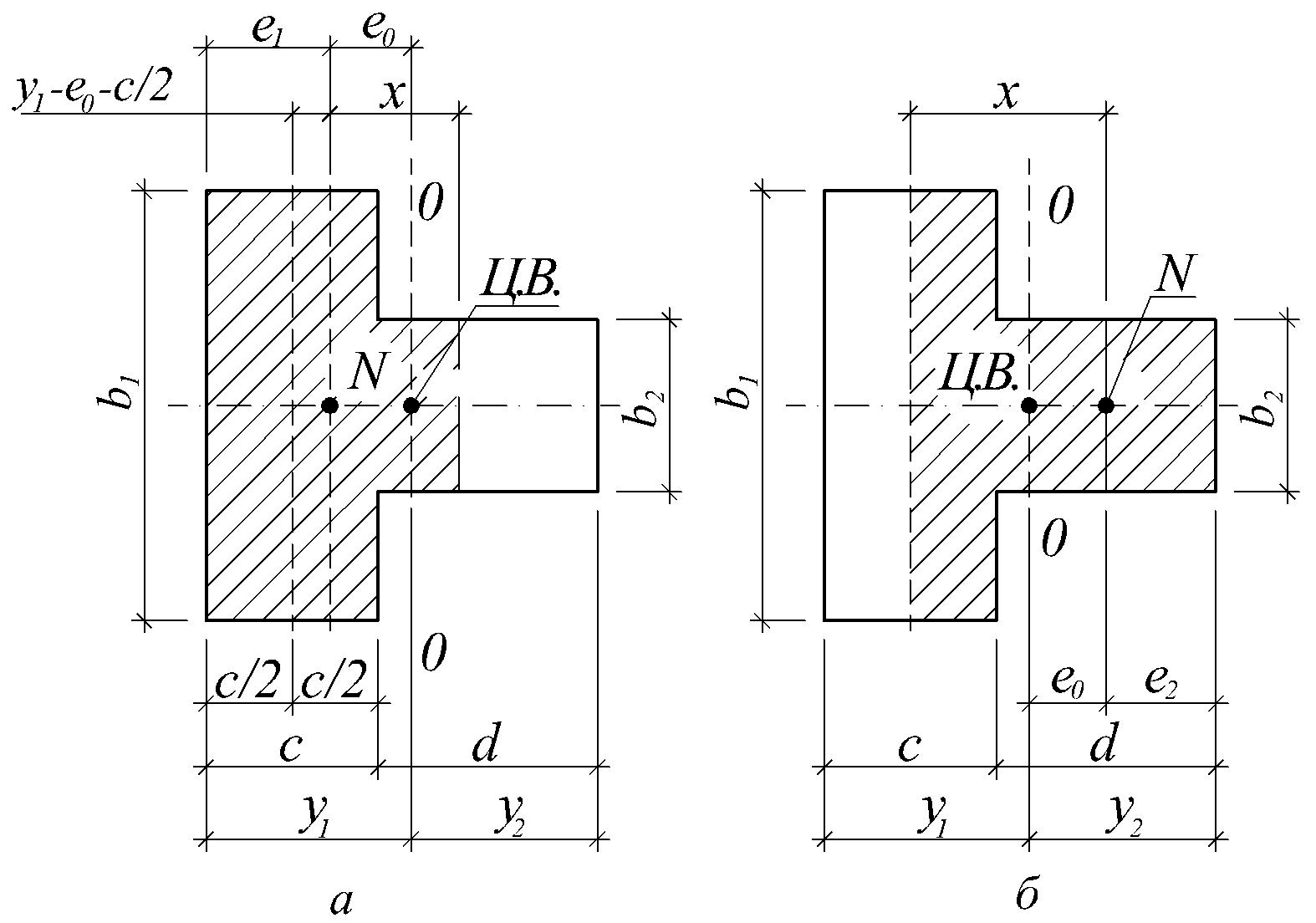
Рис. 4.5. Положення границі стиснутої зони у тавровому перерізі: а – стискувальне зусилля прикладене у

межах полиці; б – стискувальне зусилля у ребрі

а) при у робочий переріз A_c входить лише частина полиці, симетрична відносно точки прикладання сили N, тоді x = e₁ = у₁ – е_о , де e₁ – відстань від точки прикладання сили N до стиснутої грані перерізу:

; (4.5)

б) при е₁  с /2 і е₁ + x  с величину x визначають із формули:

, (4.6)

тоді . (4.7)

2. При ексцентриситеті у бік ребра тавра (рис. 4.5, б):

, (4.8)

де е₁ = y₂ – e_о ,

тоді A_c = (h – с)  b₂ + [с - ( y + e_о – x)]  b₁ . (4.9)

При е₂ ≤ d /2; x = e₂ .

Для таврового перерізу при e_о  0,45y (де y - відстань від центру ваги перерізу елемента до його краю у бік ексцентриситету), можна користуватися і спрощеними формулами:

A_c = h_c  b₂; h_c = 2 (y - e_о), (4.10)

де b – ширина стиснутої зони перерізу (ширина стиснутої

полиці або товщина стінки ребра таврового перерізу

залежно від напрямку ексцентриситету);

₁ – коефіцієнт поздовжнього згину при позацентровому

стиску, визначають за формулою:

₁ = ( + _с ) / 2 , (4.11)

 – коефіцієнт поздовжнього згину для усього перерізу

висотою h у площині дії згинального моменту,

визначають за розрахунковою висотою елемента l_о за

табл. 4.1;

_с – коефіцієнт поздовжнього згину для стиснутої зони

перерізу висотою h_с у площині дії моменту, визначають

за фактичною висотою елемента H за табл. 4.1 при

відношенні _h,c = H/ h_c або _і,c = H/ і_c ;

h_c , i_c – висота і радіус інерції стиснутої частини поперечного

перерізу в площині дії згинального моменту.

При знакозмінній епюрі згинального моменту по всій висоті стиснутого елемента розрахунок міцності ведуть у перерізах із максимальними згинальними моментами різних знаків.

У формулі (4.3): m_g1 – коефіцієнт умов роботи, що враховує вплив прогину стиснутого елемента на його несучу здатність при тривалій дії навантаження, визначають за формулою:

, (4.12)

де e_оg – ексцентриситет дії тривалих навантажень;

N_g ,  – те ж, що у (4.2).

При h  300 мм або і  87 мм коефіцієнт m_g1 = 1.

При розрахунку позацентрово стиснутих несучих і самонесучих стін завтовшки 250 мм і менше, крім розрахункового ексцентриситету дії поздовжньої сили потрібно враховувати випадковий ексцентриситет , який для несучих стін становить 20 мм, для самонесучих і окремих шарів тришарових несучих стін – 10 мм, а для перегородок і ненесучих стін, а також для заповнення фахверкових стін випадковий ексцентриситет допускається не враховувати [26, п. 4.9].

Ширина і глибина розкриття тріщин у кладці обмежені і залежать від ексцентриситету е_о, тому нормами встановлені його граничні значення:

- у позацентрово стиснутих конструкціях без поздовжньої арматури в розтягнутій зоні значення ексцентриситету (з урахуванням випадкового) не повинно перевищувати: 0,9у – для основних сполучень навантажень; 0,95у – для особливих сполучень;

- у стінах завтовшки 250 мм і менше: 0,8у - для основних сполучень навантажень; 0,85у - для особливих сполучень. При цьому відстань від лінії дії сили до краю конструкції повинна бути не меншою за 20 мм.

При e₀  0,7y позацентрово стиснуті елементи розраховують лише за міцністю. Якщо ж умова міцності не виконується, то ведуть розрахунок розтягнутої зони на розкриття тріщин.

Елементи, що працюють на позацентровий стиск, у тих випадках, коли ширина перерізу менша за її висоту (b  h), повинні перевірятись розрахунком на центральний стиск у площині, перпендикулярній до площини дії згинального моменту.