8.3. Розрахунок багатоповерхових будівель на дію вітрового навантаження

Тиск вітру, що діє на будівлю, може прикладатись під будь-яким кутом у плані. У поздовжньому напрямку просторова жорсткість будівлі значно більша, ніж у поперечному, тому вплив поздовжньої складової вітрового навантаження не є небезпечним і при розрахунку враховують лише поперечну складову, яка, залежно від напрямку вітру, змінюється від нуля до максимуму, що є сумою активного і пасивного тисків вітру, визначена згідно з [9]. Розрахунок ведуть за максимальним тиском вітру.

У будівлі вітрове навантаження послідовно сприймають поздовжні стіни, перекриття, які служать опорами для цих стін, і поперечні стіни, які є опорами для перекриттів і вертикальних діафрагм жорсткості.

Розраховують поздовжні і поперечні стіни.

У поздовжніх стінах вітрове навантаження викликає місцевий згин із площини стіни. У багатоповерхових будівлях висота поверхів значно менша від відстані між поперечними стінами, тому поздовжня стіна при розрахунку на вітрове навантаження розглядається як балкова плита, защемлена на рівні перекриття, і розраховується у короткому напрямку (рис. 8.4).

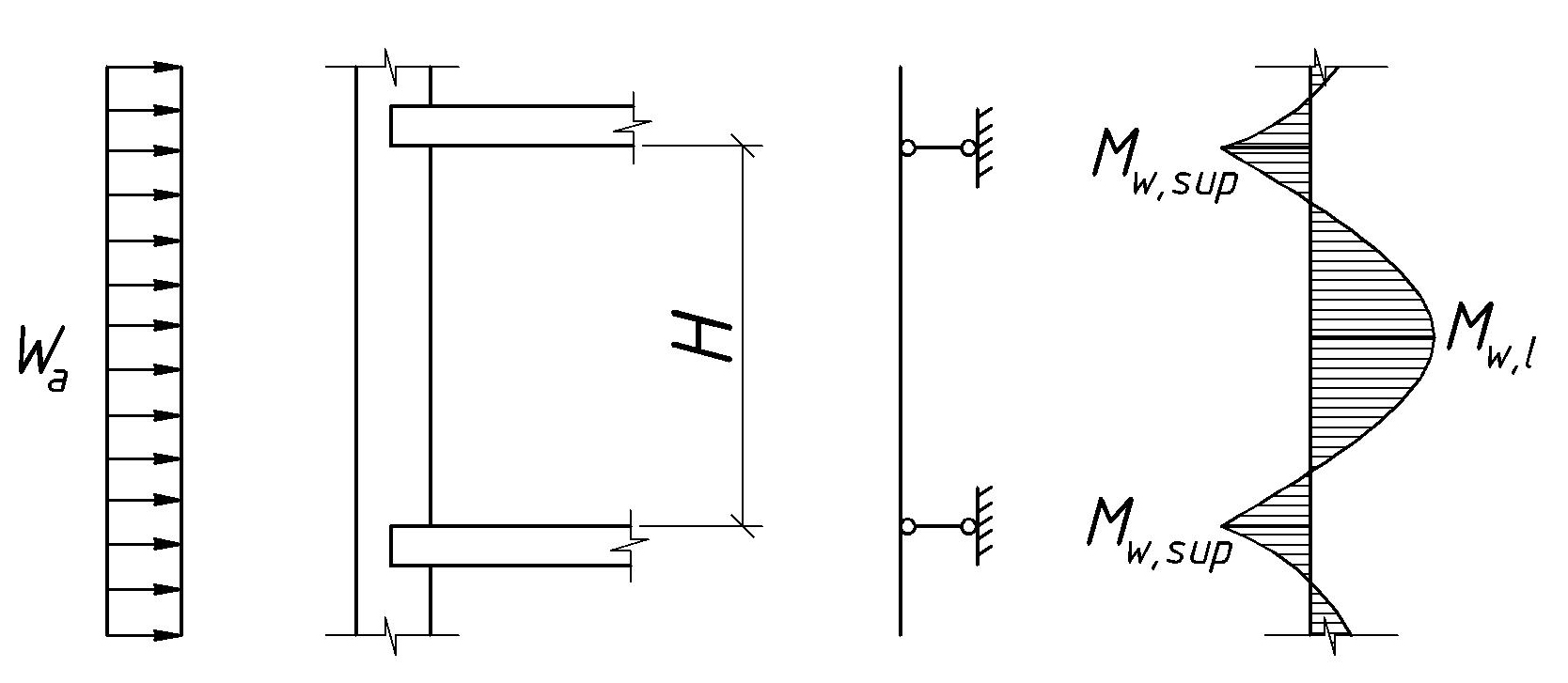
Рис. 8.4. Розрахункова схема стіни при дії місцевого

вітрового навантаження

Згинальний момент М_w,sup на рівні перекриття при активному тиску вітру додається до згинального моменту М_I від перекриття. Його значення для всіх поверхів, крім верхнього, може бути визначене, якщо припустити жорстке защемлення обох кінців і пружну роботу кладки, за формулою:

, (8.3)

де w_a - активне вітрове навантаження на 1 м висоти стіни;

H - висота поверху.

Якщо верхня опора верхнього поверху шарнірна, згинальний момент у нижньому защемленні стіни цього поверху визначають із формули:

. (8.4)

Згинальний момент від активного вітрового навантаження у середній частині висоти стіни буде гасити момент від перекриття, тому його при активному тиску вітру враховувати не потрібно.

У цьому перерізі додатковим буде згинальний момент від пасивного вітрового навантаження w_p , він становить

. (8.5)

Проте ця величина порівняно незначна. Висота поверхів житлових і громадських будівель невелика, значення М_w,l набагато менше за М, тому при розрахунку поздовжніх стін місцеве вітрове навантаження можна не враховувати.

Для розрахунку поперечних стін встановлюють, що рівнодійна вітрового навантаження W розподіляється між окремими стінами залежно від їх розмірів і положення у плані. При проектуванні доцільно поперечні стіни розташовувати симетрично для спрощення розрахунків, оскільки вітрове навантаження розподілятиметься між ними пропорційно до їх жорсткості.

При розрахунку поперечні стіни вважають вертикальними консолями, защемленими в основі, які працюють під впливом тиску вітру на згин. Переріз цих консолей приймають залежно від з’єднання між поперечними та поздовжніми стінами. У кам’яних масивних стінах це спряження забезпечене перев’язкою швів і є жорстким, тому переріз консолей буде мати форму двотавра або швелера (рис. 8.5), ребром якого є поперечна стіна, а полицями – ділянки поздовжніх стін.

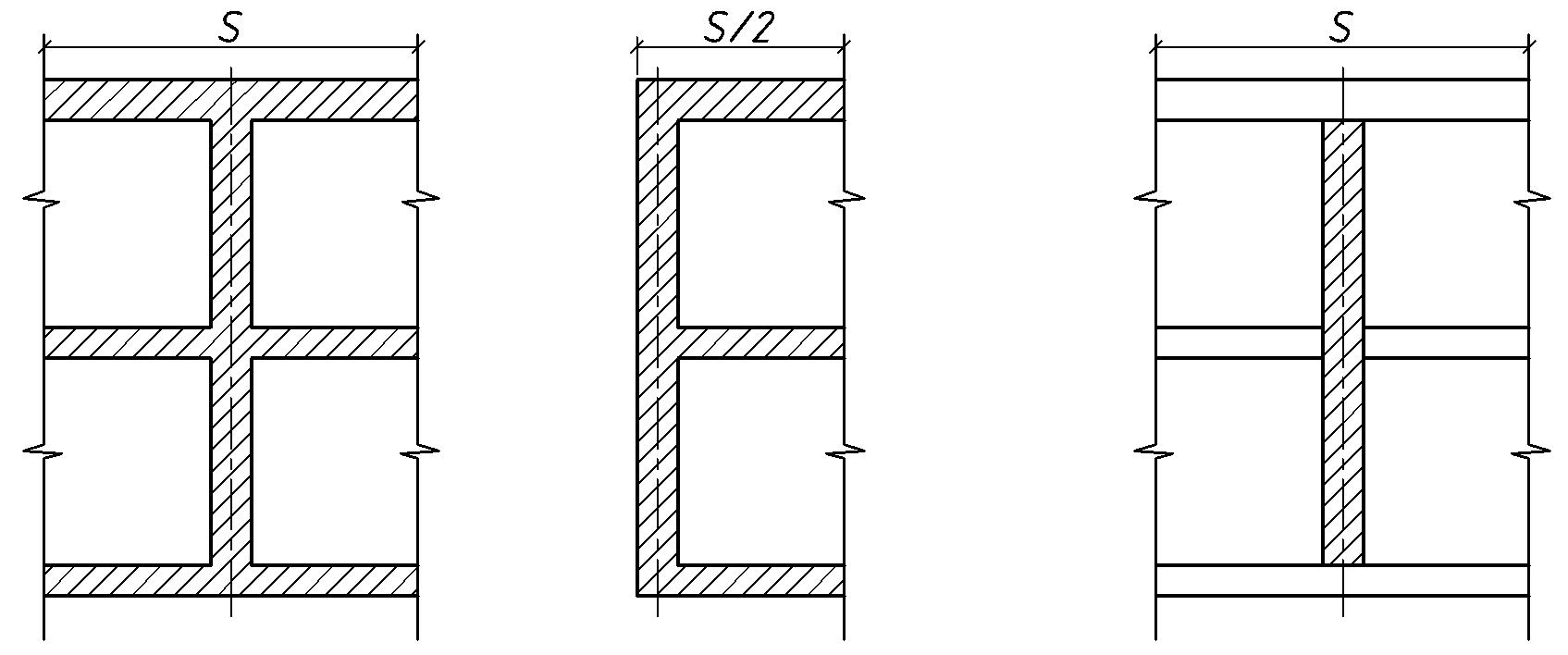
а б в

Рис.8.5. Розрахункові перерізи поперечних стін: а, б – при спільній роботі з поздовжніми стінами; в – за відсутності спільної роботи

Ширина цих ділянок, яку вводять у розрахунок, становить 1/3H₁ у кожен бік від краю поперечної стіни, але не більше 6h і не більше відстані від краю стіни до краю прилеглого простінка (H₁ - висота стіни, h - товщина прилеглої поздовжньої стіни).

При недостатній жорсткості вузла спряження поздовжні стіни до уваги не беруть і переріз консолей вважають прямокутним (рис. 8.5).

При симетричному та рівномірному розташуванні поперечних стін і при однаковій їх жорсткості вітрове розподілене навантаження w_k на 1 м висоти певної k-тої стіни на певному рівні i висоти будівлі дорівнює

w_k = w_i l, (8.6)

де l - відстань між поперечними стінами;

w_i - інтенсивність вітрового навантаження на рівні і, яка

складається з активної w_ai і пасивної w_рi складових.

У загальному випадку, коли поперечні стіни розташовані на різній відстані одна від одної, які мають різну жорсткість, вітрове розподілене навантаження на k-ту стіну будівлі визначають за формулою:

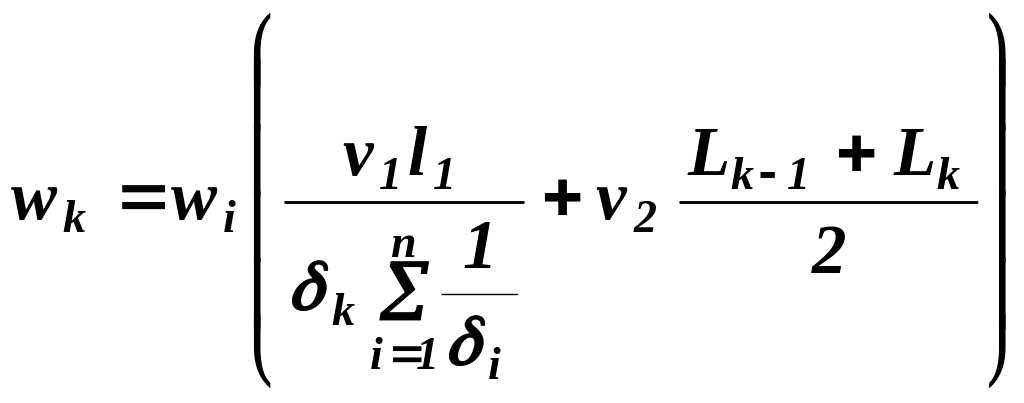, (8.7)

де v₁ i v₂ - коефіцієнти, що залежать від виду перекриття (при

монолітному залізобетонному v₁ = 0,9 ; v₂ = 0,1;

при збірних замонолічених перекриттях v₁ = 0,65 i

v₂ = 0,35 при дерев’яних перекриттях v₁ = 0,1 i

v₂ = 0,9);

L _k-1 , L_k - відстані між певною k -тою стіною і сусідніми

праворуч і ліворуч стінами;

_i , _k - горизонтальні переміщення стін на рівні 2/3

висоти стіни відносно планувальної відмітки землі,

викликані рівномірно розподіленим по висоті стін

навантаженням w = 1;

l₁ - довжина будівлі у напрямку, перпендикулярному до

тиску вітру;

n - число стін, паралельних до напрямку вітру.

Горизонтальні переміщення стін  складаються із двох складових:

_M - переміщення від згинального моменту

(деформація згину);

_Q - переміщення від поперечної сили (деформація

зсуву).

Другу складову враховують тільки при відношенні висоти стіни до висоти перерізу H / h  10.

Переміщення перерізу консолі на рівні 2/3Н при рівномірно розподіленому навантаженні можна отримати за формулами:

• від згину

; (8.8)

• від поперечної сили

, (8.9)

де A - площа перерізу консолі;

I - момент інерції перерізу відносно осі, що проходить

через центр його ваги;

E - модуль деформації кладки;

G - модуль зсуву, що становить 0,04 Е;

w - одиничне навантаження (w =1);

k – коефіцієнт, для прямокутного перерізу k =1,2;

для складного перерізу k визначають із формули:

, (8.10)

тут D_t ,D_b - геометричні величини, що характеризують

прямокутники, прилеглі безпосередньо до

нейтральної осі зверху та знизу (рис. 8.6), їх

визначають за формулою:

, (8.11)

де S - статичний момент відносно нейтральної осі усіх

прямокутників, які знаходяться вище над певним

прямокутником i, якщо він розташований вище

нейтральної осі (тобто при обчисленні D_t) або всіх

прямокутників нижче прямокутника і, якщо він

розташований нижче цієї осі ( тобто при обчисленні D_b).

Якщо поперечна стіна має розташовані один над одним прорізи, то її розглядають як систему вертикальних консолей (смужок між прорізами), пов’язаних між собою перемичками. При розрахунку перемичок їх розглядають як абсолютно жорсткі ригелі (розпорки), шарнірно зв’язані зі стінами.

У цьому випадку навантаження, яке сприймає кожна і-та ділянка (вертикальна смуга) стіни, визначають за формулою

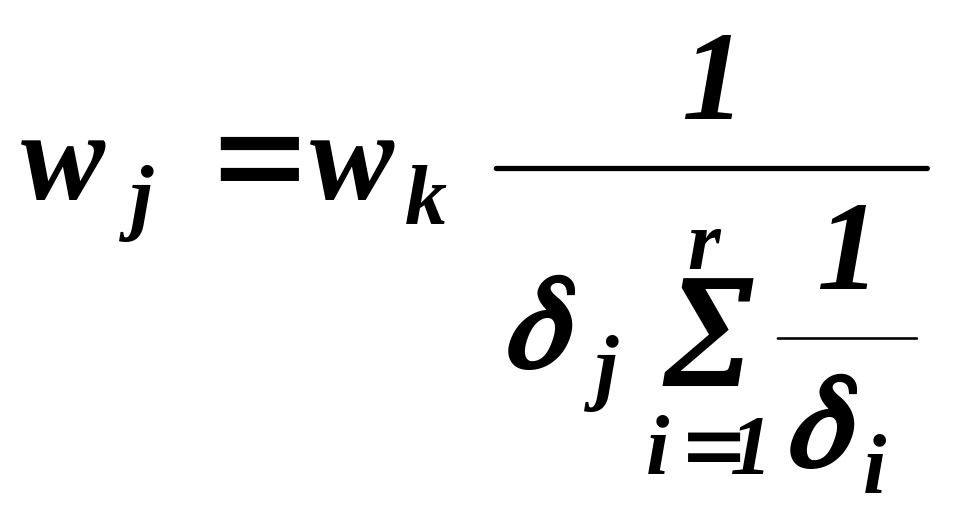, (8.12)

де _j - прогин розрахункової j-тої ділянки стіни при

одиничному розподіленому навантаженні на рівні 2/3Н₁;

_i - те ж , для i -тої ділянки стіни;

r - кількість вертикальних ділянок, на які стіна поділена

прорізами.

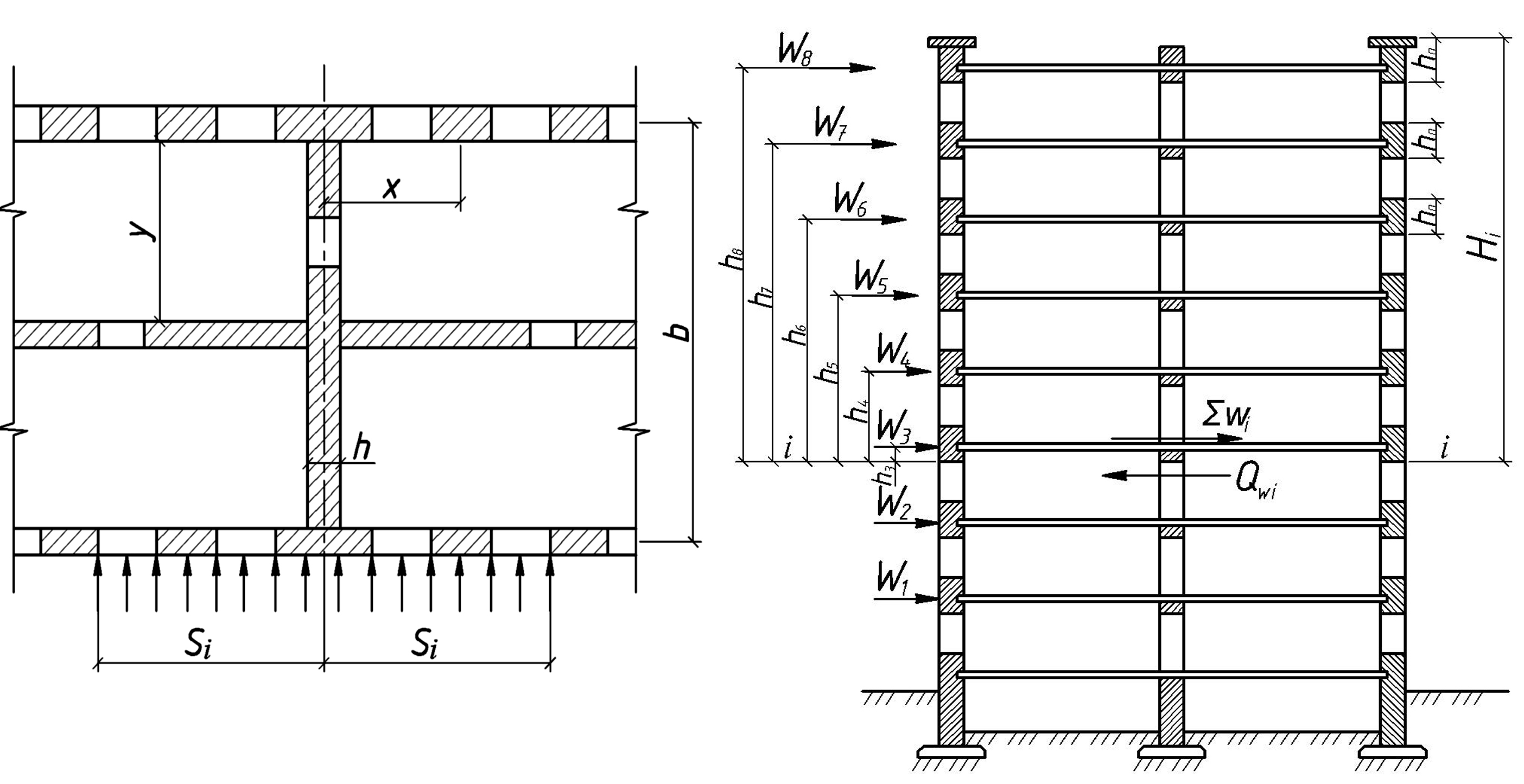
а) б)

Рис. 8.6. Схема будівлі при розрахунку на вітрове

навантаження: а – план; б - розріз

Розрахунковий тиск вітру на поперечну стіну, що передається одним перекриттям на висоті H_i, визначають із формули:

W_i = w_k H, (8.13)

де Н - висота поверху.

Повний розрахунковий тиск вітру W_i , що діє на консоль на рівні горизонтального перерізу i - i, дорівнює сумі розрахункових вітрових тисків W_i , які діють вище над певним перерізом. Наприклад, на рівні третього поверху (рис. 8.6)

W_i = Q_wi = W₃+ W₄+ W₅+ W₆+ W₇+ W₈ . (8.14)

В елементах консолі тиск вітру викликатиме такі зусилля і напруження:

1. Згинальний момент у перерізі i - i

M_wi = W_i h_i . (8.15)

Цей момент розвантажує поздовжню стіну з навітреного боку і довантажує поздовжню стіну з підвітреного боку, викликаючи у ній:

• додаткові вертикальні зусилля

; (8.16)

• напруження

_wi = N_wi / A , (8.17)

де h_i - відстань від точки прикладання сили W_i до певного

перерізу;

I - момент інерції перерізу консолі на рівні і - і;

y - відстань від осі поздовжньої стіни (простінка) до

нейтральної осі перерізу консолі;

x - відстань від осі простінка до осі поперечної стіни (при

глухих поздовжніх стінах х = 0);

S_i - розрахункова довжина ділянок поздовжніх стін з

кожного боку від осі поперечної стіни, що працюють

разом з нею;

A - площа поперечного перерізу цих ділянок стін; при

поздовжніх стінах із прорізами - площа поперечного

перерізу одного простінка.

Значення S_i приймають:

• для глухої стіни

S_i = 0,8 h_i ; (8.18)

• для стіни з прорізaми

, (8.19)

де h_i - відстань від верху поперечної стіни до рівня перерізу;

 h_n - сумарна висота горизонтальних поясів кладки між

віконними прорізами від верху стіни до певного

перерізу, тобто на ділянці h_i ;

A_b - площа перерізу поздовжньої стіни на ділянці S_i ;

A_n - загальна площа перерізу всіх простінків на цій ділянці.

Максимальне значення M_w і N_w знаходиться у горизонтальному перерізі І - І на рівні першого поверху (рис. 8.2). Нормальні напруження у поздовжніх стінах (простінках) _wi при згині приймають спадаючими за лінійною залежністю (рис. 8.2): від максимуму на осі поперечної стіни до нуля на відстані S_i від цієї осі.

Отримані зусилля N_wi або напруження _wi додають до зусиль від вертикальних навантажень.

Якщо розрахункове зусилля N_wi у простінку від вітрового навантаження менше 10% розрахункового зусилля від вертикальних навантажень або якщо нормативні напруження, викликані нормативним вітровим навантаженням, не перевищують 0,1 МПа, вплив вітрового навантаження на кам’яні стіни можна не враховувати.

2. Поперечна сила Q_wi = W_i викликає у стіні головні розтягувальні напруження, які визначають за формулою

_mt = Q_wi  / (hl), (8.20)

де h - найменша товщина ділянки поперечної стіни за умови,

що довжина цієї ділянки більша за 1/4 висоти поверху або

1/4 довжини стіни (за наявності у стіні каналів їх

ширина з товщини стіни виключається);

l - довжина поперечної стіни в плані;

 - коефіцієнт нерівномірності дотичних напружень у

перерізі; для двотаврових перерізів  =1,15, для

таврових  =1,35, а для прямокутних  =1,5.

Розрахунок поперечних стін на головні розтягувальні напруження зводиться до перевірки умови:

, (8.21)

де R_sh - розрахунковий опір сколюванню кладки, обтисненої

поздовжньою розрахунковою силою N, визначеною із

коефіцієнтом n = 0,9;

R_tw - розрахунковий опір кладки головним розтягувальним

напруженням;

_o - напруження обтиску кладки поздовжньою силою

_o = N/A , (8.22)

тут А - площа поперечного перерізу стіни.

Внаслідок жорсткого з’єднання поперечних і поздовжніх стін, у розрахунковий переріз вводять ділянки поздовжніх стін, прилеглих до поперечних стін. Достатня жорсткість цих вузлів має забезпечуватися умовою

, (8.23)

де Q - розрахункова поперечна сила від вітрового навантаження

поceредині висоти поверху;

y - відстань від осі поздовжньої стіни до осі, що проходить

через центр ваги перерізу стін у плані;

A - площа перерізу полиці (ділянки поздовжньої стіни);

I - момент інерції нетто перерізу стін відносно осі, що

проходить через центр ваги перерізу стін у плані;

h - товщина поперечної стіни;

H - висота поверху;

R_sq - розрахунковий опір кладки зрізу за перев’язаним

перерізом.

Якщо умова (8.23) не забезпечена, то поздовжні стіни в роботі не враховують і переріз поперечної стіни вважається прямокутним.