2.2 Определение скоростей точек и угловых скоростей звеньев

Наиболее просто и наглядно поставленная задача может быть решена методом плана скоростей.

План скоростей строим последовательно для отдельных структурных составляющих механизма в порядке, соответствующем синтезу механизма.

Последовательность построения плана скоростей для одного положения механизма:

• Определяем скорость точки кривошипа, к которой присоединена первая группа Ассура, и строим вектор скорости этой точки в масштабе μ_V из точки Р, называемой полюсом плана скоростей. Конец вектора обозначаем той же буквой (только строчной), что и соответствующая точка на плане положений.

• Составляем векторные уравнения абсолютных скоростей точек в виде суммы переносной и относительной скоростей. В качестве переносного принимаем движение точки, скорость которой известна, а относительное движение определяем в связи с этой точкой. Полученные уравнения решаем графически с использованием уже построенного вектора и известных направлений относительных скоростей.

• Определяем истинные значения абсолютной и относительной скоростей рассматриваемой точки с помощью масштабного коэффициента.

• Определяем величины и направления угловых скоростей звеньев, совершающих вращательное или плоскопараллельное движение, с помощью найденных относительных скоростей.

• С помощью принципа подобия в плане скоростей, определяем скорость той точки данной группы Ассура, к которой свободным элементом кинематической пары присоединена следующая структурная группа, и строим вектор скорости этой точки на плане.

В таком же порядке строим план скоростей и определяем все кинематические параметры для последующих групп Ассура.

Построенный таким образом план скоростей механизма обладает следующими свойствами:

• абсолютные скорости точек изображаем векторами, начинающимися в полюсе и заканчивающимися в точке с соответствующим обозначением (т.е. на плане – это лучи, выходящие из полюса. Скорости точек, совпадающих с полюсом, равны нулю.);

• относительные скорости точек изображаем векторами, соединяющими соответствующие точки на плане, причем вектор направлен в сторону той точки, относительное движение которой рассматриваем (к первой букве индекса относительной скорости);

• относительные скорости точек жесткого звена на плане скоростей образуют фигуру, подобную самому звену на плане положений, что позволяет определить скорость любой точки звена, если скорости каких-либо двух точек этого звена уже известны;

• план скоростей позволяет определить величины и направления угловых скоростей звеньев механизма путем переноса векторов в соответствующую точку плана положений.

При построении плана скоростей следует помнить, что не только точность определения скоростей, но и наглядность полученного плана зависит от длин векторов (следовательно, от масштабного коэффициента). Вектор скорости, с которого начинается построение плана, изображаем отрезком не менее 100 мм.

По заданию кривошип вращается по часовой стрелке с угловой скоростью

₁ = 1. Скорость точки А, принадлежащей оси шарнира, т.е. одновременно концу кривошипа и камню кулисы, равна

υ_А = ₁ L_ОА, (2.1)

υ_А = 1 · 35 = 35 = 0,35 м/с.

и направлена перпендикулярно положению звена ОА в сторону, соответствующую угловой скорости. Выбрав полюс Р и величину отрезка Ра, изображающего скорости точки А (Ра = 100 мм), построим этот вектор и определим масштабный коэффициент

(2.2)

Рассмотрим группу Ассура, присоединенную к кривошипу и состоящую из звеньев 2 и 3 (см. рис. 1.1), т.е. из кулисы 3 и камня 2. Скорости точек А и В известны: скорость точки А только что найдена, а скорость точки В равна нулю (υ_В = 0), т.к. она одновременно принадлежит и стойке. Следовательно, мы можем определить скорость точки, принадлежащей средней кинематической паре этой группы. Обозначим эту точку буквой А`, поскольку на плане положений она совпадает с точкой А, но принадлежит другому звену – кулисе 3. Составим два векторных уравнения, связывающих скорость точки А`, с известными скоростями точек А и В:

(2.3)

 О₁А₁, υ_О1 = 0). (2.4)

где 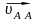– вектор скорости в относительном поступательном движении точки А` кулисы относительно точки А камня (направление ее известно – вдоль кулисы, т.к. поступательная пара между звеньями 2 и 3 никакого другого относительного движения не допускает);

– вектор скорости в относительном вращательном движении точки А` относительно точки О₁ (направление ее также известно – перпендикулярно кулисе, т.к. скорость во вращательном движении всегда перпендикулярна радиус-вектору точки).

Решить систему векторных уравнений можно, если число неизвестных составляющих (величин и направлений) векторов, входящих в систему, не превышает удвоенного количества уравнений. В данном случае система содержит четыре неизвестные составляющие: величину и направление вектора 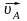, величину вектора и величину вектора . Следовательно, система решается.

Для решения системы необходимо в масштабе, используя правило сложения векторов, построить эти уравнения из одной точки Р. Вектор Ра, изображающий скорость υ_А, на плане уже есть; вектор скорости необходимо с ним сложить, поэтому через конец вектора 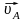(через точку а на плане скоростей) проводим известное направление (линию, параллельную О₁А₁). Это все, что пока можно получить из первого уравнения системы.

Из второго уравнения: скорость υ_В = 0, следовательно, этот вектор представляет из себя точку, совпадающую с полюсом Р. Вектор , направление которого известно, необходимо сложить с вектором 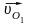, для чего через конец вектора (т.е. полюс) проводим нужное направление (линию, перпендикулярную О₁А₁) до пересечения с уже проведенной через точку а линией. Точка их пересечения и дает искомое решение системы уравнений, т.е. определяет конец вектора скорости υ<sub>А`</sub>, поэтому на плане скоростей эта точка получает обозначение а`.

Действительное значение скорости точки А` равно

υ<sub>А`</sub> = Ра` μ_υ, (2.5)

υ_А`1 = 80 · 0,0035 = 0,28 м · с^-1,

υ_А`2 = 98 · 0,0035 = 0,343 м · с^-1,

υ_А`3 = 48 · 0,0035 = 0,168 м · с^-1,

υ_А`4 = 57 · 0,0035 = 0,199 м · с^-1,

υ_А`5 = 94 · 0,0035 = 0,329 м · с^-1,

Отрезок аа` на плане изображает скорость υ<sub>А`А</sub>, ее действительное значение также может быть определено произведением длины отрезка аа` на масштабный коэффициент μ_υ

υ<sub>А`А</sub> = аа` μ_υ, (2.6)

υ_А`А1 = 61 · 0,0035 = 0,22 м/с^-1,

υ_А`А2 = 18 · 0,0035 = 0,063 м/с^-1,

υ_А`А3 = 88 · 0,0035 = 0,31 м/с^-1,

υ_А`А4 = 82 · 0,0035 = 0,29 м/с^-1,

υ_А`А5 = 33 · 0,0035 = 0,115 м/с^-1,

Скорость υ<sub>А`А</sub> направлена от точки а к точке а` на плане скоростей.

Далее определим угловую скорость звеньев 2 и 3 (₂ = ₃), т.к. вращательное движение для них общее (относительное движение - поступательное)

₂ = ₃ 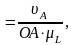(2.7)

₂₁ =

₂₂ =

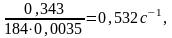
₂₃ =

₂₄ =

₂₅ =

Вектор скорости точки А` относительно точки В равен вектору абсолютной скорости точки А`, т.е. υ_{А`В</sub> = υ<sub>А`}. Расстояние от точки А` до точки В (L<sub>А`В</sub>) может быть определено с помощью плана положений. Направление угловой скорости ₃ определяется следующим образом: мысленно перенесем вектор скорости υ<sub>А`В</sub> в соответствующую точку плана положений (точку А`) и рассмотрим ее движение относительно точки В; ясно, что вращение звена 3 осуществляется по часовой стрелке, что и показано круговой стрелкой на плане положений механизма в положении 1. Затем в соответствии с предложенной выше последовательностью следует определить скорость точки В, к которой присоединена следующая группа Ассура. Воспользуемся принципом подобия: т.к. точки В, А`, С, принадлежащие одному жесткому звену, расположены на плане положений на одной прямой, то и точки b, (она же – полюс Р) а`, с тоже должны располагаться на одной прямой на плане скоростей. Из подобия фигур имеем

(2.8)

следовательно

Рв = (2.9)

_Рв1 =

Рв₂ =

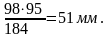
Рв₃ =

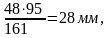
_Рв4 =

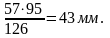
_Рв5 =

_{Найдём Рв` , О1В1 принимаем по чертежу.}

_Рв1^/ = _’

_Рв1^/ = _’

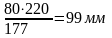_Рв2^/ = _’

_Рв3^/ = _’

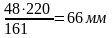_Рв4^/ = _’

Рв₅^/ =

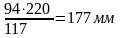
Построим этот вектор на плане скоростей и определим

υ_с = Рс μ_v=вс_υμ_v , (2.10)

υ_с1 = 4 · 0,0035 = 0,014 м/с,

υ_с2 = 5 · 0,0035 = 0,018 м/с,

υ_с3 = 7 · 0,0035 = 0,025 м/с,

υ_с4 = 9 · 0,0035 = 0,032 м/с,

υ_с5 = 6 · 0,0035 = 0,021 м/с,

Теперь можно переходить к рассмотрению второй и последней в данном механизме группы Ассура, состоящей из звеньев 4 и 5 (см. рис. 1.1), т.е. из шатуна СВ и ползуна. Необходимо определить скорость точки В, принадлежащей вращательной кинематической паре, т.е. одновременно звену CВ и звену В. Т.к. звено 5 совершает поступательное движение, а значит скорости всех точек этого звена равны и направлены в одну сторону – вдоль направляющей, то известно направление скорости точки В. Скорость точки С определена выше по правилу подобия. Составим векторное уравнение, связывающее скорости точек С и В:

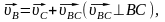
направляющей,

где - вектор скорости в относительном вращательном движении точки В относительно точки С, следовательно, направление этого вектора перпендикулярно положению звена СВ на плане положений.

Т.к. полученное уравнение содержит всего две неизвестные составляющие – величины векторов и , то оно может быть решено. Для этого через точку С₁ на плане скоростей проведем линию, перпендикулярную положению звена СВ на плане положений, а через полюс – линию, параллельную направляющей (вертикальную линию). Точка их пересечения есть точка В₁ – конец вектора Рв, изображающего на плане скорость точки В. Тогда

υ_В = Рв μ_υ , (2.11)

υ_В1 = 43 · 0,0035 = 0,15 м/с,

υ_В2 = 51 · 0,0035 = 0,178 м/с,

υ_В3 = 28 · 0,0035 = 0,098 м/с,

υ_В4 = 43 · 0,0035 = 0,15 м/с,

υ_В5 = 76 · 0,0035 = 0,266 м/с,

Отрезок В₁С₁ на плане скоростей изображает скорость υ_ВС, которая направлена на плане в сторону точки В₁. Угловая скорость звена CВ (₄) может быть определена

(2.12)

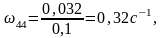
Для определения направления угловой скорости звена CВ следует мысленно поместить вектор относительной скорости υ_ВC в соответствующую точку плана положений, т.е. в точку В. Очевидно, что под действием этого вектора звено вращается по часовой стрелке (см. план положений). Т.о. строим планы скоростей для всех положений механизма, приведенных на плане положений. Все планы строим из одного полюса. Результаты расчетов сводим в таблицу 1.2, а также для выполнения раздела курсового проекта «Динамика механизмов» необходимо знать скорости центров масс звеньев (υ_S3 и υ_S4), поэтому их значения определяем по правилу подобия для всех положений и также вписываем в таблицу 1.2.

υ_S3 = PS₃ μ_υ, (2.13)

υ_S31 = 10 · 0,0082 = 0,08 м · с^-1,

υ_S4 = S₄ μ_υ, (2.14)

υ_S41 = 80 · 0,0082 = 0,66 м · с^-1.

Таблица 2.1

Значения скоростей точек и угловых скоростей звеньев механизма

Положение механизма Кинематич. параметры	0(6)	1	2	3	k	4	5
υА	0,35	0,35	0,35	0,35	0,35	0,35	0,35
υА`	0	0,28	0,343	0,168	0	0,2	0,329
υВ	0	0,15	0,178	0,098	0	0,15	0,266
υС	0	0,14	0,018	0,025	0	0,32	0,021
3	0	0,45	0,532	0,29	0	0,45	0,8
4	0	0,14	0,18	0,25	0	0,32	21
υS3	0	21,5	25,5	14	0	21,5	38
υS4	0	2	2,5	3,5	0	4,5	3