8.1. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (выборки незпвисимы).

Рассмотрим случай, когда генеральные дисперсии и известны. Поскольку, значения E[x] и E[y] неизвестны, то для проверки Н_о используем их наилучшие оценки и .

Параметры и подчинены нормальному закону распределения с числовыми характеристиками E[x], /n, E[y], /n. Выборки независимы поэтому параметры и также независимы, а случайная величина [  ] имеет нормальное распределение, причем D[  ]= .

Если гипотеза Н_о справедлива, то E[  ]= Е[ ]  Е[ ] = 0, следовательно нормированная разность

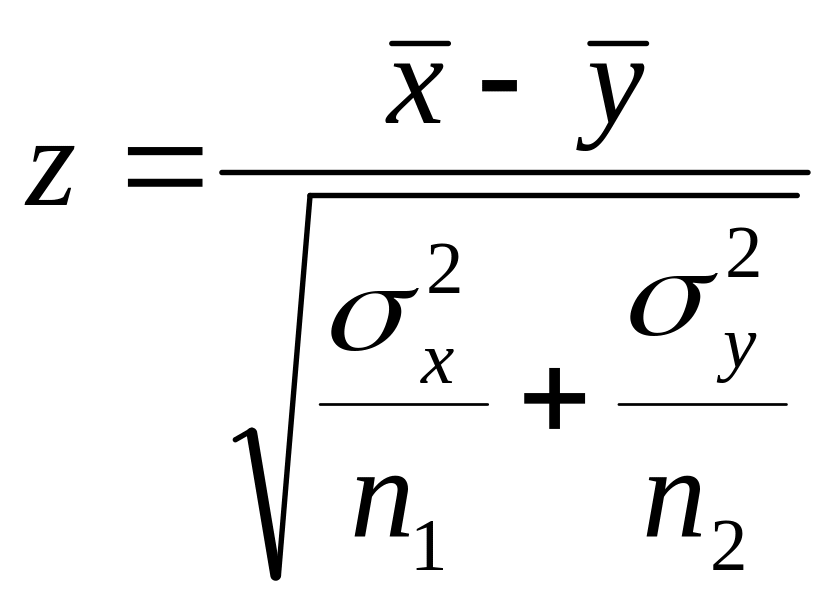
подчиняется нормальному закону распределения с параметрами E[z]=0, D[z]=1. В силу конкурирующей гипотезы Н₁:Е[х]E[y] необходимо формировать двухстороннюю область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы Н_о была равна принятому уровню значимости . Наибольшая мощность критерия (вероятность попадания значения критерия в критическую область при справедливости H₁) достигается тогда, когда левая и правая критические точки выбраны так, что вероятность попадания значения критерия в каждый из двух интервалов критической области равна /2.

P{z < } = /2; P{z > } = /2.

Поскольку распределение z симметрично относительно нуля, критические точки симметричны относительно нуля. Таким образом, область принятия нуле­вой гипотезы Н_о есть ( , )

Используя функцию Лапласа определим , — правую границу двухсто­ронней критической области.

Функция Лапласа определяет вероятность попадания нормированной нормальной случайной величины Z в интервале (0,z) P(0<Z<z)Ф(z). Так как распределение Z симметрично относительно нуля, то вероятность попадания Z в интервал (0,) равна 1/2. Разобьем этот интервал точкой , на

подинтервалы (0, ) и ( ,). По теореме сложения вероятностей имеем:

P(0<Z< )+P(Z< )=1/2 или Ф( )+/2=1/2

Следовательно, Ф( ) =(1)/2 Откуда при заданном  определяем ,. Итак, для проверки Н_о необходимо вычислить эмпирическое значение критерия

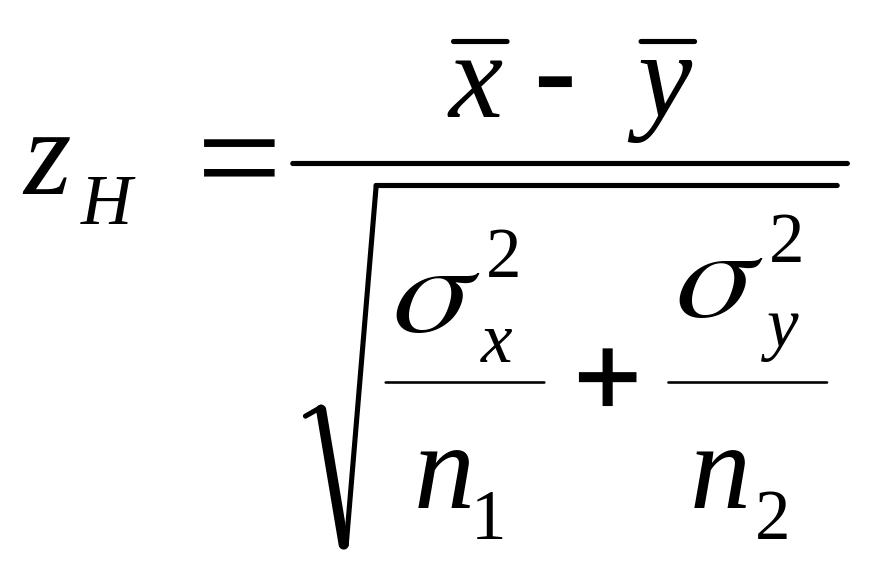
и по таблице функции Лапласа найти критическую точку по равенству Ф( ) =(1)/2

Если |z_H|< ,  нет оснований отвергнуть нулевую гипотезу H_o.Если |z_H|<  Н_o — отвергают.

Пример. По двум извлеченным выборкам, извлеченным из двух нормаль­ных генеральных совокупностей, объемы которых соответственно равны n₁ = 60 и n₂ ⁼ 50 определены выборочные средние =1250 и =1275. Генеральные дисперсии известны: D_x = 120, D_y = 100.

При уровне значимости  = 0.01 проверить Н_о: E[x]=E[y] при конкурирующей гипотезе Н₁ :E[x] E[y].

Решение. Найдем эмпирическое значение критерия z_H= 12.5. По условию, конкурирующая гипотеза имеет вид E[x] E[y], поэтому критическая область - двухсторонняя. Найдем правую критическую область

Ф( ) =(1)/2= 0.495.

По таблице функции Лапласа находим =2.58. Так как |z_H|> то нулевую гипотезу Н_о отвергаем.

Рассмотрим случай, когда конкурирующая гипотеза имеет вид H₁:E[x]>E[y]. Так например, введено усовершенствование технологического процесса, то естественно предположить, что оно приведет к увеличению вы­пуска продукции. В этом случае строят правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости Н_о была равна принятому уровню значимости

 P(z>z_kp)=.

Найдем критическую точку с помощью функции Лапласа и соотношения

P(0<z< )+P(z< )=1/2

Откуда имеем Ф( )+ /2=1/2. Следовательно Ф( ) = (1)/2, что позволяет найти .

Если z_H < , то нет оснований отвергнуть нулевую гипотезу Н_о, в противном случае Н_о отвергаем.

Пример. По двум независимым выборкам, извлеченным из нормальных генеральных совокупностей, объемы которых равны n₁ = 10,n₂ =10, найдены выборочные средние =14.3 и =12.2. Генеральные дисперсии известны D_x = 22, D_y = 18. При уровне значимости  проверить нулевую гипотезу

Н_о: E[x]=E[y], при конкурирующей гипотезе Н₁:E[x]>E[y].

Решение. Найдем эмпирическое значение критерия

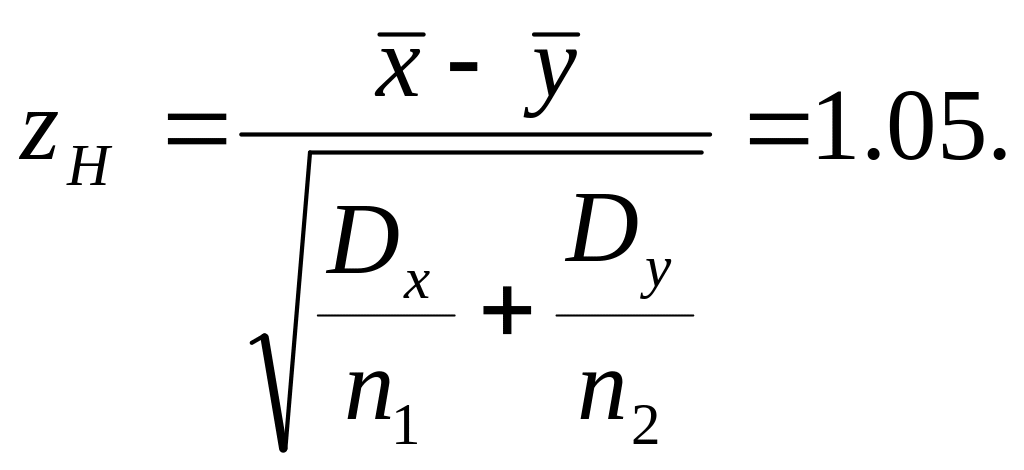
Конкурирующая гипотеза имеет вид Е[х] > E[y], поэтому критическая область - правосторонняя. По таблице функции Лапласа находим = 1.64. Так как z_H < , то нет оснований отвергнуть Н_о.

Рассмотрим случай, когда конкурирующая гипотеза имеет вид Н₁:Е[x]<Е[у]. В этой ситуации формируют левостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы Н_о, но была равна принятому уровню значимости P(z< )=.

Критерий z распределен симметрично относительно нуля, следовательно критическая точка симметрична такой точке > 0, для которой P(z> )=., т. е. =  . Таким образом, для того, чтобы найти , достаточно найти так, как описано во втором случае, а затем взять найденное значение со знаком минус.

Решающее правило проверки Н_о: если z_H > ,то нет оснований от­вергнуть нулевую гипотезу Н_о, в противном случае Н_о отвергают.

Пример. По двум независимым выборкам, извлеченным из нормальных генеральных совокупностей, объемами n₁=50,n₂ =50 найдены выборочные средние =142 и =150. Генеральные дисперсии известны D_x = 28.2 и D=22.8. При уровне значимости  = 0.01 проверить Н_о:E[x]<Е[у] при конкурирующей гипотезе Н₁: Е[x] < E[ у].

Решение. Найдем эмпирическое значение критерия z_H = 8. Конкури­ующая гипотеза имеет вид E[x]<E[y] поэтому критическая область  левосторонняя. Найдем вспомогательную точку с помощью уравнения

Ф( ) = (1 — )/2 = 0.49 и таблицы функции Лапласа (см. прил. 7) = 2.33. Так как z_H < - , то нулевую гипотезу отвергаем.