
- •Краткая теория по математике. Формулы сокращенного умножения.
- •Функции. Основные понятия и определения.
- •Графики элементарных функций.
- •Пределы.
- •Замечательные пределы
- •1. Первый:
- •2. Второй:
- •Производная
- •Геометрический смысл производной.
- •Физический смысл производной.
- •Степени и арифметические корни
- •Квадратные уравнения
- •Тригонометрические преобразования и вычисления
- •Экстремум функции
- •Соотношения между сторонами и углами в треугольнике
- •Признаки равенства и подобия треугольников.
Краткая теория по математике. Формулы сокращенного умножения.
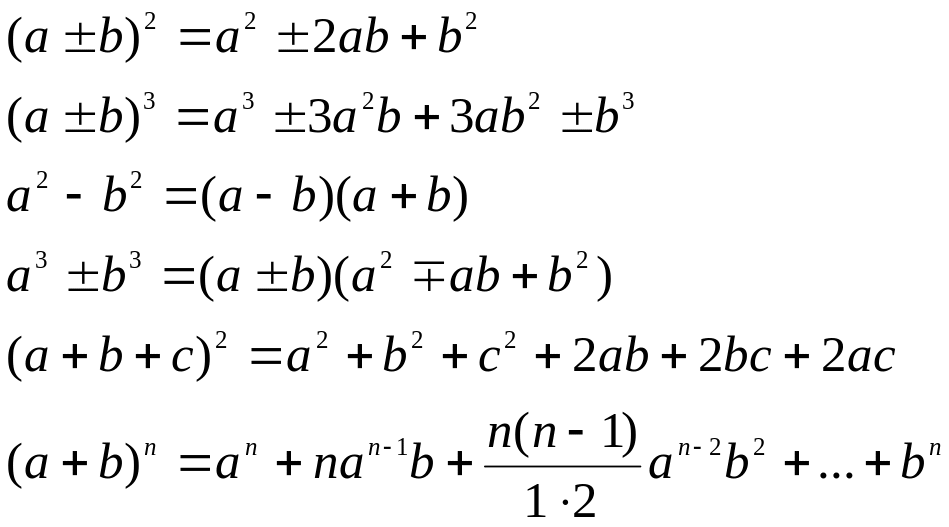
Пример.
Упростить
выражение![]()
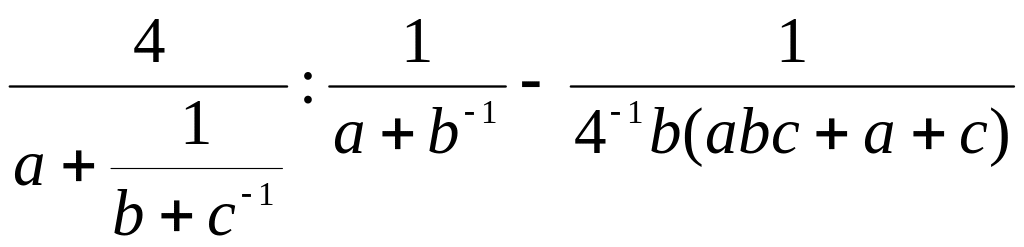
Функции. Основные понятия и определения.
Функцией у = f(x) называют зависимость переменной у от переменной х, при которой каждому допустимому значению х соответствует единственное значение у .
Область определения функции D(f) - множество всех допустимых значений переменной х.
Область значения функции E(f) - множество всех допустимых значений переменной у.
Функция монотонна, если она либо только возрастает, либо только убывает на D(f).
Функция четна, если:
f(x) = f(-x) .
График четной функции симметричен относительно оси Оу .
Функция нечетна, если: f(x) = -f(-x).
График нечетной функции симметричен относительно точки 0.
Функция
у
= f(x)
является периодической, если существует
такое число
![]() ,
,
при котором для всех х из области определения функции выполняется равенство
![]()
![]()
Графики элементарных функций.
Графиком
функции
![]() называют множество точек плоскости,
координаты которых удовлетворяют данной
функциональной зависимости и представляет
собой некоторую линию на плоскости.
называют множество точек плоскости,
координаты которых удовлетворяют данной
функциональной зависимости и представляет
собой некоторую линию на плоскости.
1. Линейной называют функцию вида у = kx+b, где k и b некоторые действительные числа. Если b=0, то функция принимает вид у= kx и называется прямой пропорциональностью. Графиком линейной функции является прямая.
2.
Обратной
пропорциональностью
называют
функцию вида![]() ,
где k
- отличное от нуля действительное число.
Графиком функции
,
где k
- отличное от нуля действительное число.
Графиком функции
![]() является гипербола.
является гипербола.
Если k > 0, то график функции расположен в первой и третьей четверти координатной плоскости.
Если k < 0, то график функции расположен во второй и четвертой четверти координатной плоскости.
Например,
![]()
![]() ,
,
![]()
3. Степенной называют функцию вида у = хп, где п - действительное число, отличное от нуля.
Например:
a)
если n=2,
то y=x2
,б) если n=3,
то y=x3,
в)
если
![]() ,
то
,
то
![]() или
или
![]()
в)
если
![]() ,
то
,
то
![]() или
или
![]()
4. Показательной называют функцию вида у = ах, где а - const, а> 0 и a≠1
Графиком показательной функции является экспонента. Если, а > 1, то функция монотонно возрастает.
Например, у = 2х
5. К тригонометрическим относят функции:
1)![]() ;
основной период функции
;
основной период функции
![]()
2)![]() ;
основной период функции
;
основной период функции
3)![]() ;
основной период функции
;
основной период функции
![]()
4)![]() ;
основной период функции
;
основной период функции
Векторы. Действия над векторами.
Пределы.
Функция f(x) имеет предел a в точке x0, если для всех значений x близких к x0 значение f(x) близко к a.
![]() ;
; ![]()
Свойства пределов числовых функций:
1. Одна и та же функция в одной и той же точке может иметь только один предел.
2. Предел суммы (разности) двух функций равен сумме (разности) пределов этих функций:
Если
и
![]() ,
то
,
то
![]()
3. Предел произведения функций равен произведению пределов:
Если
и
,
то
![]()
4. Предел частного равен частному пределов:
Если
и
,
то
![]()
Замечательные пределы
1. Первый:
![]()
Следствия
![]() ;
;
![]() ;
;
![]()
2. Второй:
![]() – число
Непера Следствия
– число
Непера Следствия
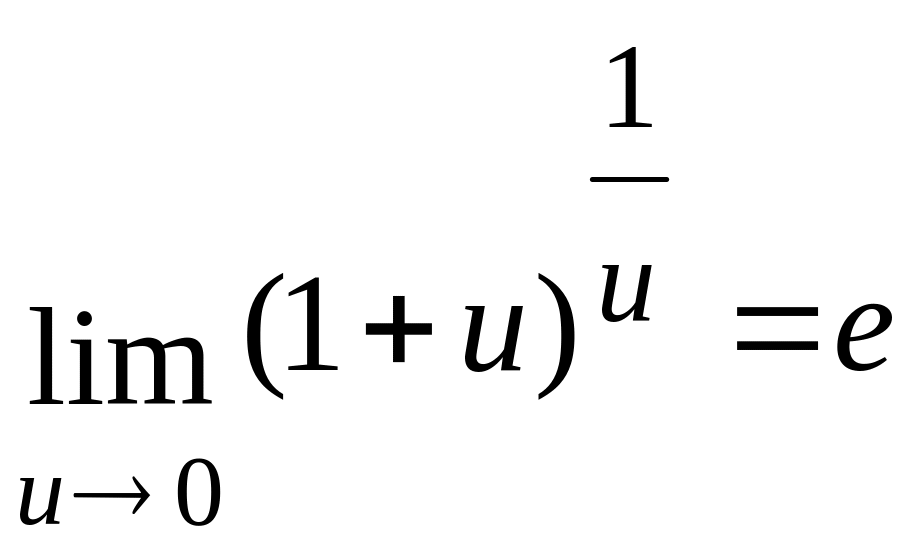 ;
;
![]() ;
;
![]() ;
;
![]() ;
; ![]() для а>0 и
а≠1
для а>0 и
а≠1
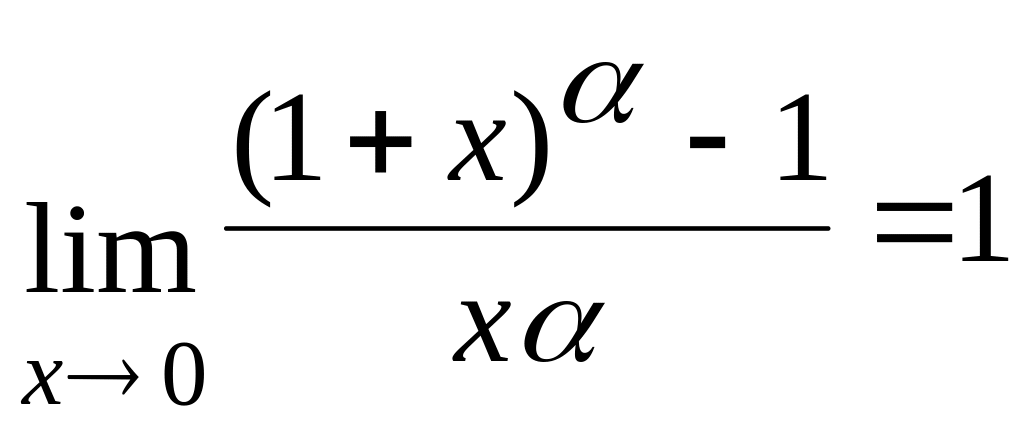 Примеры:
Примеры:
а)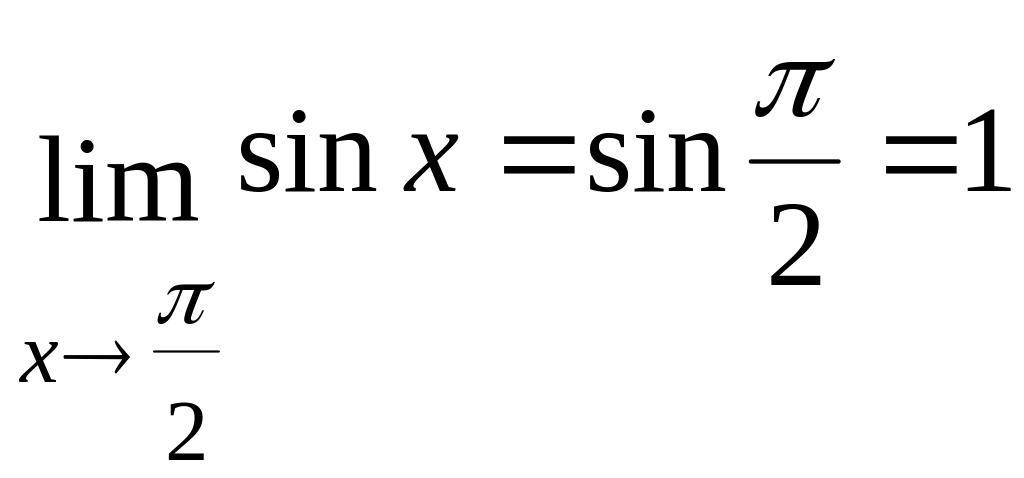 б)
б)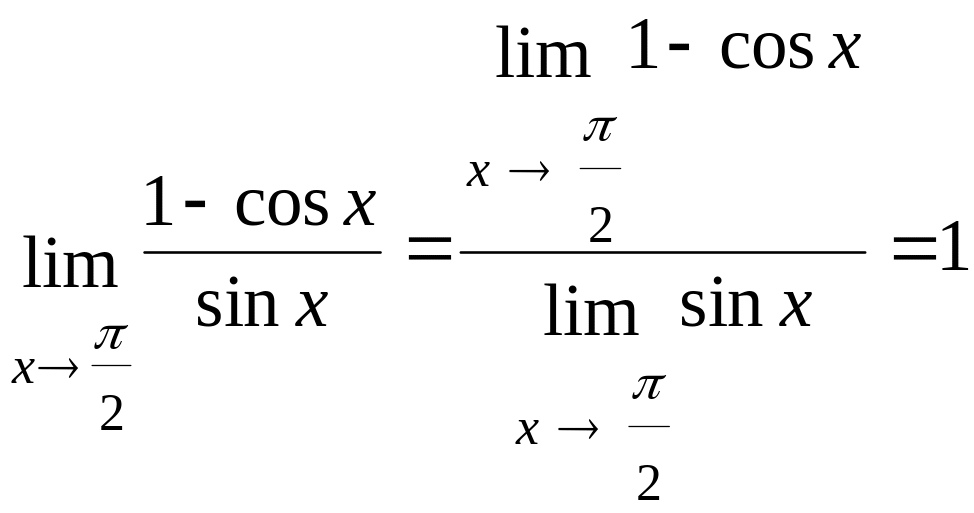
в) г)
г)
![]()
Производная
Пусть в некоторой окрестности точки x0 определена функция f(x).
Производной функции f(x)называется предел, если он существует:
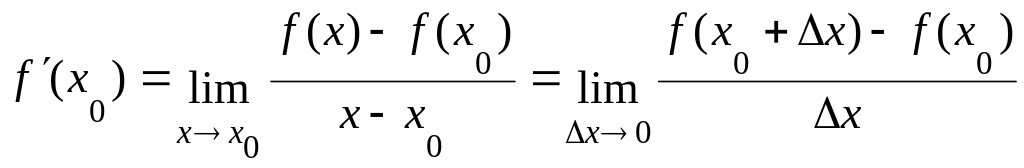
Общепринятые обозначения
![]()
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с суммами, произведениями, частными функций, а также сложными функциями (функциями от функций).
Правила дифференцирования.
Если С – постоянное число и f(x)=f, g(x)=g – некоторые дифференцируемые функции, то
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; 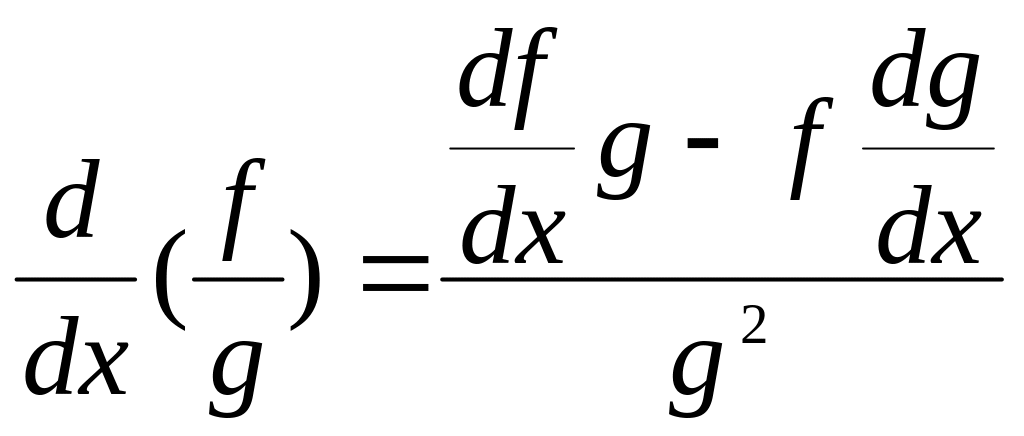 ;
;
![]() – правило
дифференцирования сложной функции
– правило
дифференцирования сложной функции
