Глава 10 защита от вибрации
Развитие механизации в строительстве и промышленности строительных материалов вызвало широкое использование вибрационной техники, мощных строительных машин и механизмов. В результате возрастает число людей, подвергающихся неблагоприятному воздействию высоких уровней вибрации.
Шум, как правило, является следствием вибрации и поэтому на практике часто рабочие испытывают совместное неблагоприятное действие шума и вибрации. Воздействие вибрации не только отрицательно сказывается на здоровье, ухудшает самочувствие, снижает производительность труда, но иногда приводит к профессиональному заболеванию — виброболезни. По данным Всемирной организации здравоохранения повышенные уровни вибрации и шума являются ведущими факторами в возникновении сердечнососудистых заболеваний.
Основными источниками вибрации и шума являются машины для приготовления, распределения и виброуплотнения бетонной смеси: бетоносмесители, дозаторные установки, виброплощадки, а также строительные машины, компрессоры, бульдозеры и др.
Ручной механизированный инструмент с электро- и пневмоприводом передает интенсивные вибрации на руки рабочего и характеризуется высоким уровнем шума.
При работе машин и механизмов низкочастотные вибрации вызываются инерционными силами, силами трения, периодическими рабочими нагрузками. Высокочастотные вибрации возникают в результате ударов из-за наличия зазоров в соединениях механизмов, ударов в зубчатых и цепных передачах, соударений в подшипниках качения.
10.1. Физические характеристики вибрации
Колебаниями в технике называют движения, обладающие определенной повторяемостью во времени. Простейшими колебаниями являются гармонические, при которых переменная величина изменяется по закону синуса или косинуса:
X = Xosinωt (10.1)
где X — амплитуда виброперемещения; ω— круговая частота колебаний.
По способу возбуждения колебания могут быть свободными или вынужденными. Свободные (или собственные) колебания — это такие колебания, которые совершает механическая система, обладающая упругостью и массой, после выведения из состояния равновесия. Характер свободных колебаний (частота, продолжительность) зависит только от свойств самой системы — массы, упругости, сил затухания.
Рассмотрим свободные незатухающие колебания механической системы, состоящей из массы М, подвешенной на безмассовой пружине, обладающей жесткостью K.
Жесткость — это величина, численно равная силе (Н), которую необходимо приложить к упругому элементу, чтобы получить единичную деформацию, например в 1 см.
Предлагаем,
что силы, вызывающие затухание
колебаний груза, отсутствуют;
колебания происходят только в вертикальной
плосккости; крутильными колебаниями
пренебрегаем. При колебаниях
действующие в системе внутренние
силы — упругая сила пружины КХ
и
инерционная сила
—
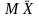должны динамически
быть уравновешены. Поэтому
уравнение сил, действующих внутри
системы
в каждый момент времени, можно представить
в виде
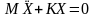(10.2)
Решением этого уравнения является синусоидальная функция.
Дифференцируя по времени уравнение (10.1), находим скорость X и ускорение X колебательного движения:
(10.3)
Поставив уравнения (10.1) и (10.3) в уравнение (10.2), находим значение находим значение круговой частоты собственных колебаний (с-1)
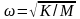. (10.4)
Круговая частота собственных колебаний механической системы зависит от массы груза и жесткости пружины.
Принимая во внимание, что период колебаний Г(с) (т. е. время одного полного колебания) связан с круговой частотой (с~!), отношение
,
(10.5)
частоту собственных колебаний (Гц) можно выразить в виде
(10,6)
По формуле (10.6) с достаточной точностью (без учета затухания) можно определить частоту собственных колебаний большинства встречающихся в инженерной практике колебательных систем.