7. Прийняття багатоступеневих рішень. Використання схеми “дерева” рішень для розрахунку та порівняння альтернатив при невизначеності наслідків. Вибір в умовах статистичних рішень.

Cхему “дерева” рішень використовують, коли необхідно прийняти декілька рішень в умовах невизначеності, коли кожне наступне рішення залежить від попереднього, або ж від результатів випробувань.

Дерево рішень відображає структуру проблеми. Зображають дерево зліва направо. Гілки означають можливі альтернативні рішення, що можуть бути прийняті і можливі наслідки, що виникнуть внаслідок цих рішень. Використовують два види гілок:

1. пунктирні лінії, що з’єднують квадрати можливих рішень;

2. суцільні лінії, що з’єднують, круги можливих результатів.

Квадратні вузли означають місця, де приймаються рішення, круглі вузли – появу результатів. Через те, що ОПР не може впливати на появу результатів, вона обмежується лише обчисленням ймовірностей їх виникнення.

Після того, як усі можливі рішення та їх наслідки вказані на дереві, розраховують кожен із варіантів і в кінці проставляють його вартісну оцінку. Усі витрати, пов’язані з рішенням, проставляються на відповідній гілці.

Приклад. Клієнт звернувся до банку за позикою, розміром 15 тис.у.о. для фінансування свого проекту. Банк може позичити йому гроші під 15% річних, або ж вкласти їх в інвестиційний проект під 9% річних із надійним 100% поверненням суми. Із попереднього досвіду відомо, що 4% клієнтів кредит не повертають. Задача перед банком – чи позичати клієнту гроші.

Перший варіант рішення: вирішуємо за схемою “матриці” рішень (табл.14).

Таблиця 14. Матриця рішень

Варіанти рішень	Можливі результати та їх ймовірності		BL	MM
	Клієнт кредит повертає(0,98)	Клієнт кредит не повертає (0,04)
Видавати кредит	15000 + 2250= 17250	0	1560	0
Вкласти гроші в інвестицію	15000 + 1350= 16350	16350	1350	1350

17250 · 0,96 + 0·0,04 = 16560

Очікуваний прибуток 16560 – 15000 = 1560

Другий варіант рішення: за схемою “дерева” рішень (рис.2).

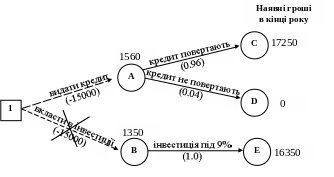
Рис.2 . Дерево рішень.

Прибуток в точки А = 17250*0,96 + 0*0,04 = 16560

Чистий прибуток в вузлі А = 16560 – 15000 = 1560

Прибуток в точки В = 16350*1

Чистий прибуток в вузлі В = 16350 – 15000 = 1360

Висновок: Підрахунки рекомендують нам видати кредит, але існує ризик втратити всі гроші.

Приклад 2: Додаткові умови до попередньої задачі. Банк може перевірити платоспроможність клієнта перед тим, як видавати йому позику. Аудиторська фірма бере по 80 у.о.за кожну перевірку. Тепер банк має вирішити дві задачі:

1. проводити аудиторську перевірку чи ні;

2. видавати після цього позику чи ні.

Для вирішення першої проблеми банк перевіряє відповідність інформації, що видається аудиторською фірмою. Для цього вибирає 1000 клієнтів, які перевірялись аудиторською фірмою і яким після цього видавався кредит. Ці результати наведено у таблиці 15.

Таблиця 15. Результати аудиторської перевірки

Рекомендації аудиторської фірми	Кредит повернули	Кредит не повернули	Усього
Видати кредит	735	15	750
Не видати кредити	225	25	250
Усього	960	40	1000

Вирішувати цю задачу доцільно за схемою “дерева” рішень, яке відображає структуру проблеми.

Етапи вирішення:

1. Будуємо дерево (рис.3) та проставляємо ймовірності за даними другого етапу.

2. Використовуючи дані таблиці 15, обчислюємо ймовірності кожного наслідку:

Р(клієнт позику повертає; фірма рекомендувала) = ;

Р(клієнт позику не повертає; фірма рекомендувала) = ;

Р(клієнт позику повертає; фірма не рекомендувала) = ;

Р(клієнт позику не повертає; фірма не рекомендувала) = .

3. Зліва направо проставляємо грошові наслідки кожного із вузлів, використовуючи попередні результати. Після того, як прйдено усі квадрати рішень, вибираємо гілку, що забезпечує максимальний очікуваний дохід.

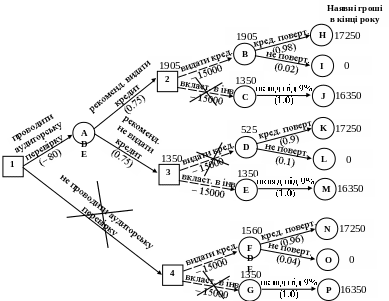
Рис. 3. Дерево рішень для банку з урахуванням аудиторської перевірки

Обчислюємо прибутки (Е) та чисті прибутки (NE) у вузлах:

Е(B) = 17250*0,98 + 0*0,02 = 16905;

NE(В) = 16905 – 15000 = 1905;

Е(С) = 16350*1 = 16350;

NE(С) = 16350 – 15000 = 1350;

Е(D) = 17250*0,9 + 0*0,1 = 15525;

NE(D) = 15525 – 15000 = 525;

Е(F) = 17250*0,96 + 0*0,4 = 16560;

NE(F) = 16560 – 15000 = 1560;

Е(G) = 16350*1 = 16350;

NE(G) = 16350 – 15000 = 1350;

Е(А) = 1905*0,75 + 1350*0,25 = 1766;

NE(А) = 1766 – 80 = 1686.

Висновок: Доцільно проводити аудиторську перевірку. Якщо фірма рекомендує видавати кредит, то кредит видавати, а якщо не рекомендує, то не видавати, а інвестувати ці гроші під стабільні 9% річних. Тобто, слід прислухатись до висновку аудиторської фірми.