Теорія корисності і її використання для пошуку рішень в умовах невизначеності і ризику. Методи шкалювання.

При вирішенні ЗПР ми застосовували відповідні критерії вибору і не враховували той факт, хто приймає рішення (з позиції матеріального статку ОПР). Теорія корисності дає можливість ОПР впливати на результат відповідно до своїх оцінок його корисності. Один і той самий критерій вибору може призвести до різних рішень у різних ОПР через те, що кожна ОПР може застосувати процес прийняття рішень до своїх запитів.

Приклад: Є 2 варіанти інвестицій 1000 у.о.:

1. 1 варіант: без ризику можна отримати 10% річних;

2. 2 варіант: подвоїти суму або ж її втратити.

Складаємо матрицю прибутків за результатами двох видів інвестицій (Табл.11).

Таблиця 11. Матриця прибутків

Наслідок Варіант рішення	Успіх	Невдача
Варіант 1	1100	1100
Варіант 2	2000	0

Для індивідуальної оцінки результату вибору вводять шкалу оцінок, наприклад, від 0 до 100 або від 0 до 1, або ж якісь інші.

За стобальною шкалою прибуток 1100 відповідає 55 балам (для 2000 – 100 балам). Для двох ОПР корисність (значимість) 1100 доларів різна.

Наприклад, для малозабезпеченої людини корисність буде високою у випадку втрати останніх грошей в разі програшу. З позицій страху втратити все, вона індивідуально оцінює ймовірність отримання 2000 доларів дуже низько, наприклад 0,1. В діапазоні значення ймовірності P = {0,1; 1} знаходиться точка заміни безризикового варіанта 1 більш прибутковим, але ризиковим варіантом 2. Значення ймовірності, де проходить зміна варіанта рішення являє собою оцінку корисності (U) 1100 доларів. Припустимо А = 0,95, тоді корисність обчислюється так: U(1100) = 0,95*100=95. Таким чином, грошова шкала 0$ – 1100$ – 2000$ заміняється шкалою 0 – 95 – 100. Це своя шкала для малозабезпеченого інвестора.

Інший інвестор володіє великим капіталом. Втрата 1000 доларів в разі невдачі для нього несуттєва. В даному випадку він із своїх позицій встановлює значення ймовірності Р, коли один варіант рішення може бути замінений іншим. Припустимо для нього Р = 0,2. Тоді при Р < 0,2 він вибирає 1 варіант рішень, а при Р > 0,2 – 2 варіант. Для нього грошова шкала 0$ – 1100$ – 2000$ заміняється шкалою 0 – 20 – 100. Таким чином, одна і та сама грошова шкала може бути замінена різними шкалами корисності залежно від можливостей та поглядів інвестора.

Використання матриці прибутків та графіка корисності при прийнятті рішень

Приклад: Припустимо Ви зібрали 5000 доларів, щоб купити квартиру. Знайомий підприємець пропонує Вам вкласти гроші в його бізнес. У випадку невдачі Ви втрачаєте 5000 $ і можливість купити квартиру. В разі успіху Ви отримаєте 30000$. Спеціаліст з маркетингу оцінує ймовірність успіху бізнесу в 0,3. Є альтернативний варіант – безризиковий – покласти гроші в банк під 9 % річних. Завдання:

1. прийняти рішення, використовуючи BL-критерій;

2. переоцінити прибутки за допомогою шкали корисності, склавши таблицю корисності та відобразивши результати на графіку корисності;

3. чи змінеться рішення після переоцінки?

Розв’язання.

1). Складаємо матрицю прибутків та проводимо розрахунки за BL-критерієм (табл. 12). (30000 * 0,3 + 0 * 0,7 = 9000; 5450 * 0,3 + 5450 * 0,7 =5450).

Табл. 12. Розрахунки за BL-критерієм

Наслідок інвестування (ймовірність) Варіант інвестування	Успіх в бізнесі	Невдача в бізнесі	BL
	0,3	0,7
1. Бізнес	30000	0	9000
2. Банк	5450	5450	5450

За грошовою шкалою вкладання грошей в бізнес приносить більший прибуток, тому що BL-критерій враховує ризик із розрахунку на великий прибуток. Але даний вибір дещо необачний через те, що в разі втрати грошей придбання квартири залишається лише мрією.

Шкала корисності для даного прикладу має вигляд:

0 балів – 0$ ; 100 балів – 30000$.

Для прибутку 5450$ не потрібна оцінка корисності, потрібно лише визначити, яка має бути ймовірність цього прибутку з точки зору ОПР, щоб вона його задовольнила. Наприклад, достатня ймовірність успіху принаймі 60%. Якщо Р = 0,6, то корисність

U(5450) = 0,6 * 100 = 60. (25)

Таблиця оцінок корисності рішень набуде вигляду (Табл. 13):

Таблиця 13. Оцінки корисності рішень

Наслідок інвестування (ймовірність) Варіант інвестування	Успіх в бізнесі	Невдача в бізнесі	BL
	0,3	0,7
1. Бізнес	100	0	0
2. Банк	60	60	60

Якщо провести розрахунки за критерієм Байєса-Лапласа, то ми приймаємо 2-й варіант рішення, що відповідає вкладанню грошей у банк. Це рішення протилежне тому, яке ми прийняли без використання шкали корисності.

Оцінити ризик можна за допомогою графіка залежності прибутку від оцінки корисності. Нанесемо значення U(0) і U(100) та з‘єднаємо їх прямою лінією. (Рис. 1).

5450

60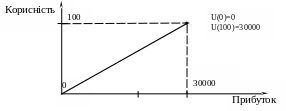

Рис.1. Графік корисності

Якщо оцінка корисності 5450$ знаходиться вище прямої, то ОПР належить до тих, хто уникає ризику. Якщо нижче, то навпаки. Із графіка видно, що в даному випадку ОПР приймає безризикове рішення.