Визначення вартості достовірної інформації.

Невизначеність при прийняті рішень можна зменшити шляхом отримання додаткової інформації, за яку потрібно заплатити. Максимальна сума грошей, яку варто заплатити, являє собою вартість достовірної інформації.

Якби заздалегідь було відомо який із варіантів буде реалізовано, то можна прийняти рішення, що забезпечить максимум прибутку, але ми не можемо контролювати результати. Очікуваний прибуток із урахування ймовірностей усіх результатів можна розрахувати таким чином:

(12)

(13)

Вартість достовірної інформації (ВДІ) являє собою різницю отриманої суми і максимально очікуваного прибутку без достовірної інформації:

ВДІ=1,86 - 1,4=0,46 (14)

Отже, отриману суму грошей фірма може платити щодня за маркетингові послуги для забезпечення реалізації продукції.

6. Прийняття рішень на основі зважених вихідних позицій. Похідні критерії вибору. Урахування ризику та ступеню довіри до вихідної інформації. Критерій Гурвиця (hw – критерій).

Критерій Гурвиця – це критерій песимізму-оптимізму, він рекомендує при оцінці альтернатив не керуватись ні крайнім легковажним оптимізмом, ні песимізмом.

Оціночна функція:

(15)

Множина оптимальних рішень за HW-критерієм формується таким чином:

(16)

де с – ваговий множник. Він означає ступінь песимізму ОПР, і вибирається нею виходячи із суб’єктивних міркувань. При с=1 критерій Гурвиця перетворюється у песимістичний ММ-критерій, а при с=0 – у критерій крайнього оптимізму.

Правило вибору рішень згідно HW-критерію:

матриця рішень || || доповнюється стовпцем із середніх виважених найменшого та найбільшого елементів кожного рядка. Вибираються ті варіанти , в рядках яких стоять найбільші значення цього стовпця.

Умови застосування HW-критерію:

1. про ймовірності появи станів нічого не відомо;

2. з появою стану необхідно рахуватись;

3. реалізується мала кількість рішень;

4. допускається незначний ризик.

Критерій Ходжа – Лемана (hl - критерій).

HL-критерій базується на мінімаксному та критерії Байєса-Лапласа і використовує ступінь довіри до розподілу ймовірностей. Якщо довіра велика, то перевага надається BL-критерію, в протилежному випадку – ММ-критерію.

Оціночна функція:

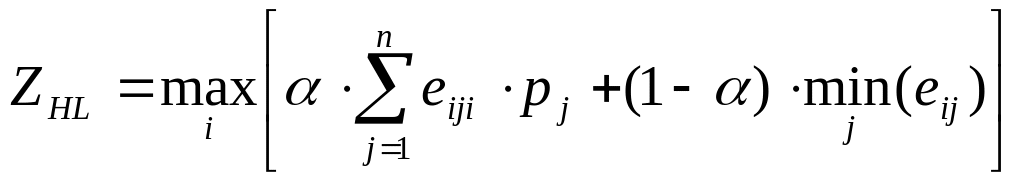(17)

Множина оптимальних рішень за HL-критерієм формується таким чином:

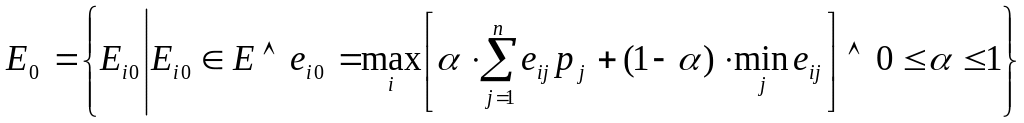(18)

Правило вибору згідно HL-критерію: матриця рішень || || доповнюється стовпцем із середніх виважених математичного очікування й найменшого елементу кожного рядка. Вибираються ті варіанти рішень, в рядках яких стоїть найбільше значення цього стовпця. При HL-критерій перетворюється в BL-критерій, а при – в ММ-критерій. Значення ОПР обирає із суб’єктивних міркувань.

Характеристики ситуації для застосування HL-критерію:

1. ймовірності виникнення зовнішніх станів невідомі, але можливі деякі припущення про їх розподіл;

2. прийняття рішення реалізується багаторазово;

3. при незначних кількостях реалізації рішення допускається деякий ризик.

Критерій Гермейєра (g-критерій) .

G-критерій базується на ММ-критерії.

Оціночна функція:

(19)

Множина оптимальних рішень формується таким чином:

(20)

Приклад: вирішити попередню задачу з використанням похідних критеріїв вибору та обґрунтувати прийняте рішення.

Доповнюємо матрицю рішень || || стовпчиком результів розрахунків за HW-критерієм для обраного вагового множника та обираємо максимальний елемент цього стовпчика, клітинку відмічаємо іншим кольором (Табл.7). При розрахунку підбираємо ваговий множник так, щоб дослідити, як він впливає на варіант рішення. При значенні с=0,6 усі рішення стають рівнозначними.

Розрахунки за HW-критерієм при с=0,55:

Для варіанта 1: 0,55 * 0,6 + (1 - 0,55) *0,6 = 0,6.

Для варіанта 2: 0,55 * 0,2 + (1 - 0,55) *1,2 = 0,65.

Для варіанта 3: 0,55 * (-0,2) + (1 - 0,55) *1,8 = 0,7.

Для варіанта 4: 0,55 * (-0,6) + (1 - 0,55) *2,4 = 0,75.

Для варіанта 5: 0,55 * (-1) + (1 - 0,55) *3 = 0,8.

Таблиця 7. Розрахунки за похідними критеріями вибору

Варіант рішення (кількість партій товару)	Можливий денний попит та ймовірність					HW		HL	G
	1 0,1	2 0,2	3 0,3	4 0,3	5 0,1	с=0,55	с=0,6
1	0,6	0,6	0,6	0,6	0,6	0,6	0,6	0,6	0,06
2	0,2	1,2	1,2	1,2	1,2	0,65	0,6	0,65	0,02
3	-0,2	0,8	1,8	1,8	1,8	0,7	0,6	0,6	-0,02
4	-0,6	0,4	1,4	2,4	2,4	0,75	0,6	0,4	-0,06
5	-1	0	1	2	3	0,8	0,6	0,05	-0,1

Доповнюємо матрицю рішень || || стовпчиком результатів розрахунків за HL-критерієм для обраного ступеню довіри до розподілу ймовірностей та обираємо максимальний елемент цього стовпчика, клітинку відмічаємо іншим кольором (Табл.7). Розрахунки за HL-критерієм для вибраного ступеню довіри до розподілу ймовірностей:

Для варіанта 1: 0,5*0,6+ (1-0,5)*0,6 =0,6.

Для варіанта 2: 0,5*0,2+(1-0.5)*1,1=0,65.

Для варіанта 3: 0,5*(-0,2)+0,5*1,4=0,6.

Для варіанта 4: 0,5*(-0,6)+ 0,5*1,4 =0,4.

Для варіанта 5: 0,5*(-1)+(1- 0,5)*1,1 = 0,05.

Доповнюємо матрицю рішень || || стовпчиком результатів розрахунків за G-критерієм та обираємо максимальний елемент цього стовпчика, клітинку відмічаємо іншим кольором (Табл. 7). Для розрахунку за G-критерієм проводяться додаткові розрахунки, наведені в таблиці 8.

Таблиця 8. Додаткова матриця для розрахунків за G-критерієм

1	0,6*0,1	0,6*0,2	0,6*0,3	0,6*0,3	0,6*0,1	0,06
2	0,2*0,1	1,2*0,2	1,2*0,3	1,2*0,3	1,2*0,1	0,02
3	-0,2*0,1	0,8*0,2	1,8*0,3	1,8*0,3	1,8*0,1	-0,02
4	-0,6*0,1	0,4*0,2	1,4*0,3	2,4*0,3	2,4*0,1	-0,06
5	(-1)*0,1	0*0,2	1*0,3	2*0,3	3*0,1	-0,1

Висновок. При вихідній позиції песимізму доцільно прийняти рішення №1, на що вказує G-критерій. За HW-критерієм ступінь песимізму у 60% робить усі рішення рівнозначними. При зменшенні цього значення варіант рішення переміщується у бік збільшення, а при збільшенні – у бік зменшення. За HL-критерієм при 50%-й довірі до розподілу ймовірностей доцільно прийняти рішення №2. Кінцеве рішення приймає ОПР, виходячи із умов прийняття рішення та власної оцінки ризику.