Критерій Лапласа (l-критерій).

L-критерій подібний до BL-критерію, але на відміну від останнього він базується не на математичному сподіванні, а на середньому арифметичному значенні наслідків усіх варіантів.

Його оціночна функція:

(6)

Множина оптимальних рішень за L-критерієм формується таким чином:

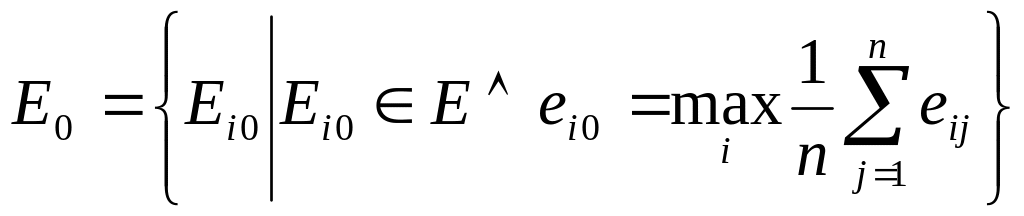(7)

Умови застосування аналогічні до умов застосування BL-критерію.

Критерій Сервіджа (s - критерій).

S-критерій базується на позиції відносного песимізму.

Оціночна функція:

(8)

Множина оптимальних рішень за S-критерієм формується таким чином:

, (9)

де (10)

Для розуміння S-критерію величину можна інтерпретувати як максимальний додатковий виграш, який досягається при виборі в стані замість варіанту іншого оптимального для цього стану. Можна і навпаки інтерпретувати величину як збитки, що виникають в стані при заміні оптимального варіанта варіантом . Тоді величина являє собою максимально можливі збитки в разі останньої інтерпретації. Тоді S-критерій мінімізує ці збитки.

Правило вибору рішення у відповідності з S-критерієм: кожен елемент матриці рішень || || віднімається від – найбільшого елемента відповідного стовпця, тобто фактично формується нова матриця залишків || ||, для якої . Дана матриця доповнюється стовпцем максимальних різниць . Вибираються ті варіанти , в рядках яких стоїть найменше значення стовпця.

Умови застосування S-критерію аналогічні умовам застосування ММ- критерію.

Приклад.

Торгівельна фірма повинна вирішити, скільки партій продукції певного виду з обмеженим терміном реалізації потрібно мати в запасі, щоб задовольнити попит клієнтів. Закупівельна ціна однієї партії продукції становить 0,7 тис. у.о., а ціна реалізації – 1,3 тис. у.о. Термін реалізації становить один день. Якщо продукцію не реалізують протягом дня, то в кінці дня її продають на внутрішньому ринку для подальшого перероблення за ціною 0,3 тис. у.о. за партію. Попит на дану продукцію за попередній період наведено у табл.2.

Таблиця 2. Попит на продукцію

Денний попит (кількість партій товару)	1	2	3	4	5
Частота попиту (кількість днів)	5	10	15	15	5

Завдання:

1. провести аналіз варіантів рішень та сформувати матрицю альтернатив;

2. вирішити ЗПР з використанням класичних критеріїв вибору та обґрунтувати вибір оптимального рішення.

Вирішення задачі.

Розраховуємо відносну частоту попиту (ймовірності), результати розрахунків подаємо у табл. 3.

Таблиця 3. Попит на продукцію, частота та ймовірність

Денний попит (кількість партій товару)	1	2	3	4	5
Частота попиту	5	10	15	15	5	∑=50
Відносна частота попиту (ймовірність)	5/50=0,1	10/50=0,2	15/50=0,3	15/50=0,3	5/50=0,1	∑=1

На основі вихідних даних формуємо матрицю альтернатив (табл.4). Елементи матриці рішень відображають прибуток, який розраховується таким чином чином:

[доходи – збитки] (11)

Таблиця 4. Матриця альтернативних рішень рішень

№ п/пор	Варіант рішення	Можливий денний попит та ймовірність
		1 0,1	2 0,2	3 0,3	4 0,3	5 0,1
1	1	1*0,6=0,6	0,6	0,6	0,6	0,6
2	2	1*0,6-1*(0,7-0,3)=0,2	2*0,6=1,2	1,2	1,2	1,2
3	3	1*0,6-2*(0,7-0,3)=-0,2	2*0,6-1*(0,7-0,3)=0,8	3*0,6=1,8	1,8	1,8
4	4	1*0,6-3*(0,7-0,3)=-0,6	2*0,6-2*(0,7-0,3)=0,4	3*0,6-1*(0,7-0,3)=1,4	4*0,6=2,4	2,4
5	5	1*0,6-4*(0,7-0,3)=-1	2*0,6-3*(0,7-0,3)=0	3*0,6-2*(0,7-0,3)=1	4*0,6-1*(0,7-0,3)=2	5*0,6=3

Проводимо розрахунки за ММ-критерієм, для цього матрицю рішень || || доповнюємо стовпцем з мінімальних значень рядків, з яких потім вибираємо максимальний, відповідну клітинку відмічаємо іншим кольором. Результати розрахунків наведено в таблиці 5.

Доповнюємо матрицю рішень || || стовпцем результатів розрахунку за BL-критерієм та вибираємо максимальний елемент цього стовпчика, клітинку відмічаємо іншим кольором (Табл. 4.). Розрахунки за BL-критерієм:

Для варіанта 1: 0,6* 0,1 + 0,6* 0,2 + 0,6* 0,3 + 0,6* 0,3 + 0,6* 0,1 =0,6.

Для варіанта 2: 0,2 * 0,1 + 1,2 * 0,2 + 1,2 * 0,3 + 1,2 * 0,3 + 1,2 * 0,1 = 1,1.

Для варіанта 3: -0,2 * 0,1 + 0,8 * 0,2 + 1,8 * 0,3 + 1,8 * 0,3 + 1,8 * 0,1 = 1,4.

Для варіанта 4: -0,6 * 0,1 + 0,4 * 0,2 + 1,4 * 0,3 + 2,4 * 0,3 + 2,4 * 0,1 = 1,4.

Для варіанта 5: -1 * 0,1 + 0 * 0,2 + 1 * 0,3 + 2 * 0,3 + 3* 0,1 = 1,1.

Таблиця 5. Результати розрахунків за класичними критеріями вибору

Варіант рішення (кількість партій товару)	Можливий денний попит та ймовірність					MM	BL	L	S
	1 0,1	2 0,2	3 0,3	4 0,3	5 0,1
1	0,6	0,6	0,6	0,6	0,6	0,6	0,6	0,6	2,4
2	0,2	1,2	1,2	1,2	1,2	0,2	1,1	1,0	1,8
3	-0,2	0,8	1,8	1,8	1,8	-0,2	1,4	1,2	1,2
4	-0,6	0,4	1,4	2,4	2,4	-0,6	1,4	1,2	1,2
5	-1	0	1	2	3	-1	1,1	1,1	1,6

Доповнюємо матрицю рішень ||e_ij|| стовпцем результатів розрахунку за L-критерієм та обираємо максимальний елемент цього стовпчика, клітинку відмічаємо іншим кольором (Табл. 5.). Розрахунки за L-критеріюєм:

Для варіанта 1: (0,6 + 0,6 + 0,6 + 0,6 + 0,6) / 5 = 0,6.

Для варіанта 2: (0,2 + 1,2 + 1,2 + 1,2 + 1,2) / 5= 1,0.

Для варіанта 3: (-0,2 + 0,8 + 1,8 + 1,8 + 1,8) / 5 = 1,2.

Для варіанта 4: (-0,6 + 0,4 + 1,4 + 2,4 + 2,4) / 5 = 1,2.

Для варіанта 5: (-1 + 0 + 1 + 2 + 3) / 5 = 1,1.

Доповнюємо матрицю рішень ||e_ij|| стовпцем результатів розрахунків за S-критерієм та обираємо мінімальний елемент цього стовпчика, клітинку відмічаємо іншим кольором. Для розрахунку за S-критерієм проводимо додаткові розрахунки, які подаємо у таблиці 6:

Таблиця 6. Додаткова матриця для розрахунку за S-критерієм

1	0,6-0,6=0	1,2-0,6=0,6	1,8-0,6=1,2	2,4-0,6=1,8	2,4-0,6=1,8	2,4
2	0,6-0,2=0,4	1,2-1,2=0	1,8-1,2=0,6	2,4-1,2=1,2	2,4-1,2=1,2	1,8
3	0,6+0,2=0,8	1,2-0,8=0,4	1,8-1,8=0	2,4-1,8=0,6	2,4-1,8=0,6	1,2
4	0,6+0,6=1,2	1,2-0,4=0,8	1,8-1,4=0,4	2,4-2,4=0	2,4-2,4=0	1,2
5	0,6-1=1,6	1,2-0=1,2	1,8-1=0,8	2,4-2=0,4	2,4-3=-0,6	1,6

За результатами розрахунків за класичними критеріями вибору робимо висновок про те, що найкращим варіантом рішення буде 3-й або 4-й варіанти, а якщо ОПР взагалі не хоче ризикувати, тоді радимо прийняти 1-й варіант рішення, на який вказує ММ-критерій.