Теорема Пифагора.
Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.
,
где a, b
– катеты, c
– гипотенуза.
! Катет всегда меньше гипотенузы.
Пифагоровы тройки: 3:4:5; 6:8:10; 5:12:13; 8:15:17.
Числовые промежутки.
(a,b) – промежуток не включает числа a и b.
[a,b] – промежуток включает числа a и b.
[a,b) – промежуток включает число a и не включает число b.
Синус, косинус, тангенс, котангенс углов 0, 30, 45, 60, 90, 180 градусов.
Синус – отношение противолежащего катета к гипотенузе.
Косинус – отношение прилежащего катета к гипотенузе.
Тангенс – отношение противолежащего катета к прилежащему.
Котангенс – отношение прилежащего катета к противолежащему.
|
0 |
30 |
45 |
60 |
90 |
180 |
Sin |
0 |
|
|
|
1 |
0 |
Cos |
1 |
|
|
|
0 |
-1 |
Tg |
0 |
|
1 |
|
- |
0 |
Ctg |
- |
|
1 |
|
0 |
- |
Основное тригонометрическое тождество.
,
.
Формулы приведения для 90 и 180 градусов.
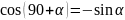
Приведение подобных слагаемых.
Подобные слагаемые – слагаемые, отличающиеся только коэффициентами, буквенная часть при этом остаётся неизменной (её может не быть).
Привести подобные слагаемые: буквенную часть вынести за скобки, а с числовыми коэффициентами произвести соответствующие арифметические действия.
Одночлен, многочлен. Действия с ними.
Одночлен – это произведение чисел, переменных и их степеней с натуральными показателями.
Не являются одночленами: дроби с переменной в знаменателе, степени с отрицательными показателями.
Для записи одночлена в стандартном виде необходимо одинаковые переменные записать с помощью степени, далее расположить множители следующим образом: коэффициент, переменные в алфавитном порядке.
Степень одночлена – сумма показателей всех переменных.
Для умножения одночленов необходимо представить их произведение в стандартном виде.
Для возведения одночлена в степень нужно возвести в эту степень каждый множитель.
Многочлен – это сумма одночленов.
Стандартный вид многочлена – запись, при которой приведены подобные слагаемые и все одночлены записаны в стандартном виде, одночлены более высокой степени расположены левее одночленов более низкой степени.
Степень многочлена – наибольшая из степеней одночленов.
! При сложении и вычитании многочленов нужно помнить: если перед скобкой стоит знак минус, то все знаки в скобках меняются на противоположные.
Для умножения многочлена на одночлен нужно каждый член многочлена умножить на этот одночлен и произведения сложить, если это возможно.
Для умножения многочлена на многочлен нужно каждый член первого многочлена умножить на каждый член второго многочлена и произведения сложить, если это возможно.