Математика. Повторение. Теория

1. Натуральные, целые, рациональные числа.

Натуральные числа – это числа, используемые при счёте. (1, 2, 3…).

Ноль не является натуральным числом.

Целые числа – это натуральные числа, им противоположные ( с минусом) и ноль.

Рациональные числа – это числа, которые можно представить в виде обыкновенной дроби.

2. Простые и составные числа.

Простые числа – это числа, которые делятся только на единицу и само себя.

Составные числа – это числа, которые имеют больше двух делителей.

1 не является ни простым, ни составным числом.

3. Деление с остатком.

a : b = c ( ост r)

a = b*c + r.

a – делимое, b – делитель, c – неполное частное, r – остаток.

4. Делители, кратные, НОД, НОК.

Делители – числа, на которые делится данное число. Например, для числа 10 делителями являются 1, 2, 5, 10.

Кратные – числа, которые делятся на данное число. Например, для числа 10 кратными являются 10, 20, 30,…

НОД (наибольший общий делитель). Для вычисления НОД нескольких чисел раскладываем числа на простые множители, находим произведение повторяющихся делителей. Например, НОД(4, 12, 18). 4 = 2 * 2, 12 = 2*2*3, 18 = 2*3*3. НОД(4, 12, 18) = 2.

НОК (наименьшее общее кратное). Для вычисления НОК нескольких чисел раскладываем числа на простые множители, находим произведение делителей первого числа, делителей второго числа, которых не было у первого числа и т.д.

Например, НОК(4, 12, 18). 4 = 2 * 2, 12 = 2*2*3, 18 = 2*3*3. НОК(4, 12, 18) =2*2*3*3 = 36.

5. Признаки делимости на 2,3,5,9,10.

Число делится на 2, если оно оканчивается на 0, 2, 4, 6, 8.

Число делится на 3, если сумма его цифр делится на 3. Например, 247: 2+4+7=13, 13 не делится на 3, значит, 247 не делится на 3. 237: 2+3+7=12, 12 делится на 3, значит, 237 делится на 3.

Число делится на 5, если оно оканчивается на 0 или 5.

Число делится на 9, если сумма его цифр делится на 9.

Число делится на 10, если оно оканчивается на 0.

6. Действия с обыкновенными дробями.

Сложение (вычитание): приводим к общему знаменателю (найти НОК знаменателей), находим дополнительные множители (разделить общий знаменатель на знаменатель каждой дроби), умножить числитель и знаменатель каждой дроби на её дополнительный множитель, числители сложить (вычесть).

Умножение: в числитель новой дроби записать произведение данных числителей, в знаменатель – произведение знаменателей; если возможно, сократить.

Деление: деление заменить умножением на дробь, обратную делителю.

7. Действия с десятичными дробями.

При сложении и вычитании запятую записываем под запятой, уравниваем количество знаков после запятой, складываем как целые числа.

При умножении вычисляем, не обращая внимания на запятые, в результате отделить запятой столько знаков справа, сколько их было после запятой во всех множителях.

При делении перенести запятую в двух числах вправо на столько знаков, сколько их после запятой в делителе. Далее делить как целые числа, когда целая часть в делимом закончится, поставить запятую в частном и продолжить деление.

8. Округление чисел.

Если за данным разрядом следует цифра от 0 до 4 включительно, то все цифры справа от данного разряда заменить нулями, а цифру данного разряда оставить без изменений. Если за данным разрядом следует цифра от 5 до 9 включительно, то все цифры справа от данного разряда заменить нулями, а цифру данного разряда увеличить на 1.

9. Нахождение части от числа, числа по его части.

При нахождении части от числа необходимо умножить число на дробь, выражающую часть.

При нахождении числа по его части – часть разделить на дробь её выражающую. Например, найти число, если две трети от него равны 6. 6 : 2/3 = 6*3/2=9.

10. Стандартный вид числа.

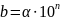, b – данное число, 1 | <10, n - целое число. Например, 3876,57 = 3, 87657 * 10³ , 0,0067475 =6,7475*10^-3 .

11. Пропорция. Основное свойство пропорции. Прямо и обратно пропорциональные величины. Деление числа пропорционально данным числам.

Пропорция – это равенство двух отношений.

Основное свойство пропорции: произведение средних членов пропорции равно произведению крайних членов.

Прямо пропорциональные величины – величины, если при увеличении (уменьшении) одной величины, вторая увеличивается (уменьшается) во столько же раз.

Например, для зависимости S = v *t расстояние и время – прямо пропорциональные величины.

Обратно пропорциональные величины – величины, если при увеличении (уменьшении) одной величины, вторая уменьшается (увеличивается) во столько же раз.

Например, для зависимости S = v *t скорость и время – обратно пропорциональные величины.

Деление числа на части пропорционально данным числам: данное число разделить на сумму чисел, выражающих части, умножить на соответствующую часть.

Например, разделить число 12 на части пропорционально числам 1 и 3. 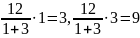. Ответ: 3 и 9. Для проверки сложить данные числа, их сумма должна быть равна исходному числу.