Тема 4. Твердое тело в механике

Вращательное движение – это движение, при котором все точки тела движутся по окружности, и центр окружности расположен на одной прямой, называемой осью вращения.

При вращательном движении положение тела в любой момент времени определяется углом поворота  радиуса-вектора R любой точки тела относительно своего начального положения [] - [рад].

У гол  - угловой путь при вращательном движении. При вращательном движении угловая скорость - . [] –

- мгновенная угловая скорость при

неравномерном движении.

- угловая скорость при равномерном

движении.

  2 - угол, соответствующий одному полному обороту тела.

t  T – соответствующее время или период обращения.

Если вращение тела происходит неравномерно, то быстроту изменения угловой скорости характеризует угловое ускорение

Направление угловой скорости определяется по правилу буравчика: направление вектора угловой скорости совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.

1)  = const,   t - равномерное движение

2)   0 - равноускоренное движение

3)  < 0 - равнозамедленное движение

- угловая скорость при равноускоренном движении.

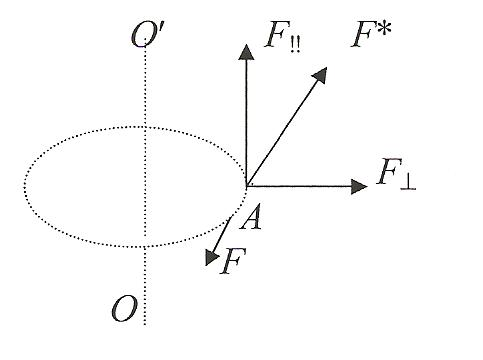
Пусть твердое тело п роизвольной формы вращается под действием силы F* вокруг неподвижной оси ОО. Все его точки описывают окружности с центрами на этой оси Разложим силу F* на три состав-ляющие: F‼, F и F (перпендикулярную силам F‼ и F).

Вращение тела вызывает только сила F, являющаяся касательной к окружности, поэтому F – вращающая сила. Действие силы F зависит не только от её значения, но и от расстояния точки её приложения А до оси вращения, т.е. зависит от момента силы.

Момент силы - произведение вращающей силы F на радиус окружности r, описываемой точкой приложения силы

M = Fr - момент силы [Hм]

Момент инерции материальной точки относительно некоторой оси - произведение массы материальной точки на квадрат расстояния до этой оси.

J = mr² - момент инерции [кгм²]

Момент инерции характеризует инертность тела при вращательном движении.

Моменты инерции разных симметричных тел массой m:

- момент инерции шара с радиусом R

- момент инерции цилиндра

- момент инерции стержня

Во всех случаях ось вращения проходит через центр масс тела.

Момент инерции относительно любой произвольной оси, не проходящей через центр масс, определяется по теореме Штейнера:

J = J₀ + md²

Момент инерции относительно любой произвольной оси, не проходящей через центр тяжести равен сумме момента инерции относительно параллельной оси, проходящей через центр тяжести и произведению массы на квадрат расстояния между этими осями.

II закон Ньютона – основной закон динамики поступательного движения

F = ma

Умножив обе стороны уравнения на r, получим:

Fr = mar

Причем, а = r, Fr = M, mr² = J

Следовательно

М = J - основное уравнение динамики вращательного движения или II закон Ньютона для вращательного движения.

У гловое ускорение

Тогда , умножив обе стороны уравнения на t полу

ч им основной закон динамики враща

тельного движения

Mt – импульс момента сил

L = J - момент импульса

Тогда аналогично закону сохранения импульса

- закон сохранения момента импульса

П ри вращательном движении кинетическая энергия определяется по формуле

Катящийся без скольжения шар совершает вращательное и поступательное движения одновременно. И полная энергия равна

W_к = W_пост + W_вращ или

Таким образом, мы выяснили, что

S,,a, t – кинематические характеристики поступательного движения

, t – кинематические характеристики вращательного движения

F, m, p - динамические характеристики поступательного движения

M, J, L - динамические характеристики вращательного движения