Контрольные вопросы

1. Что характеризуют вектора магнитной индукции и напряженности

магнитного поля и какова зависимость между ними?

2. Применить правило буравчика для определения направления магнитных

полей прямого и кругового тока.

3. Сформулировать и записать закон Био-Савара-Лапласа.

4. Вывести напряженность магнитного поля прямого тока конечных разме

ров.

5. Вывести напряженность магнитного поля на оси и в центре кругового

тока.

Л а б о р а т о р н а я р а б о т а № 30

Исследование процесса разряда конденсатора через сопротивление

Ц е л ь р а б о т ы: определение постоянной времени цепи.

П р и б о р ы: экспериментальная установка.

Т е о р и я м е т о д а

Всякий, даже “мгновенный” процесс на самом деле длится некоторое время, хотя быть может и очень короткое. Изучение переходных процессов, т.е. установление того или иного явления стационарного течения процессов, позволяет часто глубже вскрыть природу и ход самого явления, понять его, а следовательно и использовать на практике. В области электрических явлений особый интерес представляют переходные процессы при заряде и разряде конденсатора.

Зарядка конденсатора начинается с момента присоединения конденсатора к источнику постоянного тока (схема 1) и длится до момента полного заряда конденсатора т.е. до возникновения разности потенциалов на пластинах конденсатора равной э.д.с. источника. При этом, очевидно, на конденсаторе появится напряжение U, направленное противоположно э.д.с. источника e₁. Рост напряжения на конденсаторе по мере накопления зарядов на его обкладках вызывает уменьшение зарядного тока, определяемого формулой

т.к. действующее значение напряжения, равное в каждый момент разности e- U убывает.

В момент полного заряда конден-

сатора, когда U станет равным e,

действующее напряжение окажется

равным нулю и тогда ток заряда

прекратится. Теоретически это

наступит через бесконечно боль-

Схема I. шое время, а практически, если конденсатор заряжается через малое сопротивление, почти мгновенно. Такое убывание тока от максимального до нуля наблюдается при разряде конденсатора, так как ток пропорционален изменению заряда в единицу времени (1), величина заряда пропорциональна емкости конденсатора dq =с dU, то (2)

По закону Ома (3)

Тогда из уравнений (2) и (3) получим

или (4)

Формула (4) показывает, что относительный спад напряжения на конденсаторе пропорционален протекшему времени и обратно пропорционален произведению R× с. Следовательно, спад напряжения на конденсаторе происходит тем медленнее, чем больше R и чем больше с, составляющие разрядную цепь. Важным параметром, характеризующим цепь из последовательно соединенных сопротивлений и емкости, является произведение R× с, которое называется постоянной времени цепи. Если взять интегралы от обеих частей уравнения

(5)

знак «минус» указывает на убыль напряжения, то можно определить закон изменения тока при разряде конденсатора

;

;

С учетом того, что e = I₀R, I =

имеем I= =I

где I - сила тока к моменту времени, Iо - максимальная сила тока при R - сопротивление, с - емкость, t - время, е - основание натурального логарифма.

Обозначим Rс = - постоянная времени цепи. Если = t, то

I=I = = 0,37 I

Постоянная времени цепи показывает, что через Rс секунд сила тока убывает в 2,7 раза, или составляет от максимального значения 0,37Iо (рис. 1).

В задачу настоящей работы входит:

изменение силы разрядного тока через различные промежутки времени.

Определение по этой кривой постоянной времени и сравнение t

полученной величины с результатом

расчета по формуле = Rс

рис.1

П о р я д о к р а б о т ы

1 . Собрать схему 2.

секундомер

Схема 2.

В нее входит конденсатор с, большое сопротивление R, которое определяет величину начального зарядного тока, микроамперметр, ключ К и источник e. При работе с электрическими конденсаторами в несколько десятков или сотен микрофарад можно применять стрелочные приборы типа М-24 на 50-100 мкА, при очень больших применяется зеркальный гальванометр.

2. Записать максимальное отклонение стрелки гальванометра nо в делениях. Оно пропорционально току заряда конденсатора Iо, величина которого определяется только э.д.с. источника тока и зарядным сопротивлением R.

3. Нажать кнопку ключа и не отпускать, одновременно с этим включается секундомер и в процессе разряда конденсатора записать значения амперметра спустя 3с, 6с, 9с, 12с и т.д.

4. Опыт повторить 3 раза.

Показания записать в таблицу:

Таблица

t	0	3	6	9	12	15	18	21	24	27	30
I
I
I

5. По полученным данным построить график, выражающий

зависимость: I= f (t)

6. Определить по графику величину постоянной времени цепи соответствующую моменту времени, при котором I = 0,37Iо пользуясь методом, приведенным на рис. 1 .

7.Сравнить найденную величину с вычисленной по формуле:

К о н т р о л ь н ы е в о п р о с ы

1. Что такое электроемкость и единицы ее измерения?

2. Что представляет собой простейший конденсатор? Записать емкость

плоского, сферического и цилиндрического конденсаторов

3. Емкость конденсатора с многослойным диэлектриком.

4. Каков физический смысл постоянной времени цепи?

5. Получить закон изменения тока при разряде конденсатора.

Лабораторная работа № 39

ИЗУЧЕНИЕ ПОСЛЕДОВАТЕЛЬНОЙ ЦЕПИ

ПЕРЕМЕННОГО ТОКА

Цель работы: изучение законов переменного тока, определение индуктивности, емкости и полного сопротивления цепи

Приборы: амперметр, вольтметр, реостат, катушка индуктивности, конденсатор, соединительные провода.

Теория метода

Основными параметрами электрической цепи являются напряжение U, сила тока I и сопротивление R. Эти параметры связаны по закону Ома

Если на сопротивлении R выделяется мощность, то оно называется активным. В цепях переменного тока имеются реактивные сопротивления, т.е. безваттные, не поглощающие энергию. Это катушка индуктивности L и конденсатор емкостью c.

Если на активное сопротивление подать переменное напряжение, изменяющееся по закону синуса U=U₀ sinωt, то и сила тока также будет изменяться по закону синуса:

,

где U₀ и I₀ – амплитудные значения напряжения и силы тока.

Напряжение и ток совпадают по фазе (диаграмма 1)

диаграмма 1

Если цепь содержит катушку индуктивности, то при прохождении переменного тока в ней возникает ЭДС самоиндукции

пропорциональная изменению силы тока в единицу времени, где коэффициентом пропорциональности является индуктивность L.

ЭДС самоиндукции уравновешивается с напряжением на катушке

Обозначив ωLI₀=U₀, где U₀ – амплитудное значение напряжения, т.е. напряжение на катушке опережает ток на (диаграмма 2)

Амплитудное значение силы тока равно

где ωL представляет индуктивное сопротивление R_L.

Если цепь содержит конденсатор емкостью с, то напряжение на нем будет равно и сила тока равна изменению заряда в единицу времени

Заряд пропорционален напряжению, тогда сила тока будет равна

Обозначим , получим .

Следовательно, напряжение на конденсаторе отстает по фазе от тока на (диаграмма 3).

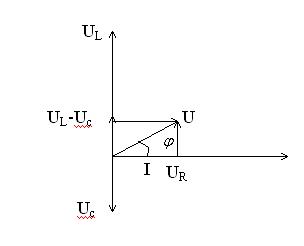
диаграмма 3 диаграмма 4

Амплитудное значение тока можно представить как ,

где знаменатель выражает емкостное сопротивление R_c.

Если цепь содержит активное сопротивление R, то общее напряжение будет равно векторной сумме напряжений U_R, U_L, U_c (диаграмма 4).

Полное сопротивление цепи или

Введя индуктивное и емкостное сопротивление, получим:

Ток и напряжение сдвинуты по фазе на угол φ.

Из диаграммы 4 определим тангенс угла φ

П о р я д о к р а б о т ы

Упражнение 1. Определение индуктивности катушки

1. Собрать цепь по схеме 1.

2. Измерить ток и напряжение на клеммах катушки.

3. Вычислить сопротивление R_z и индуктивность L катушки по формуле:

где - полное сопротивление

4. Опыт повторить три раза.

схема 1 5. Внести в катушку магнитный сердечник

и повторить измерения и расчеты.

6. Данные занести в таблицу 1. Сопротивление катушки R = 18,5 Ом

Таблица 1

№ п/п	без сердечника					с сердечником
	U,В	I,А	RZ,Ом	<RZ>,Ом	L,Гн	U,В	I,А	RZ,Ом	<RZ>,Ом	L,Гн
1 2 3

Упражнение 2. Определение электроемкости конденсатора

1 . Собрать цепь по схеме 2.

2. Измерить силу тока и напряжение на конденсаторе и вычислить полное сопротивление

3. Рассчитать электроемкость конденсато- ра по формуле:

схема 2

4. Опыт повторить три раза и данные занести в таблицу 2.

Таблица 2

№ п/п	U,В	I,А	RZ,, Ом	<Rz>,Ом
1 2 3

Упражнение 3. Определение полного сопротивления цепи

1. Собрать цепь по схеме 3.

2. Измерить силу тока и напряжение.

3. Вычислить полное сопротивление цепи

по формуле .

4. Произвести расчет по формуле

схема 3 и сравнить результаты.

5. Опыт повторить три раза.

6. Затем внести в катушку сердечник, повторить измерения и расчеты.

7. Данные занести в таблицу 3

Таблица 3

№ п/п	без сердечника					с сердечником
	U,В	I,А	RZ,Ом	<RZ>,Ом	L,Гн	U,В	I,А	RZ,Ом	<RZ>,Ом	L,Гн
1 2 3

К о н т р о л ь н ы е в о п р о с ы

1. Какое сопротивление называется активным, реактивным?

2. Как влияют емкостное и индуктивное сопротивление на колебания тока

и напряжения?

3. Вывод формулы индуктивного и емкостного сопротивления.

4. Вывести формулу полного сопротивления, используя векторную

диаграмму.

5. Как изменится ток в цепи при удалении сердечника из катушки?